Peeling back the layers or doubling the stakes?

Francisco Guinea

Viewpoint

Peeling back the layers or doubling the stakes?

Francisco Guinea

Instituto de Ciencia de Materiales de Madrid, Madrid, Spain

January 4, 2010• Physics 3, 1

Calculations of bilayer graphene reveal the possibility of new electronic phases.

Figure caption — **Figure 1:** (Top left) Atomic arrangement in bilayer graphene, with the two main hopping parameters, $γ_{0}$ and $γ_{1}$ , between carbon $π$ orbitals within and between layers, respectively. (Top right) Electronic bands of bilayer graphene. Single-layer graphene features Dirac cones with sharp neutrality points, whereas bilayer graphene exhibits parabolic dispersion as shown. There are two valence and conduction bands, as each layer contributes with one set of bands. (Bottom) Feynman diagrams, such as the example shown, are used to calculate the electron-hole polarizability. This diagram depicts the dynamics of an electron-hole pair, obtained from the convolution of electron (red) and hole (blue) propagators. The calculation gives gives a logarithmically divergent polarizability.

In the years since its highly unusual properties began to emerge, graphene [1] has become an exciting research topic. Among other features, the unusual electronic band structure of single-layer graphene, with its vanishing effective carrier mass, implies that the low-energy carriers behave differently from electrons in typical metals. Some features are similar to those of elementary particles in high-energy physics. A vanishing effective mass means that the density of states at the neutrality point (that is, the point at which the valence and conduction bands meet) and the compressibility of the electron gas are also zero. As a result, unlike in other condensed matter systems, the long range Coulomb interaction is only partially screened, leading to unusually short electronic lifetimes [2] and to logarithmic divergences, like those found in quantum electrodynamics when a perturbative analysis is used. Note that here the ratio of the electronic charge to the Fermi energy $e^{2} / v_{F}$ plays the same role as the fine structure constant in QED (however, in graphene this ratio is approximately equal to $1$ ).

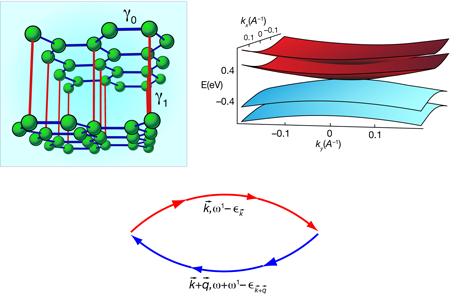
Bilayers of graphene (top left panel of Fig. 1) are also now the subject of intense interest. They have an electronic dispersion (shown in the top right panel) that is rather different from that in a single-layer system. In this case, the carriers do have an effective mass, and, in the simplest approximation, the Fermi energy at the neutrality point coincides with the touching point of the (quadratic) electron and hole bands [3]. There is a finite screening length, but electrons at the bottom of a two-dimensional parabolic band have unusual features. Short-range interactions lead to logarithmic divergences as in the single-layer case.

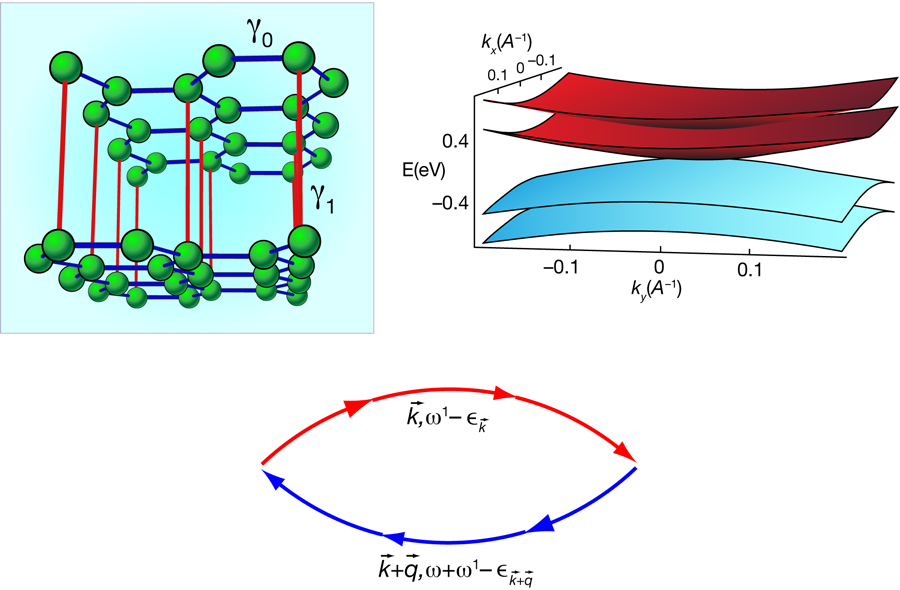
We are also learning that bilayer graphene resembles the one-dimensional “Luttinger liquid,” with metallic features but no well-defined quasiparticles (the simplest approximation shows that the inverse lifetime has the same behavior as the energy of the quasiparticle itself [4]). Now, writing in Physical Review B, two groups—one with Fan Zhang, Hongki Min, Allan MacDonald (University of Texas, Austin), and Marco Polini (Scuola Normale Superiore, Pisa, Italy) [5] and the other with Oskar Vafek and Kun Yang (Florida State University, US) [6]—have carried out a renormalization group analysis [7] in order to identify the leading instabilities of the electron gas. Such instabilities would open the door to new and interesting phase transitions. While the Feynman diagrams to be calculated are very similar in the 1D Luttinger liquid and in bilayer graphene (bottom panel of Fig. 1), they compensate each other in a different way [5]. The dimensionless coupling that determines the strength of the interaction effects is ( $U a^{2} m_{eff}) / (ħ^{2}$ ), where $U$ is an energy scale related to the local interactions, $a$ is the lattice constant, and $m_{eff}$ is the effective mass.

Although the two papers use similar techniques, the choice of possible interactions is not the same, leading to different broken symmetry phases at low temperatures: Zhang et al. [5] find a ferroelectric phase where charge is transferred between layers, driven by the interlayer interactions, in agreement with previous calculations [8]. Vafek and Yang observe in their calculations an electronic nematic phase, where the order parameter takes a preferred direction, as in a liquid crystal, and the quadratic dispersion is changed into two Dirac bands [6]. The phase is induced by interactions between electrons at atoms in different layers, and the order parameter is the line connecting the two Dirac points.

The formation of a ferroelectric phase has an electrostatic energy cost [9], which also shows a logarithmic (squared) dependence. The ferroelectric phase, like the formation of excitonic condensates in other bilayer systems, is driven by the exchange energy. A careful consideration of the full exchange interaction [8,10] shows that it can overcome the electrostatic contribution. It is worth mentioning that local interactions like the Hubbard intra-atomic repulsion, can lead to phases not considered in these works, such as antiferromagnetic ordering between the layers [11]. The analysis done so far does not fully address the relevant perturbations such as deviations from perfect isotropy and inhomogeneities. Numerical estimates suggest that the strength of the instabilities is large enough to lead to consequences that can be observed with current experimental techniques.

Understanding the role of electron-electron interactions in bilayer graphene is a challenging problem, whose theoretical analysis requires sophisticated tools. The progress made by Zhang et al. and by Vafek and Yang is remarkable, although a lot of work is still to be done. Bilayer graphene shares many features with three-dimensional graphite, making a detailed analysis of electron-electron interactions in this system even more interesting.

References

K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva, and A. A. Firsov, Science 306, 666 (2004)
J. González, F. Guinea, and M. A. H. Vozmediano, Phys. Rev. Lett. 77 3589 (1996)
E. McCann and V. I. Fal’ko, Phys. Rev. Lett. 96, 086805 (2006)
Y. Barlas and K. Yang, Phys. Rev. B 80, 161408 (2009)
F. Zhang, H. Min, M. Polini, and A. H. MacDonald, Phys. Rev. B 81, 041402 (2010)
O. Vafek and K. Yang, Phys. Rev. B 81, 041401 (2010)
R. Shankar, Rev. Mod. Phys. 66, 129 (1994)
H. Min, G. Borghi, M. Polini, and A. H. MacDonald, Phys. Rev. B 77, 041407 (2008)
E. McCann, D. S. L. Abergel, and V. I. Fal’ko, Solid State Commun. 143, 110 (2007)
R. Nandkishore, and L. Levitov, arXiv:0907.5395 (2009)
J. Nilsson, A. H. Castro Neto, N. M. R. Peres, and F. Guinea, Phys. Rev. B 73, 214418 (2006)

About the Author

Francisco (Paco) Guinea is senior researcher at Consejo Superior de Investigaciones Científicas (CSIC), the organization that coordinates many public research labs in Spain. He graduated from the Universidad Autónoma, Madrid, Spain, in 1980. Since then he has had great fun working on many topics in condensed matter theory. He finds the problems at the interface between mesoscopic physics, many body theory, and statistical mechanics, particularly challenging and interesting, with graphene being an excellent example.