Textbook physics from a cutting-edge material

Michael S. Fuhrer

Viewpoint

Textbook physics from a cutting-edge material

Michael S. Fuhrer

December 13, 2010• Physics 3, 106

Tuning the area of the Fermi surface of graphene demonstrates the fundamental physics of electron-phonon scattering.

Figure caption — **Figure 1:** Illustration of high-temperature and low-temperature electron-phonon scattering behavior in metals. (a)–(c) Typical metal with large Fermi surface. (a) At temperatures greater than or equal to the Debye temperature $T \geq θ_{D}$ , all phonon modes are excited (shaded area) up to the maximum phonon wave vector in the crystal $q_{D} = k_{B} θ_{D} / ħ v_{s}$ . Electron-phonon scattering processes (black arrows) scatter electrons from one point on the Fermi surface (blue circle) to another. (b)–(c) As the temperature is reduced below the Debye temperature $T < θ_{D}$ , only phonons with a maximum wave vector $q_{max} = k_{B} T / ħ v_{s}$ are excited (shaded area). In this Bloch-Grüneisen regime, the area of the Fermi surface available for scattering shrinks as $q_{max}^{2} \sim T^{2}$ in three dimensions ( $q_{max} \sim T$ in two dimensions), and as the allowed scattering angle becomes small, the momentum lost by a scattering event decreases as $Δ q_{| |, max} \sim q_{max}^{2} \sim T^{2}$ . The electron-phonon coupling constant is also proportional to $q$ , leading to an additional factor of $T$ in the resistivity $ρ$ , and the result is that in the Bloch-Grüneisen regime $ρ (T) \sim T^{5}$ in three dimensions, and $ρ (T) \sim T^{4}$ in two dimensions. (d)–(f) Behavior for small Fermi-surface metal (e.g., graphene). (d) For $T \geq θ_{D}$ , all electron-phonon scattering events on the Fermi surface are possible. (e) At the Bloch-Grüneisen temperature $T = T_{BG}$ , the maximum phonon wave vector $q_{max} = k_{B} T_{BG} / ħ v_{s}$ just spans the Fermi surface, i.e., $q_{max} = 2 k_{F}$ , and all electron-phonon scattering events are still allowed. (f) Only for temperatures $T < T_{BG}$ do the typical excited phonons (shaded area) lack enough momentum to span the Fermi surface, the phase space for electron-phonon scattering on the Fermi surface becomes restricted, and the low-temperature Bloch-Grüneisen regime is entered.

Graphene has garnered significant attention for its unusual massless electronic dispersion and the ability to realize exotic electronic phenomena such as the integer [1,2] and fractional [3,4] quantum Hall effects in a new condensed matter system. However, graphene is also a conceptually simple two-dimensional electronic system, which makes it ideal as a testbed to demonstrate textbook condensed matter phenomena. In a recent publication in Physical Review Letters, Dmitri Efetov and Philip Kim at Columbia University, US, do just that, studying the temperature-dependent scattering of electrons by phonons in graphene [5]. They demonstrate that the boundary between high-temperature and low-temperature behavior in the electron-phonon scattering is set not by the Debye temperature—the characteristic phonon energy scale—as in conventional metals with large Fermi surfaces, but rather by the Bloch-Grüneisen temperature, a characteristic electronic energy scale for metals with small Fermi surfaces, such as graphene [6] and doped semiconductors [7]. Efetov and Kim demonstrate tuning of the Bloch-Grüneisen temperature by almost an order of magnitude by varying the Fermi energy in graphene over a wide range of more than $\pm 1 eV$ by applying a voltage to a gate.

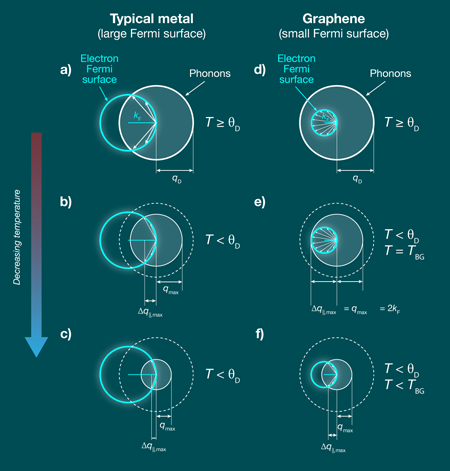
The resistivity of metals due to electron-phonon scattering is a basic problem in condensed matter physics. Scattering of electrons by phonons at finite temperature is an unavoidable phenomenon, and this “intrinsic resistivity” is typically the dominant source of resistivity in metals at room temperature. The familiar result is that at high temperature the resistivity of a metal $ρ$ is proportional to temperature $T$ . This reflects the bosonic nature of the phonons that scatter the electrons: at temperatures greater than the Debye temperature $θ_{D}$ , the characteristic temperature at which all phonon modes of a crystal are excited, the phonon population in any given mode is proportional to $T$ , hence the number of scatterers and the resistivity are proportional to $T$ . Below the Debye temperature, the phonon modes begin to “freeze out,” and in a typical metal the resistivity drops much more rapidly. For a three-dimensional metal, the resistivity is expected to drop as $ρ (T) \sim T^{5}$ ( $T^{4}$ for a two-dimensional metal), the so-called Bloch-Grüneisen regime [8,9]. Figure 1 illustrates this effect and the factors that lead to the $T^{5}$ or $T^{4}$ dependences.

What about graphene? Graphene is a strikingly different condensed matter system compared to conventional metals and semiconductors: in graphene, electrons obey the Dirac equation for massless relativistic Fermions, with a “pseudospin” degree of freedom playing the role of the relativistic spin [10]. But graphene is also a conceptually simple material: it has strictly two-dimensional electrons and phonons, and, to very good approximation, the dispersion of the electronic bands $E = ħ ν_{F} | k |$ is described by a single parameter, the Fermi velocity $ν_{F} = 1.1 \times 10^{6} m / s$ . Graphene is also amazingly tunable: the Fermi energy in a given piece of graphene can be widely tuned by chemical doping [11,12] or an electrostatically coupled gate electrode [13], and the dielectric constant (and the strength of electron-electron interactions) can be tuned by changing the dielectric substrate on which the graphene sits [14], all while maintaining essentially the same two-dimensional dispersion relation.

The combination of simplicity and tunability makes graphene ideal for experiments that illustrate fundamental condensed matter phenomena. It was shown as early as 1980 that the simple band structure of graphene leads to a particularly simple result for the electron-phonon resistivity in the high-temperature $[ρ (T) \sim T]$ limit [15]. Notably, the high-temperature resistivity is independent of Fermi energy (and hence carrier density), explaining the experimentally observed nearly constant resistivity in intercalated graphite compounds, even when carrier density varied over more than an order of magnitude [16]. More recently, a resistivity linear in temperature but independent of carrier density was observed in graphene devices where carrier density could be tuned by a gate [17]. The resistivity is also extremely small; at room temperature the intrinsic two-dimensional resistivity is only about $30 Ω$ [17], corresponding to a three-dimensional resistivity of about $1 μ Ω cm$ , lower than silver (the material with the lowest known intrinsic resistivity at room temperature). Coupled with graphene’s high transparency [18], the low intrinsic resistivity may make graphene the ultimate transparent conducting electrode material.

Graphene is an extraordinarily stiff material, leading to an unusually high Debye temperature of $\sim 2800 K$ , much higher than the temperature in the experiments of [5] and [17]. Why is the high-temperature resistivity behavior $ρ (T) \sim T$ observed at all? The answer is that in most metals, the Fermi surface is large, such that all phonons in the material have $q \leq 2 k_{F}$ and are able to scatter electrons. In graphene, the Fermi surface is very small, and only a small portion of the phonons have $q \leq 2 k_{F}$ and can scatter electrons. This collection of small- $q$ phonons has a smaller characteristic temperature; they are all populated above the Bloch-Grüneisen temperature $θ_{BG} = ħ ν_{s} k_{F} / k_{B} < θ_{D}$ , leading to high-temperature behavior $ρ (T) \sim T$ persisting down to $T = θ_{BG} < θ_{D}$ . Uniquely in graphene, both the electron energy and the phonon energy are linear in wave vector, so the Bloch-Grüneisen temperature has a particularly simple form $θ_{BG} = (2 ν_{s} / ν_{F}) T_{F}$ , where $T_{F} = E_{F} / k_{B}$ is the Fermi temperature. Thus the Bloch-Grüneisen temperature is an electronic energy scale, simply proportional to the Fermi temperature, but downscaled appropriately by twice the ratio of the sound velocity to the electron velocity, about $2 %$ in the case of graphene.

The above reasoning leads to a prediction that had never before been tested: the Bloch-Grüneisen temperature $θ_{BG}$ is tunable with Fermi energy. In graphene, $E_{F}$ can be widely tuned by chemical doping or gating and yet remains strictly two-dimensional—there are no higher-energy subbands in play as would be the case in a two-dimensional quantum well in a semiconductor heterostructure. Efetov and Kim used an electrolytic gate to tune the Fermi energy in graphene over a very wide range, exceeding $\pm 1 eV$ . They carefully measured the temperature-dependent resistivity at various Fermi energies and confirmed that they had tuned the Bloch-Grüneisen temperature over almost an order of magnitude, from $100$ to $900 K$ , observing the proportionality $θ_{BG} \sim E_{F}$ . At high temperature, they observed $ρ (T) \sim T$ with a magnitude independent of Fermi energy, confirming theoretical expectations [6]. In the low-temperature regime, they observed $ρ (T) \sim T^{4}$ , as expected theoretically for two-dimensional graphene [6].

The experiment of Efetov and Kim will undoubtedly be used as a textbook illustration of electron-phonon scattering in metals. It was enabled by some under-appreciated aspects of graphene: the simplicity of its dispersion relation, the strict two-dimensional confinement of electrons, and the ability to effect wide changes in Fermi energy with a gate. Other phenomena predicted long ago are waiting to be demonstrated with this new material.

References

K. S. Novoselov et al., Nature 438, 197 (2005)
Y. Zhang et al., Nature 438, 201 (2005)
X. Du et al., Nature 462, 192 (2009)
K. I. Bolotin et al., Nature 462, 196 (2009)
D. K. Efetov and P. Kim, Phys. Rev. Lett. 105, 256805 (2010)
E. H. Hwang and S. Das Sarma, Phys. Rev. B 77, 115449 (2008)
H. L. Stormer et al., Phys. Rev. B 41, 1278 (1990)
F. Bloch, Zeitschrift für Physik 59, 208 (1930)
E. Gruneisen, Ann. Phys. (Leipzig) 16, 530 (1933)
M. S. Fuhrer, C. N. Lau, and A. H. MacDonald, MRS Bulletin 35, 289 (2010)
F. Schedin et al., Nature Mater. 6, 652 (2007)
J. H. Chen et al., Nature Phys. 4, 377 (2008)
Y.-J. Yu et al., Nano Lett. 9, 3430 (2009)
C. Jang et al., Phys. Rev. Lett. 101, 146805 (2008)
L. Pietronero et al., Phys. Rev. B 22, 904 (1980)
M. S. Dresselhaus and G. Dresselhaus, Adv. Phys. 30, 139 (1981)
J. H. Chen et al., Nature Nanotech. 3, 206 (2008)
R. R. Nair et al., Science 320, 1308 (2008)

About the Author

Michael S. Fuhrer is a Professor in the School of Physics and Astronomy at Monash University, is an Australian Research Council Laureate Fellow, and is the director of the Monash Centre for Atomically Thin Materials. Fuhrer received his Ph.D. in physics from the University of California, Berkeley, in 1998. Prior to his current position, he was on the faculty of the University of Maryland, where he directed the Center for Nanophysics and Advanced Materials. Fuhrer’s research focuses on the electronic properties of low-dimensional materials, such as carbon nanotubes, graphene, and the surface and edge states of topological materials. He is a fellow of the American Physical Society and the American Association for the Advancement of Science.