Rewiring for adaptation

Epidemics of contagious diseases have the potential to wipe out entire populations. While medicine is making enormous advances in finding ways to treat and cure many of these diseases, it is perhaps equally important to develop ways to curtail their spread by disrupting infectious contacts. Effective vaccine distribution, particularly when resources are scarce, as well as educating groups and individuals on how to react to the presence of a disease threat, can radically diminish the chance of a disease epidemic.

In this respect, epidemic models can be enormously helpful in understanding the rate at which diseases spread and how to control them. For these models to be most effective, however, they have to be able to take into account that individuals and groups will adapt their behavior as they gain more information. This is an increasingly relevant factor as radio, television, and the internet speed up the rate at which people learn about a disease threat and how best to avoid catching and spreading it further. If the latest scare over the $\text{H}1\text{N}1$ (swine flu) virus is any indication, people appear to be more conscious than ever of epidemics. Whether the information that is delivered by the media is accurate is in itself an important issue, but regardless, it is clear that in many cases, people will attempt to reduce their chances of infection by taking actions to eliminate contact with contagious individuals, or through available vaccination. This sort of social adaptation on the level of an individual can change the dynamics of the social contact network, which in turn alters the progression of disease.

Behavioral epidemiology is defined here to be the study of the effects of social response to the threat of disease. In this article, we will discuss recent progress in designing network models that can account for “adaptive behavior” and tackle the problem of the spread of infectious diseases in a dynamic population. We start by giving an overview of simpler models, where the population is assumed to be homogeneous, and show how to progressively make these models more complex and realistic: first by considering that distinct demographics may behave differently, then that interactions along particular “links” in the network may change with time, and ultimately, allowing the network itself to “rewire” to reflect the way humans modify their social contact behavior.

These networks are designed to model the real-world problem of disease spread, but at their roots are the computational tools developed in the fields of mathematical biology and statistical physics. The spread of an epidemic is often assumed to be a stochastic process, and just as in a many-body statistical system, it is possible to find phase transitions. (As an example, the phase transition, or “threshold,” at which diseases begin to spread across the entire network is often approached via percolation theory.) For this reason, epidemiological models rely on progress in solving problems in statistical physics and, since the models can be tested against real observations from data, also provide important feedback on these physics ideas.

Our understanding of how infectious disease epidemics evolve in populations has a long and varied history that dates back to the eighteenth century [1]. Two important modern developments have helped refine our understanding of disease propagation and the occurrence of disease outbreaks: the invention of high speed computing, which can analyze data on large spatial geographic scales as well as demographic data, and progress in designing models that more truly reflect human behavior.

Deterministic mathematical models have been used since the time of Bernoulli [2] to understand the spread of infectious diseases such as smallpox in large, uniform populations. These early epidemic models assumed that the population was homogeneous, meaning it was well mixed spatially. In this sense, since all individuals behaved like the average, the models could be considered “mean-field.” Models based on mean-field dynamics describe infectious transmission from one individual to another via nonlinear mass action terms [3], where a susceptible (S) individual comes into contact with an infectious (I) individual. Models are named according to how individuals “flow” within them, such as SIS, in which susceptibles become infected and then again susceptible, or SIR, where recovered or removed (R) individuals are immune. Despite their simplicity, these models were able to predict outbreaks of childhood diseases [4]. In general, however, deterministic models on uniform populations are not sufficient to account for some of the important stochastic dynamics that occur in finite populations. These include extinction, where the infectious population vanishes (as with smallpox) [5–7], and sustained fluctuations or oscillations [8], where oscillations having random amplitude persist in small populations. This is often the case for childhood diseases.

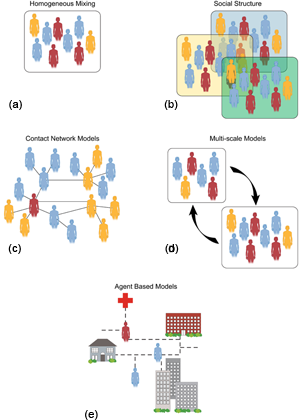
Allowing for populations to have some spatial or demographic structure is necessary to explain other observed dynamical phenomena, such as traveling waves in single [9] and multistrain [10] diseases, and recurrent outbreaks in network models [11]. There are different approaches to relaxing the assumption that the population is well mixed and homogeneous, all of which can be applied on a variety of length scales [12]. For example, a population can be broken down by age, gender, or social action. This may come into play, for example, when in order to model the transmission of HIV, one considers common characteristics of people who share needles [13]. The simplest way to handle this spatial structure is to decompose the population into subpopulations, each of which is connected to a subset of the others (see Fig.1). These connections can be through migration, as when people in one subpopulation are transported into another by air travel [14]. Although these models are “coarse grained,” meaning they still average over portions of the population, they do yield significantly different epidemic dynamics than homogeneous populations. For example, they can predict small amplitude, long-period outbreaks in a given subpopulation [15], as well as fluctuations.

Illustration: Carin Cain, after Ref. [12]

Illustration: Carin Cain, after Ref. [12]

×

At a much finer level, what are called agent-based models describe the detailed characteristics of each individual and how he or she affects the population. The scale of the population in this type of epidemic model may be as large as a city or as small as a classroom [16]. As a subset of agent-based models, contact network models provide detailed network structure among individuals [17] and may describe the effect of movement among individuals. The connections between individuals at this level of detail may change in time as a result of individual motion and decisions.

These large-scale descriptions of individuals through contact and/or agent-based models rely on sizeable databases of social interaction, and may be considered social computing models. These models are extremely valuable when studying the effects of changes to parameters, such as when to change a vaccine policy or how much to increase the length of a school closing [18]. Analyzing the full social computing agent-based models is, in general, quite difficult because of their large size and the required computational complexity. For contact models on a social network, however, some tools have been developed to understand the population structure, such as community structure to reveal shared common traits within a population network [19] and scaling laws to predict epidemic rate of spread [20].

In almost all of these network models, the epidemic propagates on a fixed, or static, network. The advantage of this is that it is possible to figure out the threshold for an epidemic to occur given the average properties of the network, such as the number of connections coming out of each node (i.e., the node “degree”). A few of the network models predict oscillations and fluctuations due to random transitions on the network. Fluctuations of simple epidemic models have been simulated on large networks [21–25].

The epidemic dynamics are typically studied as an SIS or SIR model, in which the population is large and isolated. Controls based on vaccination have been considered as well [26,27] to control the size of the outbreak. Although most of the epidemic models have fixed network structure, several recent models have considered epidemics on a network that changes structure dynamically according to rules that do not depend on the epidemic status at a node [28,29]. That is, the contact structure is time dependent but does not depend on the infection status of the individuals in the system. We will next consider networks that adapt to the state of the system as one of the new trends in epidemic modeling.

In general, many of the network models describing outbreaks consider networks where the links and contact structure don’t change with time. Yet in the presence of a natural or man-made biological threat, it is highly probable that people will change their behavior. Such an assumption holds if the population of healthy, or susceptible, individuals knows the existence of infectious individuals and adapts their behavior to avoid contact with disease [30]. More frequent hand washing, wearing a mask when contagious, and self-imposed isolation are all examples of adaptive behavior in the presence of a disease. The implication is that not only does the disease status of individuals change in time, but so do the contacts. In fact, the change in disease status causes a change in contact behavior.

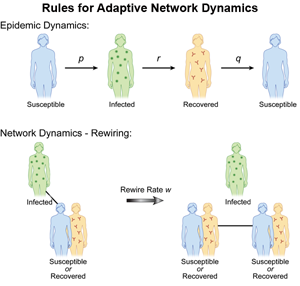
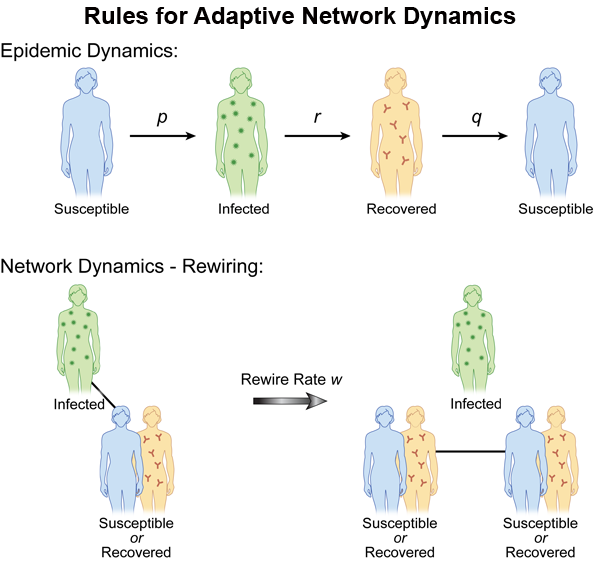
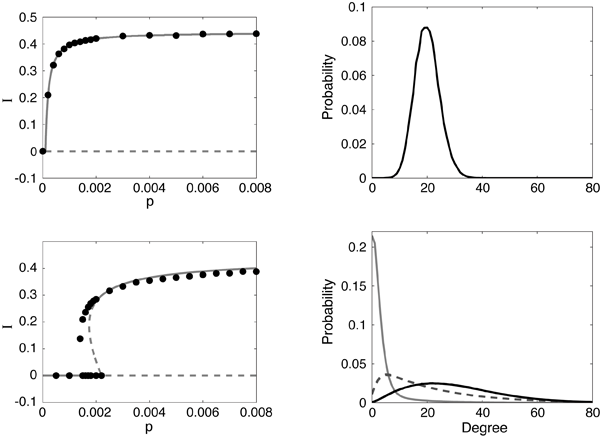
We do note that many of the agent-based and multiscale models take into account distributions of human motion, thereby causing contacts that are time dependent and heterogeneous. In contrast to the models of a static network or models with externally applied changes in structure, a new class of models based on endemic populations on an adaptive network has been recently introduced [30]. (For a recent review, see also Ref. [31].) Changes to the network structure are made in response to the epidemic spread and in turn affect future spreading of the epidemic. Here, the important new parameter is the rewiring rate of the network, which governs changes in the fraction of susceptible (S) to infective (I) links. The network alters dynamically when there are contacts between S and I, and social pressures (the desire to avoid illness) rewire the contacts, replacing them with noninfectious contacts (see Fig. 2). In this way, infections are reduced because infectives become isolated, and a new phenomenon occurs: for an appropriate choice of parameters, it is possible to observe a bistability between the disease-free equilibrium and an endemic state. In contrast, static networks in a large population typically predict either a single attracting endemic or disease-free state.

Illustration: Carin Cain

Illustration: Carin Cain

×

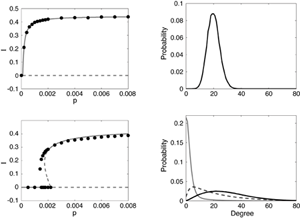
When modeling adaptive networks, one needs to describe the disease status of the individual as well as contact behavior for each individual. Both nodes (people) and links (contacts between people) must be modeled as functions of time. Suppose we have S, I, and R states available for each node. If a node in an infected state is linked to a susceptible node, the avoidance behavior says the S node should rewire by changing its link to a noninfectious node, such as an S or R node. Since the model is a finite population with random transitions between contacts and states, we assume there is a rewiring rate at which the new contacts are made probabilistically [32]. Comparing the model with adaptive social behavior to the fixed contact models, the results are quite dramatic. First, new attractors leading to bistability appear for small rewiring rates [30,32–34]. (In Refs. [33,34], SI links are removed and susceptibles reconnect to randomly selected nodes, independent of their infection status, but the results are qualitatively similar.) An example of the behavior is shown in Fig. 3. In addition, the size of the fluctuations increases, which may lead to higher probabilities of disease extinction [32].

×

A complication is the possibility that individuals may not have full knowledge of their own and others’ infection status. The presence of asymptomatic infectious individuals can occasionally lead to disease avoidance behavior being counterproductive [34]. Co-spreading of an epidemic and awareness of the epidemic has been considered, where the network structure was held fixed but the connection strength reduced for nodes that were aware of the need to protect themselves from the disease [35]. This behavioral response increased the epidemic threshold—the point at which one would say there is an epidemic—and was most effective when the awareness was transmitted on the same contact network as the infection.

Almost all diseases exhibit a certain amount of randomness in how they spread, which results in fluctuations in the number of disease cases—say, a time series of disease cases exhibiting complex, possibly uncorrelated, local increases in the number of infectives. As diseases evolve in large populations, there is the possibility that they will become extinct in a finite time. Extinction occurs when the number of infectives becomes so small that there is insufficient transmission to keep the disease in its endemic state. On the other hand, fade-outs are defined as temporary local extinction, where infections reappear through reintroduction of the disease. Fluctuations cause the fade-out or extinct state to be reached in a finite time. Populations based upon adaptive networks further complicate the problem, since social dynamical situations, such as disease avoidance strategies, can cause both the endemic and extinct states to be bistable [30,32].

A major characteristic of fluctuation-induced extinction in globally connected, stochastic models for large populations is the extinction rate. Viewing disease fade-out as coming from a system far from thermal equilibrium, finite population extinction rate laws have been derived in SIS [36,37] and SIR [38] models. Recently, non-Gaussian random vaccination (explained in greater detail below) has been used to derive enhanced extinction rates in such stochastic models [7].

Vaccine strategies have also been considered for epidemics that spread along networks where the contacts are static. Targeting high-degree nodes has been shown to be more effective than random vaccination for scale free networks [39,40], small world networks [41], and other social network geometries [42]. Since targeting the highest degree nodes requires full knowledge of the network geometry, related methods based on local knowledge have been developed, as in Ref. [43].

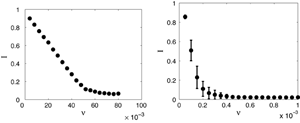
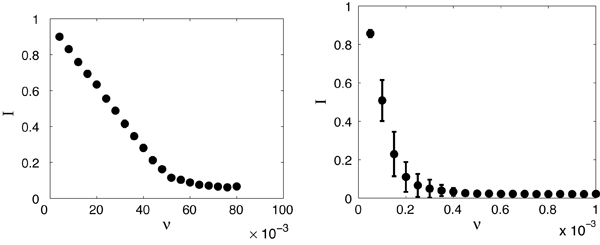
Recently, we used a random non-Gaussian vaccination strategy and found that in conjunction with adaptive rewiring, it is extremely effective. We assumed that pulsed vaccination was a Poisson process with fixed amplitude (fraction of susceptibles vaccinated) and a mean frequency $\nu$ of application to the population. Figure 4 compares the effectiveness of a vaccine in a model with (right) and without (left) network adaptivity. (See Ref. [44] for details.) To eliminate disease, vaccination should target susceptibles in the population. Because of the adaptivity of the network, rewiring leads to susceptibles with a higher degree on average. Random vaccination of the susceptible population will automatically tend to target higher degree nodes and is therefore expected to be much more effective than when applied to a static network, where the high degree nodes are likely to be infectious and not selected for vaccination.

×

In the presence of a disease—especially those that are highly publicized—individuals and societies will adapt their behavior. For example, during the 2002–2003 SARS outbreak in China, people began washing their hands more often and wearing masks [45] and those who were sick sought out health services more frequently [46]. In the language of networks, these can be considered behaviors that, respectively, reduce the effective strength of links between individuals and change the contact network itself.

New models of epidemics that make use of the adaptive behavior of the population will be able to make better predictions of when an outbreak will occur. Preliminary analysis of the effect of vaccine controls that work synergistically with the rewiring of the contact structure may indeed lead to better strategies for eradicating diseases. This may be especially true in the presence of limited resources. We expect that combining adaptive networks with other more complex population models will help us better predict and avoid epidemics. Moreover, we expect that understanding adaptive responses to a disease in a population will lead to new research directions and contributions to the field of behavioral epidemiology.

We gratefully acknowledge support from the Office of Naval Research, the Army Research Office, and the Air Force Office of Scientific Research. L.B.S is supported by Award Number $\text{R}01\text{GM}090204$ from the National Institute Of General Medical Sciences. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute Of General Medical Sciences or the National Institutes of Health.