Race for Majorana fermions

Marcel Franz

Viewpoint

Race for Majorana fermions

Department of Physics and Astronomy, University of British Columbia, Vancouver, BC, Canada V6T 1Z1

March 15, 2010• Physics 3, 24

The race for realizing Majorana fermions—elusive particles that act as their own antiparticles—heats up, but we still await ideal materials to work with.

Figure caption — **Figure 1:** Various electron dispersions that can lead to a topologically nontrivial superconducting state with Majorana fermion excitations. Red bands represent occupied single-electron states and the arrows indicate the orientation of electron spins. (a) Parabolic dispersion characteristic of a 2D electron gas with negligible spin-orbit coupling. For each momentum $k$ there are two degenerate spin projections. In this case, electrons must be paired with an unconventional spin-triplet $p_{x} + i p_{y}$ order parameter to produce a topological superconductor [6]. (b) Helical liquid on the surface of a topological insulator characterized by Dirac energy dispersion. There is one spin state at each momentum $k$ with orientation perpendicular to $k$ . An ordinary $s$ -wave pairing leads to topological superconductivity [7]. (c) 2D electron gas with strong spin-orbit coupling in the presence of ferromagnetic insulator or in-plane magnetic field discussed in Refs. [3, 8]. The upward canting of spins signifies broken time-reversal invariance. In this case, an $s$ -wave pair potential induced by the proximity effect generates a topological superconductor characterized by a mixture of the spin-singlet $s$ -wave and spin-triplet $p$ -wave order parameters.

In quantum theory, spin-1/2 particles, like electrons, are described by complex-valued solutions of the celebrated Dirac equation. In a seminal 1937 paper Ettore Majorana [1], guided by principles of simplicity and mathematical elegance, proposed a modification to the Dirac equation describing a spin- $1 / 2$ particle that would admit purely real (as opposed to complex-valued) solutions. Such real solutions have become known as Majorana fermions and describe a class of particles that are, curiously, their own antiparticles (more on this below). There are compelling theoretical reasons to believe that neutrinos are Majorana fermions but a convincing experimental proof is yet to be given [2]. Over the past decade Majorana fermions have been increasingly studied in condensed matter physics where they can appear as emergent degrees of freedom in certain systems of interacting electrons. This means that at low energies the system behaves as if composed of Majorana fermions and not the constituent electrons. In this context, the interest in Majorana fermions stems from their exotic properties (such as the non-Abelian exchange statistics) that could find uses in future applications to fault-tolerant quantum information processing. Jason Alicea of the California Institute of Technology, US, in a paper in Physical Review B [3], describes the most recent and by some measures perhaps the most promising of the proposals to realize and control Majorana fermions in a solid-state system.

Majorana fermions are more easily understood in the “second quantized” notation. Ordinary fermions, such as electrons or protons, are described by creation and annihilation operators: $c_{j}^{†}$ creates a fermion in a quantum state $j$ while $c_{j}$ annihilates it (or, equivalently, creates the corresponding antiparticle). Their Fermi-Dirac statistics is encoded in the canonical commutation relations ${c_{i}^{†}, c_{j}^{†}} = {c_{i}, c_{j}} = 0$ and ${c_{i}^{†}, c_{i}} = 1$ , where curly brackets denote anticommutator. The key property of ordinary fermions is that, evidently, $c_{i}^{†} \neq c_{i}$ , i.e., particles and antiparticles are physically distinct.

Now imagine that for some reason it becomes more natural to describe the system at hand not in terms of the fundamental constituent fermions $c_{j}$ but instead in terms of new emergent particles related to them as $γ_{j 1} = (c_{j}^{†} + c_{j}) / 2$ and $γ_{j 2} = (c_{j}^{†} - c_{j}) / 2 i$ . These $γ$ -particles obey the same fermonic commutation relations but, crucially, it now holds that $γ_{j α}^{†} = γ_{j α}$ , i.e., the particle acts as its own antiparticle! Thus $γ_{j α}^{†}$ is a creation operator of a Majorana fermion. Formally, it is always possible to cast the theory of an arbitrary system containing, say, electrons, in terms of Majorana fermions using the above transformation. In the vast majority of cases such a manipulation does not provide any benefit. There are systems, however, in which such a description—and no other—is required to capture the underlying physics.

If neutrinos are Majorana particles then, clearly, the construction outlined above applies to them. In condensed matter physics, Majorana fermions appear as elementary excitations in theories describing certain fractional quantum Hall states [4], interacting quantum spins [5], and exotic superconductors [6]. The proposal by Alicea [3] builds upon and improves some of the recent proposals [7,8] for realization of Majorana fermions in superconductors.

How do superconductors give rise to Majorana fermions? Those familiar with the Bardeen-Cooper-Schrieffer (BCS) theory of superconductivity will recognize that combinations of electron creation and annihilation operators similar to those that define $γ$ particles also enter the microscopic description of superconductors. Physically, such mixing of the particle and hole degrees of freedom underlies the pairing phenomenon fundamental to the BCS theory. Thus it is perhaps not surprising that Majoranas emerge in this context. However, it takes a very special superconductor to realize a “useful” Majorana fermion that can be viewed as a legitimate excitation, localized in space and well separated from all other such excitations. To see how this comes about, recall that a necessary step in the BCS theory is doubling of the degrees of freedom whereby one considers two copies of the underlying metal, one in terms of electrons and one in terms of holes. When the pairing interaction is switched on, the spectrum of the BCS Hamiltonian retains two branches, one with positive energies and one with negative, related by the particle-hole transformation. In the final counting, only half of the states are physical: one takes, for example, the positive energy branch while the other one must be discarded. There are situations, however, where a single unpaired state appears exactly at zero energy [9]. When this happens, the above discussion implies that only a half of that state is in fact physical. It turns out that this “half-state” has properties of the Majorana fermion.

In ordinary superconductors, such as lead or aluminum, which are characterized by an order parameter with $s$ -wave symmetry, such zero-modes do not occur. They do occur in the vortex core of “topological” superconductors such as the so-called spin-triplet $p_{x} + i p_{y}$ superconductor [6]. Unfortunately, there are at present no known materials with this property. ${Sr}_{2} {RuO}_{4}$ is widely believed to have a spin-triplet order parameter but its detailed structure is controversial and probably not of the kind needed to realize the unpaired Majorana fermions. Although a suitable material may yet be discovered, it would appear that nature does not favor the exotic superconducting order necessary to produce Majoranas.

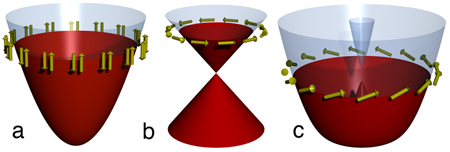
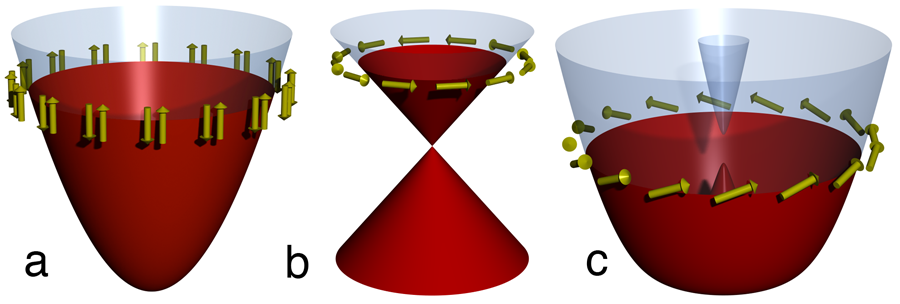
An ingenious proposal to artificially engineer a topological superconductor has been advanced by Fu and Kane [7] based on the exotic properties of the electronic states on the surface of a topological insulator [10]. They envision inducing superconducting order at the surface through the proximity effect by coating it with a superconducting film. The latter can be of ordinary $s$ -wave variety but the superconducting state induced in the interface will still be topologically nontrivial owing to the unusual form of the surface electron kinetic energy inherited from the topological insulator, illustrated in Fig. 1 (b). The mathematical description of the surface superconducting state created in this way is nearly identical to the theory of the spin-polarized $p_{x} + i p_{y}$ superconductor mentioned above. A vortex in this superconductor will carry an unpaired Majorana fermion.

Although the ingredients necessary to realize the Fu-Kane proposal in a laboratory are, in principle, available, in practice, significant experimental hurdles exist. Perhaps the most formidable of these is the fact that all of the known topological insulators ( $BiAs$ alloys and ${Bi}_{2} {Te}_{3}$ , ${Bi}_{2} {Se}_{3}$ crystals) are not very good bulk insulators. As a result, the all-important surface states overlap in energy with the bulk electronic states and this will affect the fragile Majoranas in unpredictable ways.

Sau and co-workers [8] recently noted that conditions similar to those envisioned by Fu and Kane can be achieved using more conventional ingredients. All one needs is a semiconductor quantum well coupled to a ferromagnetic insulator on one side and an ordinary superconductor on the other. If the electrons in the quantum well experience sufficiently strong spin-orbit coupling, such as those in $InAs$ , then they will behave in a way that is sufficiently similar to the surface electrons in a topological insulator [see Fig. 1 (c)] and can form a topological superconductor with just the right properties to harbor the Majorana fermions.

A possible weak point of the above proposal is the need for a ferromagnetic insulator, which is fairly rare in nature (most ferromagnets are metallic). A key insight of Alicea’s work [3] is a way to circumvent this problem. He shows that for a certain form of the spin-orbit coupling (characterized by the right mixture of the so-called Rashba and Dresselhaus terms), the effect of the ferromagnetic insulator can be substituted by an external magnetic field applied in the plane of the interface. The required spin-orbit coupling occurs, e.g., in zincblende quantum wells grown in the (110) crystal direction. In a semiconductor with a large $g$ -factor, such as $InSb$ , only moderate magnetic field strength of order $1$ Tesla is required to drive the transition into the topological superconducting state. An additional benefit of this scheme is the ability to tune between ordinary and topological superconductors by adjusting the magnetic field strength.

Recent theoretical proposals to engineer two-dimensional quantum phases of electronic matter that behave as topological superconductors [3,7,8] give hope that the elusive Majorana particles, predicted more than 70 years ago, will soon be realized in a tabletop experiment. Which of the proposed schemes will ultimately lead to a useful device is difficult to predict. Proposals by Sau et al. [8] and by Alicea [3] build upon recent theoretical advances but use rather conventional ingredients whose physics and technological aspects are well understood, which might give them an edge in the race for the first experimental realization. The Fu-Kane proposal [7] is conceptually simpler and more elegant, but the technology based on topological insulators, which constitute the key ingredient here, is still in its infancy. On the other hand, discoveries of new families of topological insulators are reported on a regular basis [10,11] and it appears that it is only a matter of time for an ideal material to emerge. In any case, it is clear that the race for Majoranas is now in its final stretch.

References

E. Majorana, Nuovo Cimento 5, 171 (1937)
F. Wilczek, Nature Phys. 5, 614 (2009)
J. Alicea, Phys. Rev. B 81, 125318 (2010)
G. Moore and N. Read, Nucl. Phys. B 360, 362 (1991)
A. Kitaev, Ann. Phys. 303, 2 (2003)
N. Read and D. Green, Phys. Rev. B 61, 10267 (2000)
L. Fu and C. L. Kane, Phys. Rev. Lett. 100, 096407 (2008)
J. D. Sau, R. M. Lutchyn, S. Tewari, and S. Das Sarma, Phys. Rev. Lett. 104, 040502 (2010)
R. Jackiw and P. Rossi, Nucl. Phys B 190, 681 (1981)
M. Z. Hasan and C. L. Kane, arXiv:1002.3895
M. Dzero et al., Phys. Rev. Lett. (to be published); arXiv:0912.3750; H. Lin et al., arXiv:1003.0155; B. Yan et al., arXiv:1003.0074; S. Chadov et al., arXiv:1003.0193

About the Author

Marcel Franz studied physics as an undergraduate at the Comenius University in Bratislava, Czechoslovakia, and received his Ph.D. from the University of Rochester in 1994. After postdoctoral appointments at McMaster and Johns Hopkins Universities, he was appointed Assistant Professor (2000), and later Associate Professor (2006) at the University of British Columbia. He received the A. P. Sloan Fellowship (2004), and become a member of the Canadian Institute for Advanced Research (2003). His main research interests include superconductivity, strongly correlated electron systems, and all things unusual. He also likes to spend time at the Aspen Center for Physics and the Kavli Institute for Theoretical Physics (KITP) in Santa Barbara.