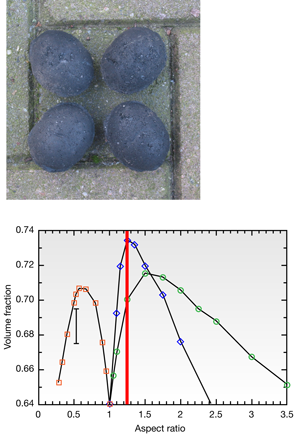
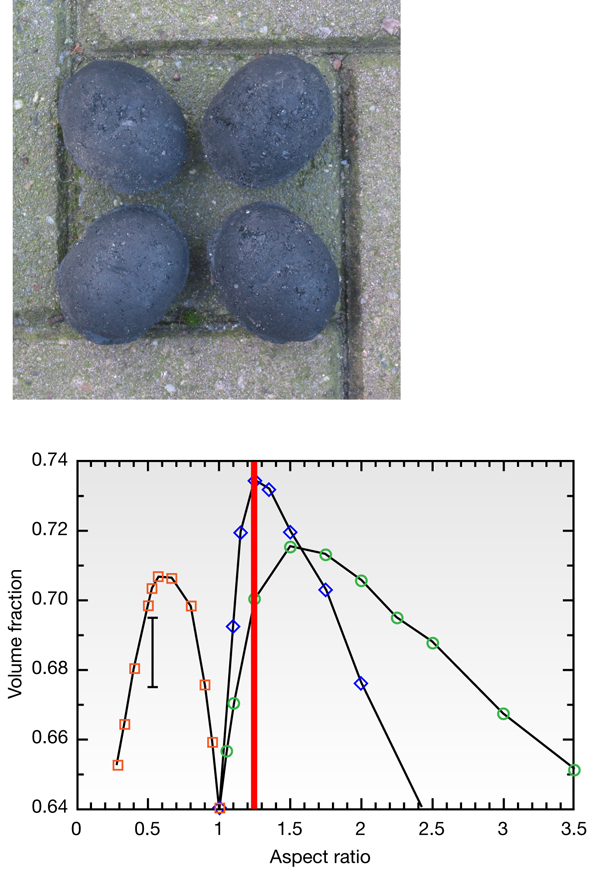
The tetrahedral dice are cast … and pack densely

Daan Frenkel

Viewpoint

The tetrahedral dice are cast … and pack densely

Department of Chemistry, University of Cambridge, Cambridge CB2 1EW, UK

May 3, 2010• Physics 3, 37

Magnetic resonance images of tetrahedral dice show a density of random close packing, in agreement with recent calculations.

Figure caption — **Figure 1:** Tetrahedral objects have been found to pack with high density, even denser than other non-spherical objects that have been designed to pack densely. “Egg cokes” produced from compressed coal powder (top) have a roughly biaxial, ellipsoidal shape. The aspect ratio of these coal briquettes coincides remarkably closely with that of biaxial ellipsoids that, according to the study of Donev *et al.* [11] have the highest density of RCP of all possible biaxial ellipsoids (red line in bottom panel).

Tetrahedra are special among the platonic solids. They are the simplest polyhedra and the ones most unlike spheres. Surprisingly, much of our knowledge about the packing properties of tetrahedra is very recent: the past year has witnessed a sudden proliferation of novel, and often surprising, findings. Using Monte Carlo simulations, Haji-Akbari et al. [1] found that, upon compression, systems of hard tetrahedra spontaneously form a very dense quasicrystalline structure. Now, in a paper in Physical Review Letters, Alexander Jaoshvili, Massimo Porrati, and Paul Chaikin of New York University and Andria Esakia at Virginia Polytechnic Institute, both in the US, report their experiments on (almost) tetrahedral dice, which shed new light on the disordered structures that result when tetrahedra particles are poured into a (large) container [2].

Before discussing tetrahedral packing, it is useful to consider first the venerable (yet still not fully solved) problem of sphere packing. In 1611 Kepler proposed that the densest packing of spheres could be achieved by stacking close-packed planes of spheres. In such a packing, the spheres occupy $π / \sqrt{1} 8 \approx 74.05 %$ of space. The Kepler conjecture was (almost certainly) proven in 1998 by Thomas Hales. However, that does not mean that we know all there is to know about sphere packings: in addition to regular packing, spheres (and, in fact, most hard particles) also exhibit a much less understood packing, namely, random close packing (RCP).

The quantitative study of random close packing started with J. D. Bernal’s experiments on the packing of ball bearings [3]. His experiments (and those of many others) suggested that it is impossible to compress disordered sphere packings beyond a volume fraction of approximately $64 %$ . However, this observation does not necessarily imply that there exists a well-defined density of random close packing. It could just as well be that the rate at which the disordered hard-sphere packings can be compacted becomes very small around a volume fraction $64 %$ —small, but not zero. If that were the case, RCP would not have a clear mechanical definition (that is, pouring and shaking may not lead to a well-defined RCP state). Indeed, in 2000, Torquato, Truskett, and Debenedetti [4] argued on the basis of computer simulations that states with a density above $64 %$ can always be obtained by increasing the local order in a “random” sphere packing. This observation implies that the “mechanical” route to random close packing may be ill defined.

A different, “nonmechanical” way to view random close packing was proposed a few years ago by O’Hern et al. [5,6]. The basic idea of their approach is the following: start with a random configuration of $N$ particles in a volume $V$ , interacting through a soft repulsion with a finite range $σ$ ( $σ$ is equal to the diameter of the hard spheres that I consider later). For every random configuration, we can now determine the nearest minimum or zero of the potential energy. At low densities, the states with zero potential energy will occupy a finite fraction of configuration space. However, as we decrease the volume of the system, the nearest local energy minima (the “inherent structures,” to use the language of Stillinger and Weber [7]) will one-by-one take on a finite value of the potential energy. For every set of (scaled) coordinates, there is a unique density where this first happens. If we consider the limit that the soft particles become hard spheres, then this density is the point where this specific inherent structure is no longer allowed.

The key observation by O’Hern et al. [5] is that the simulations show that the rate at which allowed inherent structures disappear with increasing density, has a sharp maximum at a particular density. Moreover, this peak becomes sharper as the system size becomes larger. In the thermodynamic limit, the number of allowed inherent structures therefore appears to decrease discontinuously at a hard-sphere volume fraction that happens to be very close to existing estimates of the density of random close packing. The fact that a sharp transition appears to exist implies that the evaluation of the density of RCP is now a mathematical problem—RCP is a property of three-dimensional space. But, and this is quite unusual, unlike regular close packing that can be exhibited by periodically repeating a Wigner-Seitz cell containing only a single particle, RCP is “emergent,” it is NOT a property of a small system and becomes only meaningful in the thermodynamic limit.

In the case of tetrahedra, the density of regular close packing is not known, nor is the density of random close packing. In fact, until two years ago, it was not even known if tetrahedra could pack more densely than spheres [8]. Earlier, Ulam had made the conjecture that, of all hard convex bodies, spheres occupy the smallest volume fraction at regular close packing (however, Ulam apparently never wrote down his conjecture—it is quoted in a book by Martin Gardner [9]). But until the work of Chen [8], there existed no example of a packing of tetrahedra denser than that of spheres. During the past year, it has become clear that not only do tetrahedra pack more densely than spheres, but also much more densely. In particular, Haji-Akbari et al. [1] used numerical simulations to study the high-density packing of hard tetrahedra and observed a packing fraction of more than $85 %$ —and since then, even higher packing densities have been reported by several authors [10].

But, and this is really unexpected, some of the highest density packings found by Haji-Akbari et al. [1] are not crystalline, but quasicrystalline (a dodecagonal quasicrystal). It is still possible that the densest packing of tetrahedra is crystalline (but then the crystal structure is nontrivial), yet the fact that hard tetrahedra spontaneously form a quasicrystal upon compression was totally unexpected.

Haji-Akbari et al. also found that the density of random close packing of tetrahedra is very high (above $78 %$ , which is also above the Kepler limit). For particles that are not space-filling, this result is also surprising. As in the case of spheres, one can argue about the precise meaning of random close packing.

The experimental ”Bernal” approach to random close packing of tetrahedra was followed in this new set of experiments by Jaoshvili et al. [2] who poured tetrahedral dice into various containers and used volumetric measurements to determine the density of RCP and MRI to analyze the local structure of the resulting packing. These experiments suggest a density of random close packing around $76 \pm 2 %$ , roughly in agreement with the findings of Haji-Akbari et al. [1]. Interestingly, Jaoshvili et al. find that positional and orientational correlations of randomly packed tetrahedra are very short ranged, suggesting that there is no precursor of the quasicrystalline state in the dense fluid.

The experiments on packing of tetrahedra raise an interesting question about the “technology” of random close packing. There are many practical examples where man-made objects are designed such that they will efficiently fill the volume into which they are poured. Examples are many pills (both oblate and prolate), candies (such as the M&Ms studied in 2003 by Donev et al. [11]) or, on a larger scale, egg-shaped coal briquettes. In particular in the latter case, there is a clear incentive to design the shape of the object such that the density of random close packing is maximal, because briquettes are used as fuel and the higher their RCP density, the smaller the storage requirements. Interestingly, ”egg cokes” have the shape of a biaxial ellipsoid with an aspect ratio that corresponds closely to the shape that Donev et al. found to have the highest density of random close packing of any ellipsoid (approximately $73.5 %$ , see Fig.1). This suggests that the coal engineers of the 19th century had a good understanding of the effect of shape on random close packing—except that they did not make tetrahedral briquettes! Yet such objects would pack more densely than biaxial ellipsoids. Almost certainly, the nonexistence of the tetrahedral briquette is not due to an oversight of the coal engineers: most likely tetrahedral objects would chip and fracture much more easily than ellipsoids.

References

A. Haji-Akbari et al., Nature 462, 773 (2009)
A. Jaoshvili, A. Esakia, M. Porrati, and P. M. Chaikin, Phys. Rev. Lett. 104, 185501 (2010)
J. D. Bernal, Nature 185, 68 (1960)
S. Torquato, T. M. Truskett, and P. G. Debenedetti, Phys. Rev. Lett. 84, 2064 (2000)
C. S. O’Hern, L. E. Silbert, A. J. Liu, and S. R. Nagel, Phys. Rev. E 68, 011306 (2003)
L. E. Silbert, A. J. Liu, and S. R. Nagel, Phys. Rev. E 73, 041304 (2006)
F. H. Stillinger and T. A. Weber Science 225, 983 (1984); Phys. Rev. A 28, 2408 (1983)
E. R. Chen, Discrete Comput. Geom. 40, 214 (2008)
The Ulam conjecture is mentioned in: M. Gardner, The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems ( Norton, New York, 2001)[Amazon][WorldCat]
Y. Kallus, V. Elser, and S. Gravel, arXiv:0910.5226v5; S. Torquato and Y. Jiao, Phys. Rev. E (to be published); E. R. Chen, M. Engel, and S. C. Glotzer, arXiv:1001.0586
A. Donev et al., Science 303, 990 (2004)
http://de.wikipedia.org/wiki/Eierkohle

About the Author

Daan Frenkel is Professor of Theoretical Chemistry at the University of Cambridge, UK. His research focuses on numerical simulations of many-body systems, with a special emphasis on problems relating to ordering and self-assembly. He received his training at the University of Amsterdam and, subsequently worked at UCLA, Shell Research, Utrecht University, the FOM Institute for Atomic and Molecular Physics, and the University of Amsterdam.