Cool quarks

Mark Alford

Viewpoint

Cool quarks

Mark Alford

Department of Physics, Washington University in St. Louis, St. Louis, MO 63130, USA

May 24, 2010• Physics 3, 44

New calculation of quark matter properties tells us what an exotic quark-neutron star might look like.

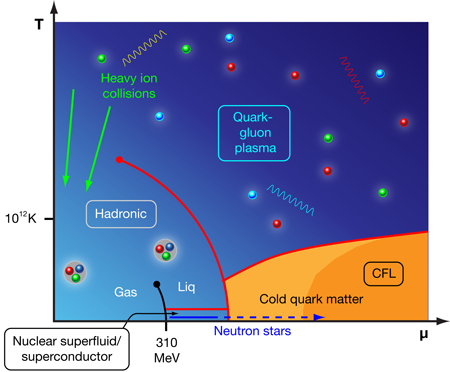
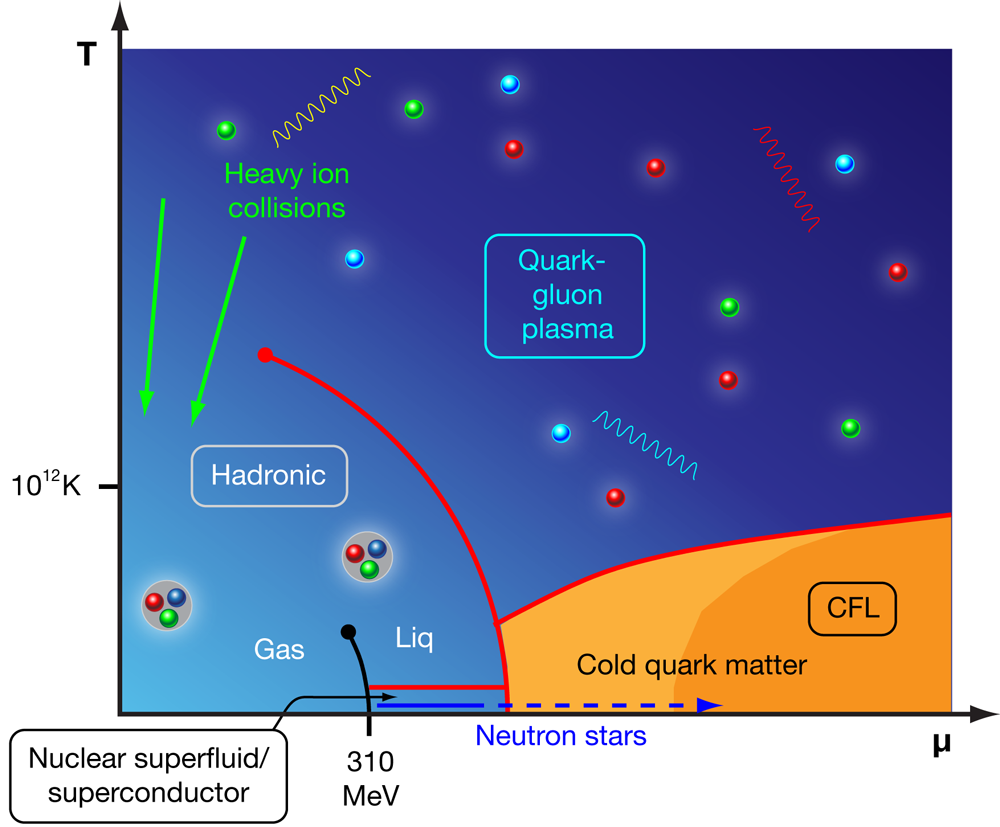
Figure caption — **Figure 1:** Schematic phase diagram of matter at extreme density and temperature. The vertical axis represents temperature. The horizontal axis is the quark chemical potential $μ$ . As $μ$ increases at low temperature, the system passes from vacuum to nuclear matter at $μ \approx 310 MeV$ . At an unknown higher chemical potential there is a transition to quark matter, which, at sufficiently high density, is expected to be in the color-flavor-locked (CFL) phase. Neutron star matter is in the lower part of the phase diagram, ranging up to an unknown maximum density at the center of the star.

Mapping the phases (Fig. 1) and properties of matter under extreme conditions—such as the highest achievable pressures and densities—is a major ongoing project in nuclear and particle physics [1]. At ultrahigh pressures (where the baryon density is significantly higher than the nuclear density), but at temperatures that are not too high ( $T \leq 100 MeV$ ), researchers expect a rich phase diagram with exotic forms of matter, including quark matter where quarks are no longer bound into separate baryons [2]. However, investigating matter in this regime presents substantial experimental and theoretical challenges.

The only place in nature where we find equilibrated matter above nuclear density is inside a neutron star—not a convenient laboratory. Information about the interior of an object like this is inferred from astronomical observations of its behavior. Such observations, however, are difficult to use to confirm or refute hypotheses about the phases of dense matter because firm theoretical predictions are also problematic. The strong interaction plays a major role in the physics of high-density matter, and although we have a well-confirmed theory—quantum chromodynamics (QCD)—there are few reliable calculational techniques for handling it. The only known first-principles approaches are perturbation theory, which is valid at sufficiently high density where the QCD coupling $α_{s}$ becomes small, and brute-force numerical computation using lattice gauge theory, which is currently blocked by the fermion sign problem from giving any predictions about the high-density low-temperature regime [3].

A paper appearing in Physical Review D [4] by Aleksi Kurkela at the ETH in Switzerland, Paul Romatschke at the University of Washington, Seattle, in the US, and Aleksi Vuorinen at the University of Bielefeld in Germany represents significant progress in our understanding of a typical form of quark matter that is conjectured to occur in neutron stars, namely quark matter involving the three lightest quark flavors (up, down, and strange), without any Cooper pairing of the quarks. Kurkela et al.’s calculation of the equation of state (EOS) of such matter is the first one to include strong interaction effects to order $α_{s}^{2}$ and the effects of the strange quark mass. This is an important result for three reasons. First, we are beginning to have real observational constraints on the EOS because it determines the mass-radius relation $M (R)$ for neutron stars. Second, the strange quark mass is expected to play a very important role in the properties of quark matter [2]. Third, the authors’ approach is rigorously correct in the limit of asymptotically high density, and is systematically improvable by going to higher order in $α_{s}$ . This is in contrast to other commonly used approaches such as Nambu-Jona-Lasinio (NJL) models [5,6], which include some relevant physics but have no clear relationship to the correct QCD calculation.

Kurkela et al. used their EOS to predict $M (R)$ for neutron stars. Their most robust conclusion relates to the maximum mass that any neutron star can have—beyond that mass the star collapses to a black hole. Many previous calculations (see, for example, Ref. [7]) using NJL and other models had predicted a highly compressible “soft” EOS for quark matter and consequently a low maximum mass, of order $1.6 M_{⊙}$ , for neutron stars with a quark matter core (“hybrid” stars). This led to a widespread expectation that finding a star heavier than about $1.6 M_{⊙}$ would rule out the presence of quark matter in the star’s interior, indicating that all neutron stars up to that mass are purely nucleonic with no quark matter core, and that quark matter only occurs at very high densities. However, Kurkela et al.’s quark matter EOS is not soft, and they found that hybrid stars can have masses up to nearly $2 M_{⊙}$ . This result agrees with earlier work [8], which used a phenomenological parameterization of the quark matter EOS [9] based on earlier perturbative calculations [10]. The emerging conclusion [11] is that if observers find a neutron star with a mass as high as $2 M_{⊙}$ , that star could have a quark matter core, and a transition to quark matter at moderate density (e.g., twice nuclear density) will not be ruled out. As it becomes possible to measure the radius as well as the mass of neutron stars we may learn more about the EOS of dense matter (see, for example, Ref. [12], which suggests $R$ ≲ $10 km$ and $M \sim 1.7 M_{⊙}$ , which is hard to explain with any purely nucleonic equation of state). The presence of quark matter in neutron stars may also be experimentally tested by using observables such as cooling rate and spin down, which are influenced by transport properties of quark matter [2].

Kurkela et al.’s calculation does not eliminate uncertainty about the EOS of quark matter at the densities relevant to neutron stars. First, as Kurkela et al. themselves note, there are very general reasons for expecting that the ground state of three-flavor quark matter at sufficiently high density will be not “normal,” but Cooper-paired, in the color-flavor-locked (CFL) phase [13], where green up quarks pair with red down quarks, red strange quarks with blue up quarks, etc (see Ref. [2] for further explanation). Second, Kurkela et al.’s calculation is rigorously valid only at asymptotically high densities, where the QCD coupling is sufficiently small. Their own tests indicate that their results become reliable at the $10 %$ level when the quark chemical potential is above $1 GeV$ . This corresponds to matter a hundred times denser than nuclear matter—far beyond the values that we think can be sustained in the core of a neutron star.

For both these sources of uncertainty, Kurkela et al. estimated likely sensitivity of their results to the relevant unknown parameters. They introduced into their EOS a term that estimates the maximum effect of color-flavor locking, parameterized by the unknown CFL gap parameter $Δ$ (expected to be ≲ $100 MeV$ ). They also studied the effects of varying the renormalization scale $\bar{Λ}$ in their perturbative calculation. This does not include nonperturbative physics such as confinement, but is a rough guide to the reliability of their calculation. Their key finding of high maximum masses was insensitive to variation in these parameters.

In addition to astrophysical observables, Kurkela et al. also investigated the “strange matter hypothesis”— that three-flavor quark matter is more stable than nuclear matter, even at zero pressure—by surveying the parameter space of their theory to see when the strange matter hypothesis was correct. In this case the CFL pairing gap played a significant role: without CFL pairing, there was a much smaller region of parameter space where quark matter is more stable than nuclear matter. This confirms previous calculations made with more phenomenological models [14].

If the strange matter hypothesis is false then there is a transition from nuclear matter to quark matter at some critical density or range of densities. Kurkela et al. tested whether their perturbative EOS for quark matter can be matched to standard equations of state for nuclear matter, nuclear matter with a condensate of kaons, or nuclear matter that includes hyperons (strange baryons such as $Λ^{0}$ , $Σ^{-}$ , etc). They found that, imposing reasonable physical conditions such as causality of sound waves and monotonicity of the energy density, the transition from kaon-condensed or hyperonic matter to quark matter occurred at quite moderate densities, one to two times nuclear density. For pure nuclear matter the transition occurred at a higher density, around four times nuclear density. This supports the idea that quark matter could well exist in nature, in the cores of neutron stars.

Kurkela et al. have greatly expanded the range of densities over which we can calculate the EOS for quark matter, and have provided the limiting behavior that any physically reasonable quark matter EOS should approach at high density. Their work should be taken into account by anyone developing phenomenological treatments of the quark matter EOS. Kurkela et al.’s paper also points the way to further work on the perturbative approach, such as applying it to the CFL phase, and to electrically charged forms of quark matter that may appear in mixed phases in neutron stars. As these theoretical advances are combined with better observational data on neutron stars, we will gain much greater understanding of the phases and properties of ultradense matter.

References

NSAC Long-Range Plan 2007, http://www.nscl.msu.edu/future/lrp2007.
M. G. Alford, A. Schmitt, K. Rajagopal, and T. Schafer, Rev. Mod. Phys. 80, 1455 (2008); arXiv:0709.4635
“The fermion sign problem” is the problem of evaluating the highly oscillatory integral that occurs when lattice field theory is applied to a system with a high density of fermions. See, for example, S. Hands, Prog. Theor. Phys. Suppl. 168, 253 (2007); arXiv:hep-lat/0703017
A. Kurkela, P. Romatschke, and A. Vuorinen, Phys. Rev. D 81, 105021 (2010)
S. P. Klevansky, Rev. Mod. Phys. 64, 649 (1992)
T. Hatsuda and T. Kunihiro, Phys. Rep. 247, 221 (1994); arXiv:hep-ph/9401310
G. F. Burgio, M. Baldo, P. K. Sahu, A. B. Santra, and H. J. Schulze, Phys. Lett. B 526, 19 (2002); arXiv:astro-ph/0111440
M. Alford, M. Braby, M. W. Paris, and S. Reddy, Astrophys. J. 629, 969 (2005); arXiv:nucl-th/0411016
E. S. Fraga, R. D. Pisarski, and J. Schaffner-Bielich, Phys. Rev. D 63, 121702 (2001); arXiv:hep-ph/0101143
B. Freedman and L. D. McLerran, Phys. Rev. D 17, 1109 (1978)
M. Alford et al., Nature 445, E7 (2007); arXiv:astro-ph/0606524
F. Ozel, G. Baym, and T. Guver, arXiv:1002.3153
M. G. Alford, K. Rajagopal, and F. Wilczek, Nucl. Phys. B 537, 443 (1999); arXiv:hep-ph/9804403
G. Lugones and J. E. Horvath, Phys. Rev. D 66, 074017 (2002); arXiv:hep-ph/0211070

About the Author

Mark Alford is a professor of theoretical physics at Washington University in Saint Louis, US. He graduated from Oxford University in 1984 and obtained a Ph.D. from Harvard University in 1990. He has held research positions at the University of California, Santa Barbara, and at Cornell University, the Institute for Advanced Study in Princeton, and MIT, as well as a lectureship at Glasgow University.