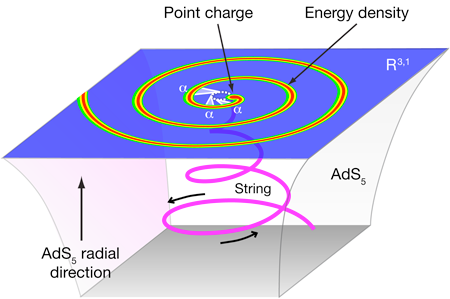
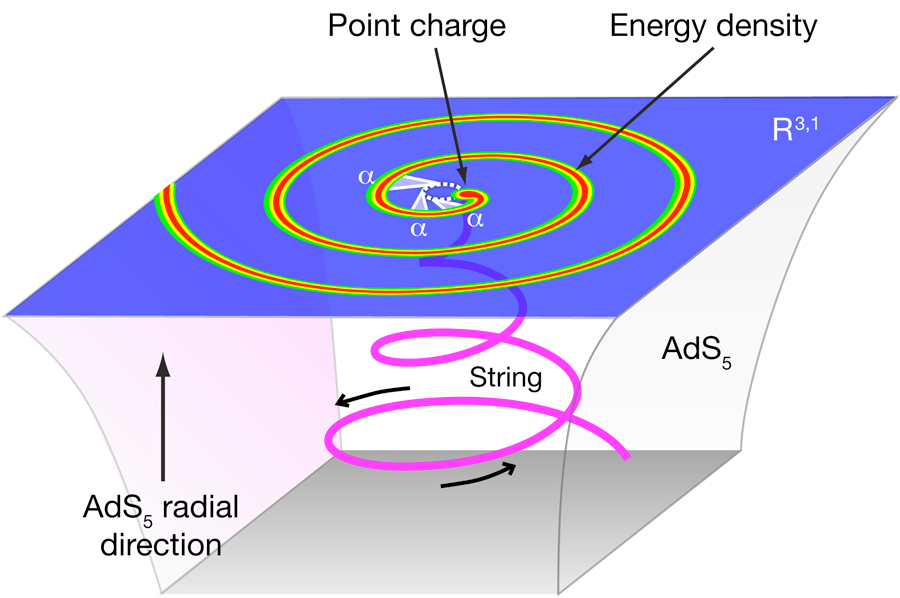
Synchrotron radiation from a single quark
Imagine a world in which , the dimensionless fine structure constant that characterizes the strength of the Coulomb interaction between two point charges, isn’t but in fact much larger than one. Further, imagine that in that world an energetic photon can break up into two lower energy photons, even in a vacuum. And imagine that the same large parameter that replaced governs the branching probability of the photon, so that it very rapidly breaks up into very many, very low energy photons. Now also imagine that in this world, one could build a synchrotron that guides a relativistic point charge around a circular trajectory at constant speed. What would the nature of synchrotron radiation be in this world? Would we find the same patterns as in our world—narrow cones of radiation pointing tangentially outwards from the circular trajectory? Or would the rapid branching of the photons lead to a perfectly round, uniform cloud of radiation completely washing out the information about the circular path the charge followed in the synchrotron? And why would anyone care to know?
It’s the first set of questions that has been answered in a paper by Christiana Athanasiou, Paul Chesler, Hong Liu, and Krishna Rajagopal from MIT and Dominik Nickel at the Institute of Nuclear Theory at the University of Washington in a paper recently published in Physical Review D [1]. Before discussing their findings, it is, however, worthwhile to address the last question. The method by which Athanasiou et al. attack the question about the synchrotron radiation is often referred to as holography. Some strongly interacting theories, like the one described above, can be completely solved by holography, a conjectured equivalence between the full quantum dynamics of a field theory and a classical gravitational problem in one higher dimension. In analogy with an optical hologram, all the information about the dynamics in the bulk gravitational theory is encoded in the field theory on the holographic screen, and vice versa.
Many such holographic pairs are now known, following Maldacena’s original proposal [2]. Some come with supersymmetry and some come without. The field theory part of the pair can have one, two, three, or more spatial dimensions. The field theory can be scale-free with a continuous spectrum of excitations, such as the one described in the introductory paragraph, or can have a discrete spectrum of bound states and a mass gap. What all these holographically solvable field theories have in common is a large number of degrees of freedom, for example, a large number of color degrees of freedom. Quarks can come in three different colors, but one can imagine similar theories in which this number is much larger than three. This large number allows for the dynamics to be captured by a classical theory. Holographically solvable field theories also require an intrinsic strong coupling parameter, such as the analog of above. While large, the class of solvable field theories so far does not, unfortunately, seem to include any theory that is actually known to be realized in nature.
Nevertheless, holography provides a set of solvable toy models of strong coupling dynamics. Such toy models are of use for physical problems where simply no calculational tools are available. In strongly coupled theories, perturbative techniques clearly are of little use. For real-time processes or in the presence of a finite density, computational techniques that rely on Monte-Carlo techniques—where configurations can be assigned a Boltzmann weighting factor and, correspondingly, only a small subset of all configurations has to be sampled—encounter serious challenges. One example of such a technique is our main nonperturbative tool for studies of the strong interactions: lattice gauge theory. So the qualitative insights gained from holographic models can be of great use when studying real-time dynamics of finite density systems in strongly interacting theories. The first example of such a qualitative insight is the result of Policastro et al. [3] and Kovtun et al. [4] that the shear viscosity-to-entropy ratio for a large class of holographic models is ), a value much smaller than in all calculable theories that were known or real world fluids that had been measured at that time. By now, theories are known with a ratio below ), also thanks to holography. But ) still remains the benchmark for strongly coupled fluids, not least because the quantum chromodynamic (QCD) plasma created at the Relativistic Heavy Ion Collider seems to require a value within a factor of . Motivated by this success, holography is used routinely to gain new intuition for various problems in high energy and, more recently, condensed matter physics.
But then why look at synchrotron radiation? After all, synchrotron radiation is textbook material and hardly needs an alternative explanation. Recall that only one property of the theory described in the first paragraph, a Coulombic force law between test charges, is reminiscent of electromagnetism. The second property, where the “photons” in the introductory paragraph can break up into pairs (branch, for short), is a property of gluons in QCD. A typical QCD-dominated event at a hadron collider, including the currently most powerful machines on earth, the Tevatron and the LHC, can be roughly split into three stages: an initial hard scattering event producing a few energetic partons (quarks and gluons); a subsequent showering stage in which each parton, via branching, broadens into a “jet” (a group of particles heading into roughly the same direction with total momentum and energy equal to that of the original parton); and a final hadronization stage in which the colored particles in the jet recombine into color-neutral mesons and baryons. Quantitative understanding of all three stages is required in order to be able to interpret Tevatron and LHC data. Both machines are dominated by QCD events. In order to disentangle new physics from rare QCD processes, rates for the latter need to be known with high accuracy.
Out of the three stages, showering is the one that most resembles the holographic toy model. But even without holography, a lot is known about showering using perturbative resummations, appropriate effective theories, as well as Monte Carlo models. Still, some puzzles remain, for example, about the angular energy distribution in the jet close to the trajectory of the original parton. Here, showering is dominated by the emission of many soft, almost collinear gluons. This situation is difficult for perturbative techniques, but very similar to the holographic toy models where all processes are dominated by very many, very soft partons.
If, in the holographic model, the strong branching washes out any jetlike structure and leads to completely spherical events, it would clearly be of little resemblance to real QCD. However, round and hence structureless events were precisely what Maldacena and Hofman [5] found for holographic quark/antiquark pairs produced by virtual photons. The question remained whether this is due to the way the virtual photon interacts with the “glue” (which in QCD is replaced by the perturbative hard scattering anyway) or whether it is due to showering. Hatta, Iancu, and Mueller [6] put forward a picture of parton branching that was able to explain several results in the holographic models and favors round jets as the result of showering. So the result of Athanasiou et al. came as somewhat of a surprise as they were able to establish that for synchrotron radiation the outgoing radiation in the holographic model forms the same sharp localized cones familiar from electromagnetism. Recall that this emitted radiation consists of this “glue”—force-carrying “photons,” which are neither real photons nor quarks and gluons. They are a lot like photons (which mediate a Coulomb interaction) and a little like gluons (they can split). Apparently, even in the strong coupling limit, showering does not wash out structures imparted on the initial emitted hard gluon. Comparisons to QCD are not doomed from the start. But whether the actual shape of the jets emitted by the synchrotron actually teaches us generic lessons that apply to QCD still remains to be seen.
Having laid out the context, we can finally discuss how Athanasiou et al. found their answer. A test charge in the field theory in the gravitational dual is represented by a string with its endpoint on the boundary of a five-dimensional spacetime, its tail hanging down. This setup is depicted in Fig. 1. The endpoint of the string represents the field theory charge; so for the problem of synchrotron radiation, one is looking for a string embedding subject to the boundary conditions that the string endpoint performs uniform circular motion. The force needed to keep the endpoint moving on this accelerated trajectory determines the total power of the emitted radiation, as was already found by Mikhailov [7]. The tail of the string is the holographic dual of the gluon cloud emitted by the string. In order to get the exact energy distribution in the field theory, one needs to solve the linearized gravitational deformation due to the string source. This still would be quite a formidable numerical problem, but what enabled Athanasiou et al. to come up with their simple answer was an analytic solution for the nonlinear string embedding, which made the subsequent linearized gravitational problem feasible.
While it still remains to be seen whether, in the end, this work will lead to a better understanding of the physics of jets at the LHC, it is clear that it has opened new doors and laid to rest some concerns about the usefulness of holographic models for jet physics. As a first step, one should now revisit proposals for realizing jets in a holographic theory, as have been put forward, e.g., in Ref. [8]. Holography allows one to study the detailed energy patterns in these jets, which apparently do not have to be round. To what extent it depends on initial conditions and whether it resembles the central region of a QCD jet remains to be seen.
References
- C. Athanasiou, P. M. Chesler, H. Liu, D. Nickel, and K. Rajagopal, Phys. Rev. D 81, 126001 (2010)
- J. M. Maldacena, Adv. Theor. Math. Phys. 2, 231 (1998); arXiv:hep-th/9711200
- G. Policastro, D. T. Son, and A. O. Starinets, JHEP 09, 043 (2002); arXiv:hep-th/0205052
- P. Kovtun, D. T. Son, and A. O. Starinets, Phys. Rev. Lett. 94, 111601 (2005); arXiv:hep-th/0405231
- D. M. Hofman and J. Maldacena, JHEP 05, 012 (2008); arXiv:0803.1467
- Y. Hatta, E. Iancu, and A. H. Mueller, JHEP 05, 037 (2008); arXiv:0803.2481
- A. Mikhailov, arXiv:hep-th/0305196
- P. M. Chesler, K. Jensen, and A. Karch, Phys. Rev. D 79, 025021 (2009); arXiv:0804.3110