Fermi gases as a test bed for strongly interacting systems

Daniel E. Sheehy

Viewpoint

Fermi gases as a test bed for strongly interacting systems

Daniel E. Sheehy

Department of Physics and Astronomy, Louisiana State University, Baton Rouge, LA 70803, USA

June 7, 2010• Physics 3, 48

A new perspective on strongly interacting fermions emerges from the experimental confirmation of a universal formula.

Figure caption — **Figure 1:** Schematic plot of the typical momentum distribution $n (k)$ of a fermion gas with short-range interactions, showing the characteristic behavior of $n (k)$ approaching a constant value below unity at $k \to 0$ and exhibiting a rapid variation near the Fermi wave vector $k_{F}$ (that would be a sharp discontinuity at $T \to 0$ for a Fermi liquid). At asymptotically large $k$ , as shown theoretically by Tan and confirmed experimentally by Stewart *et al.*, one has $n (k) \sim C / k^{4}$ (characterizing the fermions as they undergo collisions, seen in the inset), with the contact $C$ governing thermodynamic quantities like the total energy of the gas.

Some of the most vexing present-day problems in physics center on understanding the many-body properties and phases of strongly interacting fermions. Part of the difficulty arises from the fact that while the behavior of interacting fermions is understood in certain well-defined regions of parameter space, this understanding often breaks down in the correlated strongly interacting regime. Achieving this understanding of strongly interacting fermions would have wide-ranging implications: the systems of interest include high-temperature superconductors, high-density quark matter, and ultracold atomic fermion gases. The latter is the subject of a recent experimental investigation by John Stewart, John Gaebler, Tara Drake, and Debbie Jin at JILA in the US, appearing in Physical Review Letters [1]. Stewart et al. succeeded in confirming the validity of certain nonperturbative theoretical formulas, known as the Tan relations [2], which describe the properties of fermions with short-range interactions. The verification of these relations shows that cold-fermion experiments are particularly suited as a testing laboratory for studying the general problem of strongly interacting fermion systems [3,4].

The JILA experiments studied gaseous, trapped potassium- $40$ atoms in two different internal states, spin-up and spin-down (Fig. 1, inset). The effective interactions between these states are experimentally adjustable via a Feshbach resonance—a resonance of a many-body system in which a bound state is achieved under certain conditions—that can be tuned with a magnetic field. For this experiment, the detailed structure of the Feshbach resonance scattering is less important than the fact that the $s$ -wave interfermion scattering length $a$ , characterizing the interactions, can be controlled through a magnetic field $B$ . The scattering length diverges as $a \propto (B_{0} - B)^{- 1}$ near the so-called resonance position $B_{0}$ . By tuning the external magnetic field close to the resonance position, one can achieve a divergent scattering length that is much larger than the interparticle spacing ( $| a |^{3} n > > 1$ , with $n$ the fermion density), despite the fact that the effective range $r_{0}$ of the interatomic potential is quite small ( $r_{0}^{3} n < < 1$ ). This has the effect of realizing the generic and broadly applicable situation of fermions with large but short-ranged interactions.

The interfermion interactions are also attractive, so that at low temperatures and for equal densities of the up and down spin states, the system exhibits superfluidity analogous to superconductivity in a metal. Some of the key questions currently being investigated in cold-atom fermion superfluids are as follows: What is the phase diagram as a function of the large space of experimentally tunable parameters (including interactions, temperature, densities of the two fermion spin states, as well as the spatial dimensionality, which is adjustable by altering the trapping potential)? How can we observe these phases of matter in trapped dilute clouds of atoms? What can strongly interacting cold atoms tell us about other interacting fermion systems?

A few things are already known about cold-fermion superfluids, in part by analogy with superconductors, their much older electronic cousin. For example, for equal densities of the two spin states (the balanced case), the system exhibits a superfluid state at low temperature that undergoes a smooth crossover between a spin-singlet Cooper-paired Bardeen-Cooper-Schrieffer (BCS) state, when $a$ is small and negative (for $B > B_{0}$ ), to a Bose-Einstein condensate (BEC) of tightly bound molecular pairs of fermions, when $a$ is small and positive (for $B < B_{0}$ ).

However, away from these well-studied asymptotic limits the theoretical situation is much murkier. The ground state of the balanced system is believed to smoothly interpolate between the BEC and BCS limits even though the scattering length diverges at $B = B_{0}$ (called the unitary regime). This divergence frustrates standard perturbative theoretical approaches in the unitary regime. One simplification is that measurable quantities should exhibit an emergent universality [5] in the unitary regime, as their dependence on the scattering length must disappear there. However, this still leaves the difficult question of calculating these universal properties when the scattering length is not small.

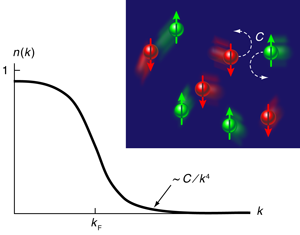
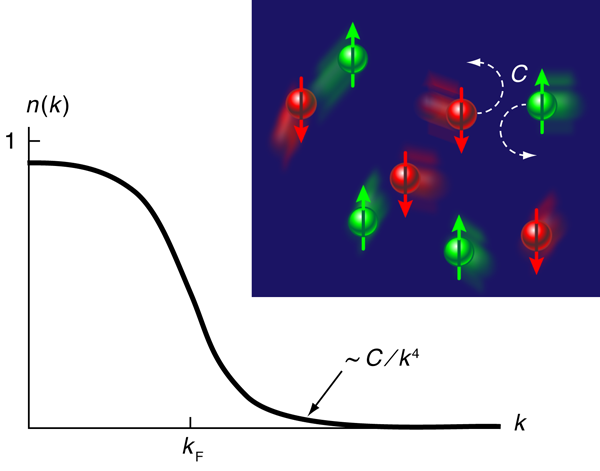
In 2008, Tan provided novel insight into this difficult problem in three sequential publications [2], which present a set of general universal relations that describe fermions with short-range interactions under a wide range of conditions, including arbitrary temperature or densities of the two spin states. Two of these universal relations are now verified experimentally by the JILA group. The Tan relations studied by the JILA team relate thermodynamic quantities to the fermion momentum distribution $n (k)$ at asymptotically large momentum $k$ (Fig. 1). The fermion momentum distribution satisfies

with $C$ , the so-called “contact,” describing the properties of such interacting fermions at short distances (i.e., as they come into contact with each other, see Fig. 1, inset). To explain the consequences of this, we will consider Tan’s ”adiabatic sweep” theorem, relating the contact to the variation of the system’s energy $E$ with inverse scattering length,

where $m$ is the fermion mass, $V$ the system volume, and $ħ$ Planck’s constant. Tan’s derivation of this formula relies on a novel and somewhat technical mathematical formalism; however, the same result has been rederived using other theoretical methods, including the operator product expansion [6], diagrammatic perturbation theory [7], and also observed in numerical computations [8].

The basic physics of Eq. (2) can be understood through an argument made by Tan [2]. Essentially, as also emphasized in Ref. [9], the true “small parameter” we need is the range $r_{0}$ of the interfermion interactions, which, in the experiment, is so small that it can be regarded as vanishing. Since fermions only interact when they occupy the same real-space position (that is, collide), if we adjust the magnitude of the interactions, altering the scattering length, the shift in the energy should reflect the probability of fermions occupying the same position, which is given by the contact. Thus, while the left side of Eq. (2) reflects many-body correlations, these correlations are completely captured by this single parameter $C$ .

The adiabatic sweep theorem applies to any two-component fermion gas with short-range interactions; however, it is particularly suited for cold atom systems that can directly control the scattering length. Testing this theorem involves two tasks: measuring the contact as defined above, and comparing to the variation of the total energy with the scattering length. For the first task, impressively, the JILA group measured the contact in three different ways. Most directly, Stewart et al. extracted the contact by measuring the momentum distribution in an expanded cloud after turning off the trapping potential and the atomic interactions (approximately, by sweeping to a magnetic field value at which the scattering length $a$ vanishes).

The other ways Stewart et al. measured the contact involve how this quantity enters other experimental observables, such as the radio-frequency (rf) spectroscopy signal [10] at large frequencies. Briefly, rf spectroscopy involves transferring atoms in one of the interacting spin states to an empty noninteracting spin state. Much like tunneling into an electronic superconductor, rf spectroscopy probes correlation effects; in particular, the large-frequency tail of the rf signal (the rate of atom transfer) varies as $1 / ω^{3 / 2}$ with a coefficient proportional to $C$ . This is the second way. Third, the JILA group has also recently developed momentum-resolved rf spectroscopy [11] for cold-atom experiments, analogous to electronic photoemission, that also probes the fermion spectral function, the occupied part of which is directly related to $n (k)$ . The three extracted values of the contact agreed with each other and with an approximate theory that interpolated known results at $T \to 0$ to estimate the expected theoretical value of the contact [12], as plotted in Fig. 2 of Ref. [1].

Here, we must note an important technical detail: The Stewart et al. experiment involving a fermion gas in a harmonic trapping potential actually extracted the trap-integrated contact, as opposed to the homogeneous-system contact that we have discussed. In this case, the corresponding energy appearing in the adiabatic sweep theorem for the trap-integrated contact involves the sum of the potential, kinetic, and interaction energies of the gas. Of these, the first contribution is obtained by observing the spatial extent of the cloud that reflects the average atom potential energy, while the remaining two contributions are obtained by measuring the total atom energy after turning off the trap and allowing expansion of the cloud.

The sum of these three contributions to the energy exhibits a variation with scattering length in accordance with the adiabatic sweep theorem, which confirms the Tan result in the limiting case of a balanced gas at low temperature across the BEC-BCS crossover. One might have worried that, since the Tan contact involves the asymptotic momentum distribution, a real experimental system may not have a large enough window to extract it. In practice, however, the asymptotic formula Eq. (1) was found to set in for wave vectors not much larger than the Fermi wave vector. Stewart et al.’s separate measurement of the internal (kinetic plus interaction) and potential energies allowed them to also verify a second Tan relation, a generalized virial theorem for a trapped fermionic gas [2]. Thus, while noninteracting fermions in a parabolic-shaped trap would satisfy the standard virial theorem equating the kinetic and potential energies, Tan’s generalized virial theorem for interacting fermions relates the difference between the internal and potential energies to a quantity proportional to the trap-integrated contact. With the confirmation of the Tan formulas, cold atomic fermions are poised to provide novel understanding of the phases and phenomena of strongly interacting fermion systems.

References

J. T. Stewart, J. P. Gaebler, T. E. Drake, and D. S. Jin, Phys. Rev. Lett. 104, 235301 (2010)
S. Tan, Ann. Phys. 323, 2952 (2008); Ann. Phys. 323, 2971 (2008); Ann. Phys. 323, 2987 (2008)
V. Gurarie and L. Radzihovsky, Ann. Phys. 322, 2 (2007)
S. Giorgini, L. P. Pitaevskii, and S. Stringari, Rev. Mod. Phys. 80, 1215 (2008)
T.-L. Ho, Phys. Rev. Lett. 92, 090402 (2004)
E. Braaten and L. Platter, Phys. Rev. Lett. 100, 205301 (2008)
R. Combescot, F.Alzetto, and X. Leyronas, Phys. Rev. A 79, 053640 (2009)
S.-Q. Su et al., Phys. Rev. A 81, 051604 (2010)
S. Zhang and A. J. Leggett, Phys. Rev. A 79, 023601 (2009)
W. Schneider and M. Randeria, Phys. Rev. A 81, 021601 (2010)
J. T. Stewart, J. P. Gaebler, and D. S. Jin, Nature 454, 744 (2008)
F. Werner, L. Tarruell, and Y. Castin, Eur. Phys. J. B 68, 401 (2009)

About the Author

Daniel Sheehy received a B.A. in physics from The Johns Hopkins University in 1995, and M.S. and Ph.D. degrees in physics from the University of Illinois in Urbana-Champaign in 1998 and 2001, respectively. After holding postdoctoral research positions at the University of British Columbia, the University of Colorado, and Iowa State University, in 2007 he arrived in Baton Rouge to become an assistant professor in the Department of Physics and Astronomy at Louisiana State University. His research interests include high-temperature superconductors, graphene, and cold atomic gases. In 2009 he was recognized as an Outstanding Referee by the American Physical Society.