Sorting superfluidity from Bose-Einstein condensation in atomic gases

Iacopo Carusotto

Viewpoint

Sorting superfluidity from Bose-Einstein condensation in atomic gases

CNR INFM-BEC Center and Dipartimento di Fisica, Università di Trento, I-38123 Povo, Italy

January 19, 2010• Physics 3, 5

With the right configuration of laser beams, researchers could measure how much of an ultracold atomic gas is actually superfluid.

Figure caption — **Figure 1:** (Left) In 1946, Andronikashvili carried out a classic experiment on superfluid liquid helium by measuring the period and damping rate of a torsional oscillator consisting of a stack of closely spaced cylindrical plates hanging by an elastic thread and immersed in the liquid helium. The normal component of the fluid was dragged along by the rotating disk surfaces, while the superfluid took no part in the rotational motion, which allowed measurement of the fraction of the superfluid component as a function of temperature (bottom panel). (Right) Cooper and Hadzibabic [2] propose an optical method to measure the superfluid fraction in ultracold atomic gases. The pair of copropagating laser beams with different orbital angular momenta create an azimuthal vector potential that imparts angular momentum to the normal component but leaves the superfluid one at rest. Spectroscopic analysis permits measurement of the induced angular momentum and hence the amount of normal vs superfluid gas.

More than 70 years after its first discovery, superfluidity is still challenging researchers to unveil its most subtle aspects [1]. Among its many odd properties, a superfluid is characterized by a zero viscosity, i.e., the ability to flow without apparent friction. Long after the pioneering observations of these effects in liquid helium in the 1930s and 1940s, the development of laser cooling techniques for atomic gases has offered experimentalists a new framework for investigating the fundamental concepts of superfluidity and its not-so-direct relation with Bose-Einstein condensation. Writing in Physical Review Letters, Nigel Cooper and Zoran Hadzibabic from Cambridge University, UK, now propose [2] a novel protocol to experimentally address superfluidity in gases of ultracold atoms independently from condensation. Application of this method to strongly correlated atomic Fermi gases with nontrivial pairing mechanisms [3] will hopefully contribute to our understanding of puzzling condensed matter phenomena such as high-temperature superconductivity.

Soon after the first observations, Fritz London proposed that Bose-Einstein condensation—the phenomenon in which bosons below a transition temperature accumulate into a single one-particle quantum state—might be responsible for superfluidity of liquid helium. Several decades elapsed before London’s hypothesis got a direct experimental verification from the measurement of the momentum distribution by means of neutron scattering experiments [4]: even at the lowest temperatures where the superfluid fraction is almost $100 %$ , the strong correlations between the atoms forming the liquid deplete the population of the Bose-Einstein condensate state to only $10 %$ of the total mass.

The situation is substantially different in dilute ultracold atomic gases. At low temperatures, such gases are in fact almost fully condensed and superfluid, but a conceptual difference still exists between the two properties. Researchers now routinely measure the condensate fraction by looking at the velocity distribution in time-of-flight images, but some conceptual aspects of superfluidity are still awaiting experimental investigation. In contrast to the complex microscopic structure of liquid helium, the simplicity of the theoretical description of dilute atomic gases allows a deep understanding of the basic mechanisms underlying superfluidity phenomena in simple terms.

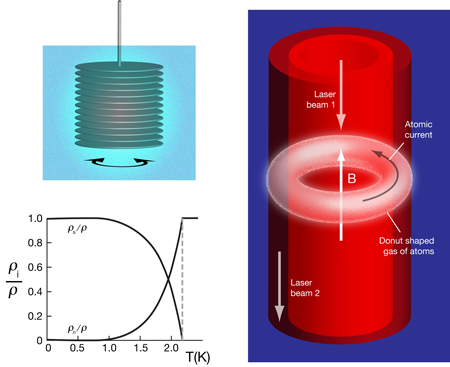
One of the neatest formulations of the concept of superfluidity involves the response of the fluid to rotation in the so-called “rotating bucket experiment”: while the normal component of the fluid is dragged by the bucket, the superfluid component is almost unaffected by the rotating walls [1]. This idea was first put into practice in 1946 by Andronikashvili using a torsional oscillator and a bulk three-dimensional sample of liquid helium (see Fig. 1, left panel): the appearance of a superfluid is detected by the drop in the moment of inertia [5]. Interesting measurements of the reduced moment of inertia of atomic Bose-Einstein condensates have been performed by looking at the frequency of the so-called scissors mode in an anisotropic trap and at the time evolution of the shape of an expanding condensate after releasing the trap [6].

The definition of superfluid fraction can be formulated in a formal and quantitative way in terms of the response of the fluid to an external vector field [7]. If placed in a rotating trap, neutral atoms behave in fact as if they were subject to a constant magnetic field parallel to the rotation axis; in this picture, the absence of response to rotation is the superfluid analog of the Meissner effect of superconductors in which magnetic fields are excluded from the material. Along these lines, it was soon recognized that the study of the response of the gas to artificial magnetic fields may offer a much wider range of experimental possibilities to investigate superfluidity.

The idea of creating artificial magnetic fields for neutral atoms dates back to the work of Dum and Olshanii [8] and is based on the Berry phase that is accumulated along an adiabatic closed contour in real space. In the case of three-level atoms, two coherent laser beams can be used to drive the atoms into a state that does not couple directly to the light field (a so-called “dark” state) via a coherent population trapping mechanism. The energy separation between the dark and bright states guarantees adiabaticity if the atomic motion is slow enough. The vector potential $A$ associated to the spatial dependence of the dark state can be designed via the geometries and the time-dependence of the laser beams. The resulting magnetic field $B = \nabla \times A$ imposes a force on the neutral atoms analogous to the Lorentz force on charged particles. The efficiency of this approach to manipulate Bose-Einstein condensates has been recently verified with the observation of quantized vortices for large enough values of the applied effective magnetic field [9].

The paper by Cooper and Hadzibabic investigates this physics in a ring-shaped geometry where three-level atoms are dressed by a pair of specially tailored copropagating optical beams carrying orbital angular momentum (see Fig. 1, right panel). This configuration creates an azimuthal vector potential that winds around the ring. Once the atoms have thermalized in the presence of the magnetic field, the induced current pattern is used to assess the superfluidity of the cloud: if this is normal, a rotational momentum pattern will be created in the gas; if the cloud is instead superfluid, the atoms will preserve their original zero value of the momentum. A simple way of reading out the atomic momentum is provided by the strong dependence of the dark state wave function on momentum value: the differential population of the different spin states is proportional to the normal, nonsuperfluid fraction.

The simplicity of Cooper and Hadzibabic’s proposal suggests an extreme flexibility in its application to a number of physical situations. Although the paper discusses the simplest case of Bose systems in a multiply-connected geometry, no difficulties appear to prevent the proposal from being combined with the great tunability of system parameters that characterizes atomic systems, such as the interaction strength, the dimensionality, and even the quantum statistics of the atomic constituents. In many cases, a measurement of the superfluid fraction will be a crucial complement to standard observables such as density profiles and time-of-flight images after switching off the trap.

A most relevant system where such issues are presently under active investigation is quasi-two-dimensional Bose gases. A remarkable recent experiment [10] has extracted information on the spatial coherence of the atomic matter field by letting a pair of two-dimensional clouds interfere. Even though it has demonstrated the transition from an exponential to a power-law decay of the long-distance coherence, such an experiment can hardly detect the universal jump in the superfluid fraction that characterizes the so-called Berezinskii-Kosterlitz-Thouless transition [11]. The method proposed by Cooper and Hadzibabic appears to be an ideal tool to assess superfluidity independently of condensation and coherence. In the future, such techniques are expected to be of great use in identifying the different phases of strongly correlated atomic Fermi gases where superfluidity may arise from nontrivial order parameters that are not detectable in coherence experiments.

The concept of superfluidity is not limited to systems at or close to thermodynamic equilibrium, however. Very recently, experiments on quantum degenerate gases of exciton-polaritons in semiconductor planar microcavities have started exploring many-body physics in a regime where the standard concepts and tools of statistical mechanics cannot be straightforwardly applied. An external pump is in fact needed to compensate losses due to the very short polariton lifetime and the nonequilibrium stationary state is determined by a dynamical balance of pumping and losses [12]; this fact, rather than a hindrance as initially believed, is nowadays leading to interesting new physics. Bose-Einstein condensation of polaritons has been demonstrated from the long-range coherence of the emitted light [13], and the superfluidity properties of these nonequilibrium polariton gases are presently attracting a strong interest in both the experimental [14] and the conceptual points of view [15]. To put these investigations on a quantitative level, protocols to directly measure the superfluid fraction independently of condensation will be of extreme utility.

References

A. J. Leggett, Rev. Mod. Phys. 71, S318 (1999)
N. R. Cooper and Z. Hadzibabic, Phys. Rev. Lett. 104, 030401 (2010)
I. Bloch, J. Dalibard, and W. Zwerger, Rev. Mod. Phys. 80, 885 (2008); S. Giorgini, L. P. Pitaevskii, and S. Stringari, 80, 1215 (2008)
P. E. Sokol, in Bose-Einstein Condensation, edited by A. Griffin, D. W. Snoke, and S. Stringari (Cambridge University Press, Cambridge, 1995), p. 51[Amazon][WorldCat]
E. L. Andronikashvili and Yu. G. Mamaladze, Rev. Mod. Phys. 38, 567 (1966)
O. M. Maragò, S. A. Hopkins, J. Arlt, E. Hodby, G. Hechenblaikner, and C. J. Foot, Phys. Rev. Lett. 84, 2056 (2000); G. Hechenblaikner, E. Hodby, S. A. Hopkins, O. M. Maragò, and C. J. Foot, 88, 070406 (2002)
D. Pines and Ph. Nozières, The theory of quantum liquids (Benjamin, New York, 1966)[Amazon][WorldCat]
R. Dum and M. Olshanii, Phys. Rev. Lett. 76, 1788 (1996)
Y.-J. Lin, R. L. Compton, K. Jiménez-García, J. V. Porto, and I. B. Spielman, Nature 462, 628 (2009)
Z. Hadzibabic, P. Krüger, M. Cheneau, B. Battelier, and J. Dalibard, Nature 441, 1118 (2006)
P. Minnhagen, Rev. Mod. Phys. 59, 1001 (1987)
B. Schmittmann and R. K. P. Zia, in Phase Transitions and Critical Phenomena, edited by C. Domb and J. Lebowitz (Academic Press, New York, 1995), Vol. 17[Amazon][WorldCat]
J. Kasprzak et al., Nature 443, 409 (2006)
A. Amo, J. Lefère, S. Pigeon, C. Adrados, C. Ciuti, I. Carusotto, R. Houdré, E. Giacobino, and A. Bramati, Nature Phys. 5, 805 (2009); D. Sanvitto, F. M. Marchetti, M. H. Szymanska, G. Tosi, M. Baudisch, F. P. Laussy, D. N. Krizhanovskii, M. S. Skolnick, L. Marrucci, A. Lemaitre, J. Bloch, C. Tejedor, and L. Viña, arXiv:0907.2371
I. Carusotto and C. Ciuti, Phys. Rev. Lett. 93, 166401 (2004); M. H. Szymanska, J. Keeling, and P. B. Littlewood, 96, 230602 (2006); M. Wouters and I. Carusotto, arXiv:1001.0660; J. Keeling and N. Berloff, Nature 457, 273 (2009)

About the Author

Iacopo Carusotto completed his Ph.D. in 2000 at Scuola Normale Superiore in Pisa, Italy, and then carried out postdoctoral work at Kastler-Brossel Laboratory of École Normale Supérieure in Paris. Since 2003, he has been a researcher at the INO-CNR BEC Center in Trento, Italy. He has been an associated researcher for CNRS in France and a visiting professor at the Swiss Federal Institute of Technology (ETH) in Zurich. His primary scientific interests include quantum fluids of light (from superfluid light to strongly correlated photon gases), topological photonics and physics, and the study of analogs of gravitational phenomena in atomic and optical systems.