Liberating anyons from two dimensions

Ady  Stern; Michael Levin

Viewpoint

Liberating anyons from two dimensions

Department of Condensed Matter Physics, Weizmann Institute of Science, Rehovot, Israel 76100
Physics Department, Harvard University, Cambridge, MA 02138, USA

January 25, 2010• Physics 3, 7

The combination of trivial and topological band insulators with a superconductor is bringing anyons—particles that behave neither according to purely Bose nor Fermi statistics—into the three-dimensional world.

Animation: Alan Stonebraker

Video 1: A cartoon that demonstrates how the concept of Majorana fermions—

2 D

objects—can be realized in a

3 D

space. The

2 D

bubbles are defined by superconducting surfaces that separate trivial and topological insulators. The red vortex lines are the lines around which the phase of the electron pairing order parameter winds. Majorana fermions are localized at the points where vortex lines pierce a superconducting surface. The upper right bubble and animation exemplify how the state of the system may change without a Majorana fermion being moved: The bubble connects to its neighbor via a narrow (Josephson) junction. If the vortex line is rotated around the bubble, it goes through the Josephson junction, and a unitary transformation is applied on the state of the system, but the Majorana fermions are still in their original positions.

A paper appearing in Physical Review Letters [1] from Jeffrey Teo and Charles Kane at the University of Pennsylvania, US, is part of an ongoing attempt [2] to go beyond the fermion-boson dichotomy and find other types of quantum statistics. While this attempt has been successful in systems of two spatial dimensions ( $2 D$ ), mostly in the context of the quantum Hall effect [3,4], it is widely believed to be impossible to realize in three dimensions ( $3 D$ ). Teo and Kane’s paper specifically addresses the $3 D$ case. While their discussion is highly theoretical, it is of interest to a wide range of fields of physics, such as many-body condensed matter systems, quantum computation, and the fundamentals of quantum mechanics.

Let us first ground the notion of the interchange of identical particles in something physical, rather than mathematical. Imagine two “buckets,” each of which contains one of two identical particles. If the ground state of the system is separated from the excited states by an energy gap, and the motion of the buckets is slow, then the system will not be excited by interchanging the position of the buckets. We can then look at effects that are associated solely with the interchange of the particles, that is, effects that depend on the topology of the trajectory along which the particles move, and are independent of its geometry and time dependence.

We can formally analyze these effects by defining the Hamiltonian of this system in such a way that a bucket traps the object whose quantum statistics we want to calculate. This object may be the elementary particle that makes up the system, or it may be a collective excitation, such as a quasiparticle or a vortex in a fluid. We carry out the interchange of two particles by moving the buckets slowly along a trajectory that ends with their initial positions interchanged. If the ground state is nondegenerate, the only effect of this interchange is a phase factor, and this phase may be calculated by the usual formalism for an adiabatic evolution.

This discussion, however, calls for a distinction between $2 D$ and $3 D$ . Let us think about two consecutive interchanges of the same two buckets, i.e., of trajectories in which two buckets first interchange positions, and then go back to their initial locations. In $3 D$ , all such trajectories are topologically equivalent, and are equivalent to not even moving the buckets. The topological phase associated with two interchanges must then be a multiple of $2 π$ , giving us the usual boson/fermion dichotomy. In $2 D$ , however, after two buckets interchange positions, they can come back to their original positions by retracing their steps, or by completing one winding around one another. These two trajectories are topologically distinct, and cannot be deformed into one another without the buckets touching each other. Thus they may be associated with two different topological phases. The phases may in fact take any value, which is why these $2 D$ particles are called “anyons.”

If the ground state of the system is degenerate, a slow interchange can do more than just multiply the ground state by a phase; it may take the system from one ground state to another [4–8]. Expressed mathematically, such an interchange multiplies the ground state by a unitary matrix that operates within the subspace of degenerate ground states. Unitary matrices are noncommutative under multiplication, and hence the anyons become non-Abelian: the final state they reach after a series of interchanges depends on the order at which these interchanges are carried out. Important as this difference is, however, it does not seem to affect the distinction between $2 D$ and $3 D$ . Anyons, be they Abelian or non-Abelian, seem to exist only in $2 D$ .

The paper by Teo and Kane questions this well accepted constraint, and aims to liberate anyons, specifically non-Abelian anyons [4–8], from the confinements of $2 D$ . The source of inspiration is the interface between a trivial insulator and what is called a topological insulator [9–11]. Of the various properties of these insulators, we only need to note that the two insulators are characterized by an energy gap separating their respective ground states from the rest of their spectra, while the interface between them is a $2 D$ metal. Teo and Kane consider a scenario where there is an attractive pairing interaction between the electrons, so that this metal becomes a superconductor with an energy gap in its quasiparticle spectrum. Applying a magnetic field will then introduce vortices into this superconductor. It turns out that these vortices are non-Abelian anyons, as we now explain.

In general, superconductivity vanishes at the cores of vortices, leading to localized excitations at energies lower than the energy gap at the bulk of the superconductor. For some superconductors, including the one we described above, each vortex carries one excitation mode exactly at zero energy. As for all excitations of a superconductor, the operator that creates this mode is a superposition of creating and annihilating a fermion. Uniquely for the zero energy mode, the creation part is the Hermitian conjugate of the annihilation part, making the mode a “Majorana fermion” [7,8,12,13]. The presence of these modes makes the ground state degenerate. Importantly for us, the fermionic operator that describes each of these Majorana fermions depends on the phase configuration of the superconducting order parameter around the vortex in which it is localized. As one vortex is taken to wind around another, the phase of the order parameter around each of the two vortices winds by $2 π$ . For the Cooper pairs that make up the superconductor this is an unobservable winding, but the Majorana fermion operators are multiplied by an observable factor of $- 1$ . Thus the winding operation applies a unitary transformation on the ground state of the superconductor; the vortices are non-Abelian anyons. (An interchange of two vortices is associated with a similar, but slightly more complicated unitary transformation.)

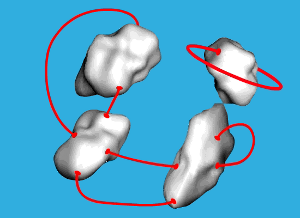
Imagine now that we fill a three-dimensional space with a trivial insulator, and that we have a “control panel” that allows us to switch the trivial insulator into a topological one at any position we wish. In practice, this switch might be a change in the lattice structure that we can induce, for example, by applying pressure. Moreover, imagine that the electrons have an attractive pairing interaction everywhere, so that a superconductor is formed wherever we create an interface between a topological and a trivial insulator. As a result, by choosing the regions in which we switch the insulator to its topological state, we can form blocks of topological insulator, each wrapped by a two-dimensional superconducting shell. In addition, by applying a magnetic field we can make vortices pierce the superconductors. Altogether, the $3 D$ space will consist of some arrangement of $2 D$ superconducting bubbles and $1 D$ vortex lines (see Video 1). The vortex lines are the lines around which the phase of the order parameter that characterizes the pairing interaction winds.

Vortex lines that pierce a superconducting bubble create an equal number of $2 D$ vortices and antivortices, and each of these carry a single Majorana fermion. The Majorana fermions make the ground state degenerate. If we interchange two vortices on the same bubble we get the $2 D$ non-Abelian statistics that we discussed earlier. It turns out that for $2 N$ Majorana fermions on a bubble, the number of ground states is $2^{N - 1}$ . Thus for the non-Abelian statistics to be manifested on a single bubble, at least four vortices, each carrying a single Majorana fermion (such as either of the two bubbles at the bottom of Video 1), should be present.

Interchanging vortices on the same bubble is really a $2 D$ operation—what makes the story “ $3 D$ ” is that we can interchange vortices on different bubbles. All we need is a little help from our control panel. To make such an interchange we deform the two bubbles until they touch one another—making, in effect, a Josephson junction—and then merge them into one (as in Video 1, where the two bubbles on the right are just touching). Now that we have the two vortices on the same $2 D$ manifold, they can interchange. After they interchange we bring the system back to its original form: we cut and paste the vortex lines within the bubble such that they get back to their original configuration, we break the bubble back into two, and we deform the two bubbles into their original shapes. The configuration of bubbles and vortex lines is now back to where we started from, but two Majorana fermions have interchanged. In this scheme we can interchange any two Majorana fermions within the $3 D$ space, and have the system transform from one ground state to another, just as we did with non-Abelian anyons in $2 D$ .

In fact, we can apply a unitary transformation that takes the system from one ground state to another without even moving the Majorana fermions. The Majorana fermions occur at the intersection of the $2 D$ superconducting bubbles with the $1 D$ vortex lines. Imagine a bubble pierced by a vortex line that closes outside of the bubble to form a vortex loop (see the upper right bubble in Video 1). The vortex loop is split into two parts, one inside the sphere and one outside of it. If we take the external part of the loop and move it around the superconducting bubble (see animation Video 1), we wind the relative phase of the bubble’s order parameter by $2 π$ , relative to the phase of all the other bubbles. If we make the phases of the order parameters on the various bubbles all locked to one another by interconnecting the bubbles by Josephson junctions, the $- 1$ factor that this winding applies to the Majorana fermions of the bubble will apply a unitary transformation on the state of the system, even though none of the Majorana fermions has moved.

As this last setup clarifies, a description of the system in terms of point particles (e.g., Majorana fermions) living in a $3 D$ world should be formulated with great care, since the time evolution of the system cannot be fully defined in terms of the trajectories of these particles alone. What is the most general and concise way to describe systems of these types is one of several questions raised by Teo and Kane’s paper. These questions are likely to be at the center of future works, motivated both by their relevance to fundamental aspects of quantum mechanics and by their possible relevance to condensed matter systems [14,15].

References

J. C. Y. Teo and C. L. Kane, Phys. Rev. Lett. 104, 046401 (2010)
F. Wilczek, Fractional statistics and anyon superconductivity (World Scientific, Singapore, 1990)[Amazon][WorldCat]
A. Stern, Ann. Phys. 323, 204 (2008)
Chetan Nayak, Steven H. Simon, Ady Stern, Michael Freedman, and Sankar Das Sarma, Rev. Mod. Phys. 80, 1083 (2008)
G. Moore and N. Read, Nucl. Phys. B 360, 362 (1991)
C. Nayak and F. Wilczek, Nucl. Phys. B 479, 529 (1996)
N. Read and D. Green, Phys. Rev. B 61, 10267 (2000)
D. A. Ivanov, Phys. Rev. Lett. 86, 268 (2001)
L. Fu, C. L. Kane, and E. J. Mele, Phys. Rev. Lett. 98, 106803 (2007)
J. E. Moore and L. Balents, Phys. Rev. B 75, 121306 (2007)
X. L. Qi, T. L. Hughes, and S.-C. Zhang, Phys. Rev. B 78, 195424 (2008)
Frank Wilczek, Nature Phys. 5, 614 (2009)
Liang Fu and C. L. Kane, Phys. Rev. Lett. 100, 096407 (2008)
Liang Fu and C. L. Kane, Phys. Rev. Lett. 102, 216403 (2009)
J. Nilsson, A. R. Akhmerov, and C. W. Beenakker, Phys. Rev. Lett. 101, 120403 (2008)

About the Authors

Ady Stern is a professor of physics at the Weizmann Institute of Science, in Rehovot, Israel. He received his Ph.D. from Tel-Aviv University, and was a Junior Fellow at Harvard. His research focuses on the quantum Hall effect, non-Abelian states of matter, and mesoscopic physics. He is also interested in the popularization of science.

Michael Levin received his Ph.D. from MIT in 2006. He is currently a Junior Fellow at the Harvard Society of Fellows. He is particularly interested in topological aspects of quantum condensed matter physics.