Jumping from two and three particles to infinitely many
Often the few-body and the many-body worlds are, figuratively speaking, worlds apart. For example, the binding energies of the helium- 4 dimer and the helium- 4 trimer are about 0.001K and 0.1K, respectively [1]. The binding energy per particle Eb in the large particle limit, i.e., the binding energy per particle of the homogeneous or bulk system, in contrast, is much larger: Eb≈7K [2]. This suggests that the binding energy of the bulk system cannot be predicted on the basis of just the two-particle and the three-particle energies. Indeed, it is found that a quantitatively correct prediction of the binding energy of the bulk requires knowledge of the energies of clusters with up to hundreds of atoms [2].
In an elegant sequence of papers, the first published in 2009 in Physical Review Letters [3] with follow-ups now appearing in Physical Review A [4] and Physical Review B [5], Xia-Ji Liu, Hui Hu, and Peter Drummond of the Swinburne University of Technology in Melbourne, Australia, have predicted the thermodynamic properties of two- and three-dimensional two-component Fermi gases down to unexpectedly low temperatures, purely on the basis of the solutions of just the two-body and the three-body problem. A detailed theoretical analysis, together with an analysis of a set of impressive experimental data for three-dimensional gases [6,7], provides strong evidence that the approach pursued by Liu and co-workers correctly describes the key physics in a quantitative way. Given the above helium example, though, it seems counterintuitive that knowledge of the two-body and three-body energy spectra is all that is needed. Viewed from this perspective, the work by Liu and co-workers is a beautiful contribution that bridges the few-body and the many-body worlds. Furthermore, it makes an important leap toward determining the equation of state of two-component Fermi gases at any temperature, any interaction strength, and any dimensionality.
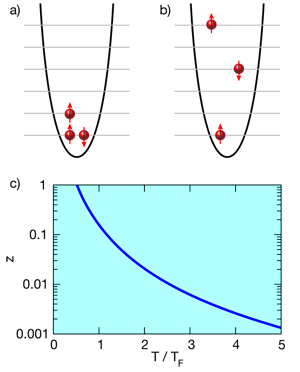
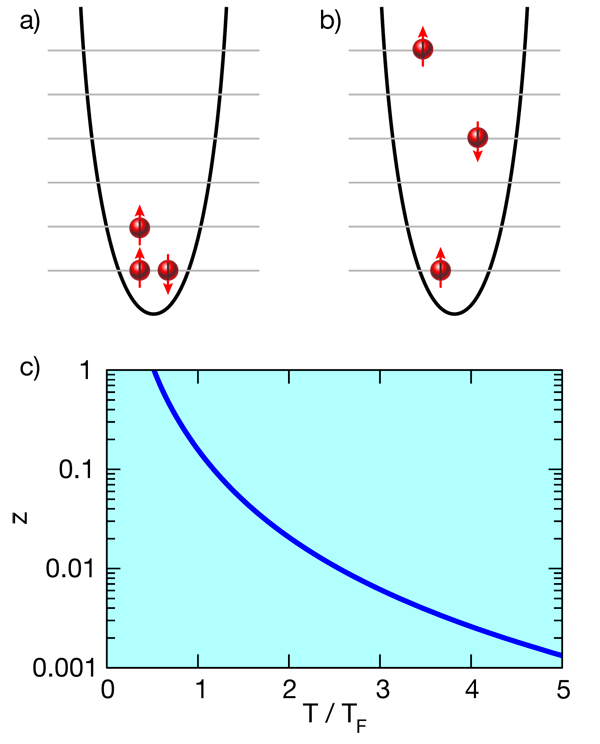
The basic constituents of two-component gases are fermionic atoms, such as lithium- 6 or potassium- 40, in two different hyperfine states. The mixture of atoms can be thought of as a pseudo-spin- 1/2 system, where atoms in one hyperfine state are considered “spin up” and those in the other hyperfine state are “spin down.” Liu and co-workers [3,4] assume a 50-50 mixture of spin-up and spin-down atoms, with equal masses, in three spatial dimensions. An intriguing feature of ultracold atomic gases is their large de Broglie wavelength λ=h/p, where h denotes Planck’s constant and p the momentum. In practice, the de Broglie wavelength is increased by decreasing the sample’s temperature T ( λ∝1/√T). As is well known from textbook statistical mechanics [8], a Bose gas undergoes a transition to a unique state of matter, a Bose-Einstein condensate, when the de Broglie wavelength becomes of the order of the interparticle spacing. In fermionic systems, however, the situation is different. Because of the Pauli exclusion principle, the atomic Fermi gas cannot undergo condensation like a Bose gas but instead becomes Fermi degenerate when the de Broglie wavelength becomes sufficiently large. Below the degeneracy temperature TF, nearly all available energy levels are filled [as indicated in the cartoon in Fig. 1(a)].
Currently, a major quest in the field of cold atom physics is the accurate determination of finite-temperature thermodynamic quantities such as the energy, entropy, and chemical potential. Possibly the most straightforward approach to obtain these observables is to simulate the N-body problem. Of course, any such treatment requires integrating over 3N degrees of freedom, a task that can, in general, only be performed through Monte Carlo sampling. For fermions, however, Monte Carlo approaches are, except for a few fortuitous exceptions, plagued by the so-called sign problem [9], posing severe limitations on the applicability of this approach. Alternatively, one might think of employing an approach that expands around a small parameter, as did Liu and co-workers: They pursued a cluster, or virial, expansion approach [8], which treats the N-body problem in terms of one-body, two-body, three-body and so on clusters or subsystems. In particular, the thermodynamic potential Ω, Ω∝Σnbnzn (here, n labels the cluster), is expanded in terms of the fugacity z, which is a small parameter at large T but increases with decreasing T [see Fig. 1(c)]. The expansion in terms of z is equivalent to an expansion in terms of the “diluteness parameter” ρλ3 [8], where ρ is the density and λ the de Broglie wavelength, which increases with decreasing T. The nth virial coefficient bn is determined by the energy spectrum of the nth cluster; naturally, the determination of the virial coefficients becomes significantly more involved as n increases. At low T (large z), where only the lowest energy levels are filled [Fig. 1(a)], one needs the lowest portion of the energy spectrum of many clusters. At high T (small z), where more of the higher energy levels are occupied [Fig. 1(b)], one needs a large portion of the energy spectrum of just the smallest clusters. A natural question is thus how many clusters, and how much of their energy spectrum, are needed to describe the particularly interesting regime in the vicinity of the temperature where the Fermi gas becomes degenerate.
Liu and co-workers found that it is sufficient to treat the two-body and the three-body problem [3,4], that is, the second and third terms in the virial expansion. To elucidate how to calculate the energy spectra of the two-body and three-body systems, let us return to the de Broglie wavelength. The de Broglie wavelength not only determines the degeneracy temperature of Bose and Fermi gases, but also sets a “resolution limit” when two atoms collide. Much like in a light microscope, two colliding atoms can only probe those features of the underlying interaction potential that are of the order of, or larger than, the de Broglie wavelength. This is a key ingredient to Liu and co-workers’ successful treatment. In the temperature regime of interest, “head-on” s-wave collisions between spin-up and spin-down atoms dominate and higher partial wave contributions are strongly suppressed [10]. Motivated by the microscope resolution analogy, these s-wave collisions can be treated by replacing the true atom-atom interaction potential by a simple short-range boundary condition on the wave function, which encapsulates the “net effect” of the true atom-atom potential. This replacement is designed to leave the low-energy atom-atom phase shift, which determines many observables of trapped cold atom gases, unchanged. However, it eliminates all the unwanted high-energy physics, thereby tremendously simplifying the theoretical treatment of the problem. Interestingly, these ideas go back to Fermi’s groundbreaking 1934 paper on the scattering between slow neutrons and bound hydrogen atoms [11].
Replacing the true atom-atom interactions by properly chosen boundary conditions, the quantum mechanical two-particle and three-particle systems become soluble. As has been shown in Busch et al.’s seminal work [12], the determination of the two-particle energy spectrum reduces to finding the roots of a simple transcendental equation. The determination of the three-body energy spectrum is more involved and several approaches exist. Among these, the approach put forward by Kestner and Duan [13], and subsequently refined by Liu and co-workers [3,4], is particularly appealing since it allows for an efficient and accurate determination of essentially the entire energy spectrum for any interaction strength. Equipped with the two-body and the three-body energy levels, Liu and co-workers calculated the virial coefficients b2 and b3, and determined—using the thermodynamic potential Ω—observables such as the entropy for large samples of trapped two-component Fermi gases as a function of the temperature.
Building upon the results by Liu and co-workers, Salomon’s group extracted the fourth-order virial coefficient from experimental data [7]. This analysis confirmed that much of the thermodynamics is determined by the second and third virial coefficients, at least down to temperatures around the degeneracy temperature.
The work by Liu and co-workers beautifully demonstrates how accurate solutions of the few-body problem also provide a great deal of insight into the many-body problem. The work has already had a profound impact on determining the equation of state of s-wave interacting Fermi gases in three dimensions. Moreover, the framework has been extended to predict thermodynamic properties of strictly two-dimensional Fermi gases [5], which can be realized experimentally with present-day technology. It would be interesting to extend the treatment of Liu and co-workers to systems that live in mixed dimensions [15], where, say, the spin-up atoms move in three spatial dimensions and the spin-down atoms move in two spatial dimensions. In such a system, the spin-up atoms move freely in the third spatial dimension and interact with the spin-down atoms only when they pass through the plane in which the spin-down atoms live. Finally, another open challenge is the finite-temperature treatment of two-component Fermi gases with unequal masses. For these problems, as well as others, Liu et al.’s calculations should provide a solid jumping off point.
References
- see, e.g., B. D. Esry, C. D. Lin, and C. H. Greene, Phys. Rev. A 54, 394 (1996); R. E. Grisenti, W. Schöllkopf, J. P. Toennies, G. C. Hegerfeldt, T. Köhler, and M. Stoll, Phys. Rev. Lett. 85, 2284 (2000)
- V. R. Pandharipande, J. G. Zabolitzky, S. C. Pieper, R. B. Wiringa, and U. Helmbrecht, Phys. Rev. Lett. 50, 1676 (1983)
- X.-J. Liu, H. Hu, and P. D. Drummond, Phys. Rev. Lett. 102, 160401 (2009)
- X-J. Liu, H. Hu, and P. D. Drummond, Phys. Rev. A 82, 023619 (2010)
- X-J. Liu, H. Hu, and P. D. Drummond, Phys. Rev. B 82, 054524 (2010)
- L. Luo, B. Clancy, J. Joseph, J. Kinast, and J. E. Thomas, Phys. Rev. Lett. 98, 080402 (2007)
- S. Nascimbene, N. Navon, K. J. Jiang, F. Chevy, and C. Salomon, Nature 463, 1057 (2010)
- see, e.g., and D. A. McQuarrie, Statistical Mechanics (University Science Books, Sausalito, 2000)[Amazon][WorldCat]
- M. Troyer and U.-J. Wiese, Phys. Rev. Lett. 94, 170201 (2005)
- H. A. Bethe, Phys. Rev. 47, 747 (1935); E. P. Wigner, 73, 1002 (1948)
- E. Fermi, Nuovo Cimento 11, 157 (1934)
- T. Busch, B.-G. Englert, K. Rzazewski, and M. Wilkens, Found. Phys. 28, 549 (1998)
- J. P. Kestner and L.-M. Duan, Phys. Rev. A 76, 033611 (2007)
- G.-B. Jo, Y.-R. Lee, J.-H. Choi, C. A. Christensen, T. H. Kim, J. H. Thywissen, D. E. Pritchard, and W. Ketterle, Science 325, 1521 (2009)
- Y. Nishida and S. Tan, Phys. Rev. Lett. 101, 170401 (2008); G. Lamporesi, J. Catani, G. Barontini, Y. Nishida, M. Inguscio, and F. Minardi, 104, 153202 (2010)