Clues from a rare decay

Gino Isidori

Viewpoint

Clues from a rare decay

Laboratori Nazionali di Frascati, C.P. 13, I-00044 Frascati, Rome, Italy

February 22, 2011• Physics 4, 15

An ideal place to look for new physics beyond the standard model is a rare particle decay, and new calculations are providing a highly accurate picture of what to expect.

Figure caption — **Figure 1:** (Top) $K \to π ν \bar{ν}$ decays are mediated by the flavor-changing neutral-current transition $s \to d ν \bar{ν}$ (here $s$ and $d$ stand for strange and down quarks). (Bottom) Representative one-loop diagrams contributing to the $s \to d ν \bar{ν}$ amplitude within the standard model (left) and within an extension of the standard model (right).

According to the standard model of particle physics, matter consists of three “families” of quarks and leptons. Each family contains four types of particles: two quarks and two leptons. Ordinary matter consists essentially of particles of the first family: the up and down quarks, which are strongly bound inside protons and neutrons; the electrons; and the electron-neutrinos, which are abundantly produced by fusion reactions inside stars. As far as we know, quarks and leptons of the second and third family are identical copies of those in the first family, but they have heavier masses. These heavy quarks and charged leptons are unstable particles that can be produced in high-energy collisions, but decay extremely rapidly, via the weak interaction, into particles of the first family.

This description of matter is consistent with what experiments have observed, but why we have three almost identical replicas of quarks and leptons (also referred to as three “flavors” of quarks and leptons), only with different masses, is one of the big open questions in particle physics. In the limit of unbroken electroweak symmetry, none of the particles of the standard model should have a mass. The problem of quark and lepton masses is therefore intimately related to the other big open question in particle physics: why do the carriers of the weak force—the $W$ and $Z$ bosons—have mass? Within the standard model, these two problems are both solved by what is called the Higgs mechanism: quarks and leptons, as well $W$ and $Z$ bosons, have a mass because they interact with a new type of field, called the Higgs field. In this picture, it is the Higgs field that breaks electroweak symmetry. If high-energy experiments at the Large Hadron Collider (LHC) at CERN can detect an excitation of the Higgs field—the Higgs particle—they would provide proof that this mechanism underlies the masses of existing particles.

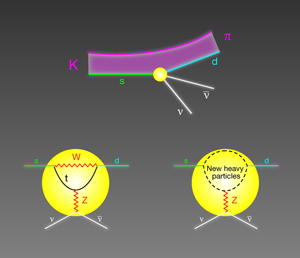
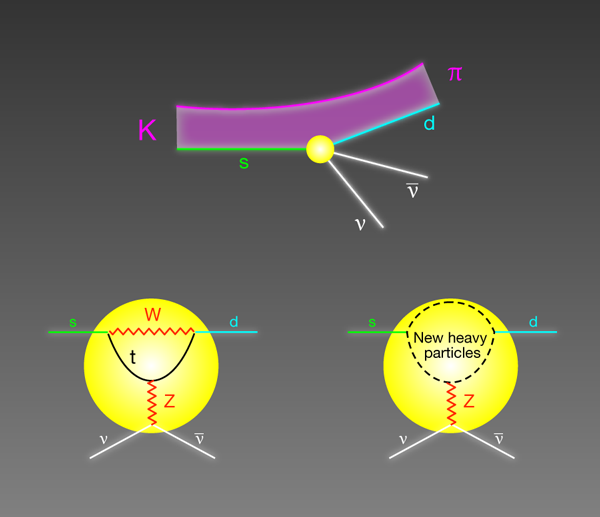
The Higgs mechanism postulated within the standard model is, however, not satisfactory for various reasons, most notably because it becomes unstable at high energies. Instead, it is likely that the idea of a Higgs field is really only a low-energy approximation of a more fundamental theory. Signatures of this “true” theory would appear at higher energies as new degrees of freedom in the form of new heavy particles. Attempts to find evidence of this new theory can be divided into two main categories: (i) Direct searches for the new degrees of freedom via experiments at the high-energy frontier, and in particular at the LHC; and (ii) indirect searches for the new particles via precision studies at low energies, the so-called high-intensity frontier. The latter is particularly relevant to determine the flavor structure of the new degrees of freedom, or how these new fields couple to the different families of quarks and leptons. It is within this context that Joachim Brod, Martin Gorbahn, and Emmanuel Stamou at the Technical University of Munich, Germany, have worked out an improved theoretical description of a rare particle decay that will give experimentalists a powerful tool to look for signs of a more fundamental theory [1]. Their calculations, which specifically detail the probability that a $K$ meson (kaon) decays into pion, neutrino, and antineutrino particles ( $K \to π ν \bar{ν}$ ) (see Fig. 1), are presented in Physical Review D.

Assuming it is the correct picture, the presence of the Higgs field mixes different quark families under weak interactions and sets a hierarchy in the various decay modes of the heavier quarks into the lighter ones. In particular, the interplay of weak and Higgs interactions implies that processes where a quark changes its flavor but not its charge (e.g., the strange quark belonging to the second family is transformed into the down quark of the first family, which has different mass but the same electric charge) can occur only at higher orders in the electroweak interactions and are strongly suppressed. These processes, called flavor-changing neutral-current (FCNC) transitions, are an ideal place to look for new physics: the signal (new physics) will stand out prominently against the small background of what is already predicted by the standard model.

The $K \to π ν \bar{ν}$ decays that Brod et al. study are a particularly interesting example of FCNC transitions: the probability for these processes to occur (so-called branching ratios) can be computed to an exceptionally high degree of precision, not matched by any other FCNC process involving quarks. The exceptional theoretical cleanness of $K \to π ν \bar{ν}$ decays within the standard model has a simple origin: the probability of the decays is dominated by the exchange of the heaviest standard model particles (top-quark, $W$ and $Z$ bosons) and these contributions can be computed reliably in perturbation theory. Starting in the early nineties, theorists began making these calculations increasingly precise [2]. Bord et al. [1] further reinforce the theoretical cleanliness of these modes with a complete evaluation of the two-loop electroweak contributions (i.e., including contributions up to the sixth order in the weak coupling constant). As discussed in Ref. [1], the present irreducible theoretical errors on the branching ratios are at the level of $4 %$ and $3 %$ for the $K^{+} \to π^{+} ν \bar{ν}$ and the $K_{L} \to π^{0} ν \bar{ν}$ modes, respectively.

There is a price to pay for this high theoretical cleanliness. The branching ratios are tiny—for every ten billion $K$ mesons, only one, on average, should decay into the $π ν \bar{ν}$ final state—and the experimental signature (two neutrinos in the final states) is difficult to detect because neutrinos are so weakly interacting. This is why the experimental search for these processes is a very difficult task. So far, only a few $K^{+} \to π^{+} ν \bar{ν}$ events have been observed by the E787 [3] and E949 [4] experiments at Brookhaven National Laboratory. Their combined data leads to a branching ratio that is compatible with the standard model but has a too large error to provide a very stringent test of the model. In other words, the theory is much more precise than what experimentalists are currently able to measure. The good news is that new, dedicated experimental programs aimed at substantially improving the precision of measuring these rare decays have either started or are under discussion at various laboratories: the NA62 experiment at CERN aims to collect about $50$ $K^{+} \to π^{+} ν \bar{ν}$ events/year, with a $20 %$ background, starting in 2012. On a similar time scale, the KOTO experiment at J-PARC aims to collect a few events of the neutral mode, assuming the standard model is correct. On a longer time scale, the kaon experiments related to the Project-X plan at Fermilab could be able to reach a level of precision of a few percent on both decay modes. Thanks to the high theoretical cleanliness of $K \to π ν \bar{ν}$ amplitudes, these future experiments will provide very valuable information on the flavor structure of physics beyond the standard model.

References

J. Brod, M. Gorbahn, and E. Stamou, Phys. Rev. D 83, 034030 (2011)
G. Buchalla and A. J. Buras, Nucl. Phys. B412, 106 (1994 ); A. J. Buras et al., Phys. Rev. Lett. 95, 261805 (2005); G. Isidori et al., Nucl. Phys. B718,319 (2005)
S. S. Adler et al. (E787 Collaboration), Phys. Rev. Lett. 88, 041803 (2002)
A. V. Artamonov et al. (E949 Collaboration), Phys. Rev. Lett. 101, 191802 (2008)

About the Author

Gino Isidori received his Ph.D. in physics at the University of Rome “La Sapienza” in 1996. Since 2008 he has been Research Director and head of the Theory Group at I.N.F.N. Frascati National Laboratories in Italy. He has been a CERN Fellow, professor of theoretical physics at Scuola Normale Superiore in Pisa, and held visiting positions at S.L.A.C. and the Technical University of Munich (T.U.M.). Since 2009 he has been a Fellow of the T.U.M. Institute for Advanced Study. His research interests include the formulation of theoretical models to describe flavor mixing beyond the standard model.