Irreversibility and the statistics of grain boundaries
Watching the bubbles in the head of a freshly poured beer, one sees the smaller ones disappear, and the average bubble size increase over time. Similar coarsening processes occur in many areas—the coalescence of stars into galaxies is another example. A typical feature of coarsening is that the system “forgets” its initial state, developing a statistical steady state at large times.
For most coarsening systems, we do not understand how or why the evolution produces a statistical steady state. In a paper appearing in Physical Review B, Katayun Barmak at Carnegie Mellon University and colleagues present theoretical arguments to explain the statistics of grain boundaries in a polycrystalline material after the occurrence of coarsening due to annealing [1]. Recent experimental [2] and numerical [3] work involving some of the same authors has shown that coarsening drives the statistics of grain boundaries to a Boltzmann distribution. The work of Barmak et al. offers an explanation for this behavior based on the presence of occasional irreversible changes to the grain boundary network. Their argument seems rather general and should also be relevant to other systems. From a technological standpoint, understanding coarsening in materials is important, since the physical properties of a material depend on its microstructure.
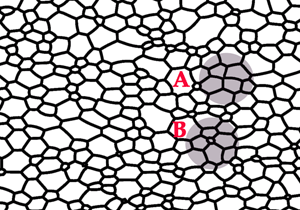
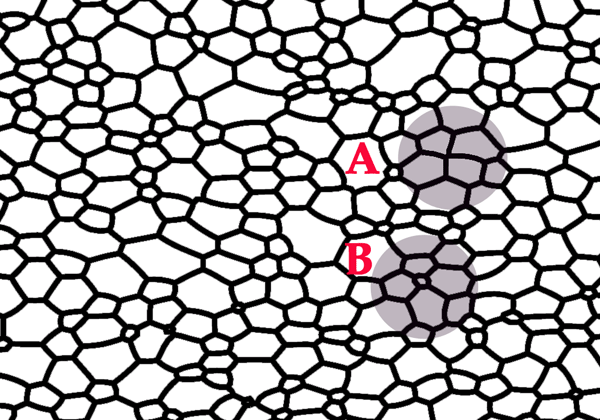
Herring and Mullins studied the local dynamics of grain boundaries (the boundaries between differently oriented crystallites of a polycrystal) over 50 years ago. Their model, sometimes known as “curvature driven growth,” amounts to steepest descent for the total surface energy, in much the same sense that a particle with velocity ·x=-∇V(x) moves by steepest descent for the potential V. To fully specify this model, one must choose the form of the surface energy. A convenient simplification, believed to be adequate for many polycrystals, is that the surface energy density of a grain boundary depends only on the degree of misorientation compared to its neighbor, vanishing in the limit of zero misorientation (when there is no grain boundary). Figure 1 shows a two-dimensional picture of the cellular network formed from such grain boundaries.
There is a large literature concerning the statistics of the polycrystals produced by the coarsening process. A recent, very attractive suggestion is that one should focus on the grain boundary character distribution (GBCD), defined as the probability that a grain boundary element has a given misorientation [2]. If this probability has density ρ, then the total surface energy at time t is
where ψ is the surface energy density as a function of misorientation, measured by angle α. Experiments suggest [2], and two-dimensional simulations confirm [3], that the GBCD produced by curvature driven growth follows a Boltzmann distribution:
Here λ is a parameter, playing the role of Boltzmann’s constant times temperature, and Zλ=∫e-ψ(α)/λdα is a normalization constant. Thus, when viewed from the perspective of the GBCD, the statistics of the grain boundaries has a steady-state character in the asymptotic limit.
In their new work, Barmak et al. address the mechanism behind this striking observation [1]. In their view, there are two essential features of the coarsening process. First, the system evolves by steepest descent of the surface energy. Second, there are singular times at which the network of grain boundaries changes irreversibly. Elaborating on the latter in the two-dimensional setting of Fig. 1: at most times the evolution is smooth, but once in a while a pair of neighboring triple points collides and the grain boundary that joins them disappears forever.
Barmak et al. suggest, by analogy with thermodynamics, that the system should evolve to minimize the free energy Fλ, obtained by adding a multiple of “entropy” to the free energy:
where λ>0 is a parameter analogous to temperature. Minimization of Eq. (3) subject to ∫ρ(α)dα=1 does indeed give the Boltzmann distribution. The entropy term is intended to capture the essential consequence of irreversibility.
The idea is attractive, but is it right? Barmak et al. address this by examining a much simpler model that still has the two essential features outlined above. In the simpler model “triple points” are represented by points on the real line, and “grain boundaries” by the intervals between the points. Each grain boundary is assigned an initial misorientation. The points move by steepest descent for the total surface energy (a system of ordinary differential equations). When two points collide, the segment between them disappears irreversibly. The associated GBCD ρ(α,t) gives the fraction of the system with misorientation α. The simplicity of the model makes simulation easy, and the numerical GBCD (observed when about 80% of the intervals have disappeared, so that coarsening is mature but finite-size effects are negligible) is again a Boltzmann distribution.
Barmak et al. also offer an evolution equation for the probability density, ρ. Noting that ρ approaches the minimum of the free energy Fλ among probability measures, they suggest that it should evolve by steepest descent for Fλ. There is a well-developed theory for what this means [4]. When the dust clears, the suggested evolution of the density obeys an equation with a simple physical interpretation involving a random walk in orientation space. Of course, this evolution has the Boltzmann distribution as its steady state.
Where does this leave us? The proposal of Barmak et al.—that the GBCD evolves by steepest descent for Fλ, eventually becoming a Boltzmann distribution because it minimizes Fλ—amounts to a sort of Landau theory, with the GBCD as its order parameter. The proposal’s success is impressive, both in the context of two-dimensional network simulations and in the context of the simpler one-dimensional model. It remains to be tested for three-dimensional polycrystals, or for grain boundary energies with anisotropy. But the key questions are more fundamental: for which coarsening systems can this method be used, and can it be given a first-principles justification? These questions are important new challenges to statistical physics.
References
- K. Barmak, E. Eggeling, M. Emelianenko, Y. Epshteyn, D. Kinderlehrer, R. Sharp, and S. Ta’asan, Phys. Rev. B 83, 134117 (2011)
- D. Kinderlehrer, I. Livshits, G. Rohrer, S. Ta’asan, and P. Yu, Mater. Sci.Forum 467, 1063 (2004)
- K. Barmak, E. Eggeling, M. Emelianenko, Y. Epshteyn, D. Kinderlehrer, and S. Ta’asan, Rendiconti di Matematica, Ser. VII, 29, 65 (2009)
- C. Villani, Topics in Optimal Transportation, Graduate Studies in Mathematics Vol 58 (American Mathematical Society, Providence, 2003)[Amazon][WorldCat]