Dynamic Heterogeneity in Amorphous Materials

The concept of dynamic heterogeneity as a key feature that characterizes disordered materials has slowly emerged from experimental studies of highly viscous molecular liquids approaching the glass transition. In these systems, relaxation spectra measured through mechanical or dielectric probes span a very broad range of relaxation times and are strongly nonexponential. This suggests the existence of wide distributions of relaxation rates.

What is the microscopic origin of these broad distributions? Looking again at the disordered structure in Fig. 1(b), it is natural to imagine that the presence of structural disorder implies that atoms in different environments move differently. The physical picture is that, at any given time, different regions in a liquid might relax in a different manner and at a different rate, thus producing broad distributions of relaxation times. However, when the system is close to the glass transition but not yet a glass, particles constantly move and rearrange, and so the distinction between different spatial environments can only hold over a finite duration.

Dynamic heterogeneity refers to the existence of transient spatial fluctuations in the local dynamical behavior. Dynamic heterogeneity is observed in virtually all disordered systems with glassy dynamics [7].

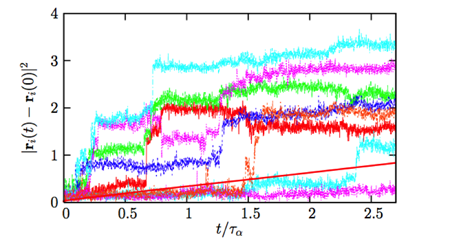
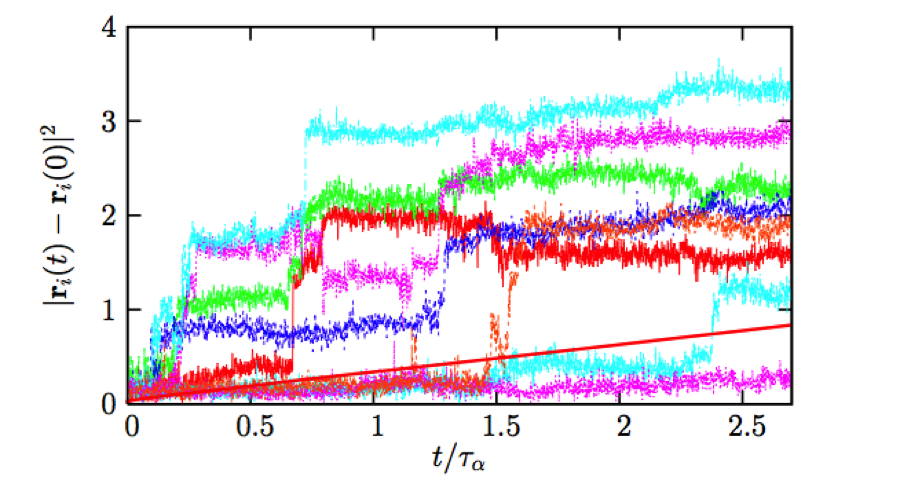
Direct confirmation of the heterogeneous character of the dynamics stems, for instance, from computer simulations of simple models of supercooled liquids (Fig. 2). Whereas the average displacement of a particle in a given time window of width $t$ is a smooth increasing function of $t$, the time signals for individual particles shown in Fig. 2 have two important characteristics.

APS/Ludovic Berthier

APS/Ludovic Berthier

×

(i) They are highly intermittent, composed of a succession of long periods of time where particles vibrate around well-defined locations that are separated by rapid “jumps.” The waiting times separating successive jumps are statistically broadly distributed.

(ii) The trajectories differ widely from one particle to another in the same system at the same time. Some particles undergo many jumps and move large distances while others are nearly immobile over the entire time window.

As with all other features related to dynamic heterogeneity, such observations cannot be made from ensemble-averaged measurements. Indeed, the characterization of dynamic heterogeneity requires the development of experimental techniques that are not only sensitive to average or typical behavior, but can also resolve the fluctuations [7,8]. For theorists, the existence of dynamic heterogeneity implies that fluctuations need to be taken into account in the description of transport properties. Therefore, materials close to a glass transition differ qualitatively from ordinary fluids, where fluctuations can typically be neglected.

The intermittency of single-particle trajectories, while clearly indicating spatiotemporal fluctuations, does not tell us how these fluctuations are correlated in space. This point was first addressed in pioneering works with four-dimensional NMR [9] and direct probing of fluctuations at the nanoscopic scale using atomic force microscopy techniques in polymeric glasses [10]. Direct visualizations of molecular trajectories are not yet possible, but recent, very elegant experimental approaches using single-molecule spectroscopy are getting close to it [11,12]. Direct visualization is possible for different types of glasses, such as colloidal [13] and granular [14,15] assemblies. All these spatially resolved measurements indicate that extended regions of space transiently behave as fast and slow regions.

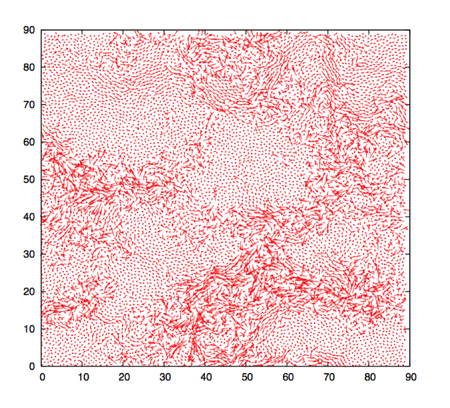
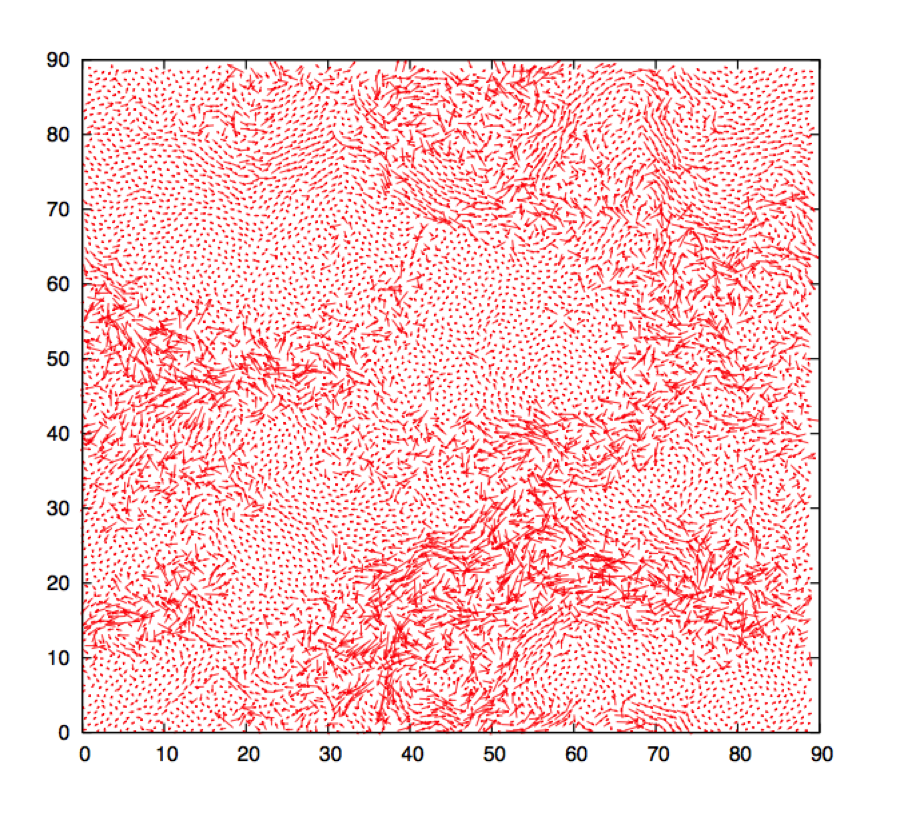
We have described dynamic heterogeneity as spatial variations in the local relaxation rate. Though hard to detect in an experiment, these fluctuations are observed in a computer simulation, where the position of each particle is known at each time step. In Fig. 3, we show an example of the visualization of spatially heterogeneous dynamics in a simple model of a supercooled liquid in two spatial dimensions. This visualization shows the existence of spatially extended “domains” where the amplitudes of single-particle displacements are correlated. These domains have no obvious counterpart in the density fluctuations [Fig. 1(b)] and only appear when dynamics is considered. However, the spatial fluctuations in Fig. 3 are reminiscent of the critical fluctuations in Fig. 1(c), with one major difference: while a thermodynamic quantity (the density) becomes critical in ordinary critical phenomena, fluctuations are only detected through dynamical quantities in highly viscous liquids.

APS/Ludovic Berthier

APS/Ludovic Berthier

×

To characterize the spatial fluctuations in Fig. 3 in a statistical manner, one must resolve the dynamics in both space and time and quantify deviations from the average behavior. To this end, one defines a “mobility,” $c_i(t,0)$, which quantifies how much particle $i$ moves between times $t=0$ and $t$ (for instance $c_i(t)=\text{exp}[-|{\mathbf{\text{r}}}_i(t)-{\mathbf{\text{r}}}_i(0){|}^2/d^2]$, with $d$ of the order of the particle size). Given two particles at separation $r$, one can measure the degree to which their mobilities are correlated. It is convenient to define a “mobility field” for a system composed of $N$ particles via

where ${\mathbf{\text{r}}}_i(t)$ is the position of particle $i$ at time $t$. The spatial correlations of the mobility are finally captured by the correlation function

which depends only on the time $t$ and the distance $r=|\mathbf{\text{r}}|$ as long as the ensemble average, denoted with brackets, is taken at equilibrium in a translationally invariant system; $G_4(r;t)$ is known as a “four-point” dynamic correlation function as it measures correlations of motion between $0$ and $t$ arising at two points, $\mathbf{\text{0}}$ and $\mathbf{\text{r}}$.

The analogy with fluctuations in critical systems becomes clear in Eq. (2) if one considers the mobility field $c(\mathbf{\text{r}};t,0)$ as playing the role of the order parameter for the transition, characterized by nontrivial fluctuations and correlations near the glass transition. This analogy is now exploited in modern theoretical treatments [2].

The above definition of a real-space correlation function of the mobility represents a vital advance in the characterization of dynamical heterogeneity. For instance, it allows the language of field theory and critical phenomena to be used in studying dynamical fluctuations in glassy systems [16,17]. Like in critical phenomena, if one assumes the existence of a single dominant length scale ${\xi }_4$, then one expects that for large distances the correlation function $G_4(r;t)$ decays as

where $p$ is a critical exponent. It is also natural to define the susceptibility associated with the correlation function

If the prefactor $A(t)$ in Eq. (3) is known, the susceptibility ${\chi }_4(t)$ can be used to infer the typical number of particles involved in the correlated motion shown in Fig. 3. That is, ${\chi }_4(t)$ may be interpreted as the “volume” of the correlated clusters.

Further, ${\chi }_4(t)$ can also be obtained from the fluctuations of the total mobility $C(t,0)=\int d^d\mathbf{\text{r}}c(\mathbf{\text{r}};t,0)$, through

In practice, this formula permits an efficient measure of the degree of dynamical heterogeneity, at least in computer simulations and in those experiments where the dynamics can be spatially and temporally resolved. As long as $c(\mathbf{\text{r}};t,0)$ appropriately quantifies atomic motion, ${\chi }_4(t)$ can be measured in a variety of systems, serving as a basis for comparing the extent of dynamical heterogeneity, and has become a central tool in characterizing dynamic heterogeneity in amorphous materials [7].

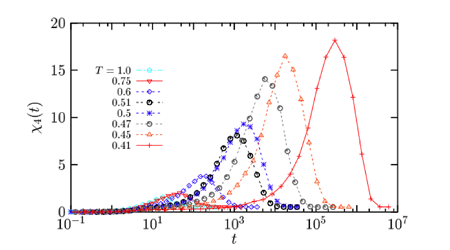
The dynamical function ${\chi }_4(t)$ has now been measured in computer simulations of many different glass-forming liquids, by molecular dynamics, Brownian, and Monte Carlo simulations [18–23]. An example is shown in Fig. 4 for a Lennard-Jones numerical model, but the qualitative behavior is similar in all cases [24–26]: as a function of time, ${\chi }_4(t)$ increases at first, it has a peak on a timescale of the order of the typical relaxation time of the fluid, and then it decreases at large times. This time dependence simply reflects the transient nature of the dynamical heterogeneity.

APS/Ludovic Berthier

APS/Ludovic Berthier

×

The peak value of ${\chi }_4(t)$ approximately measures the volume over which structural relaxation processes are correlated. Therefore the most important result obtained from data such as those presented in Fig. 4 is the temperature evolution of the peak height, which is found to increase when the temperature decreases and the global dynamics slows down. Such data provide evidence that the approach to the glass transition is accompanied by increasingly long-ranged spatial correlations of the dynamics.

In experiments, direct measurements of ${\chi }_4(t)$ have been made in colloidal [27] and granular materials [14,15] close to the colloidal and granular glass transitions, and also in foams [28] and gels [29], because dynamics is more easily spatially and temporally resolved in those cases. The results obtained in all these cases are again broadly similar to those shown in Fig. 4, both for the time dependence of ${\chi }_4(t)$ and its evolution with a change of the relevant variable controlling the dynamics.

Obtaining information on the behavior of ${\chi }_4(t)$ and $G_4(r;t)$ from experiments on molecular systems is difficult, because it is hard to disentangle the spontaneous fluctuations embodied in ${\chi }_4(t)$ in Eq. (5) from the experimental noise. Such measurements are, however, crucial because numerical simulations and experiments on colloidal and granular systems can typically only be performed for relaxation times spanning at most $5$– $6$ decades. On the other hand, in molecular liquids, up to $14$ decades are, in principle, relevant, and extrapolation of simulation data all the way to the experimental glass transition is fraught with difficulty. Indirect estimates of ${\chi }_4(t)$ from experiments are discussed below.

We mentioned above that a growing peak in ${\chi }_4(t)$ “directly” reveals the growth of a dynamic correlation length scale as the glass transition is approached. This can only be true if the assumptions made in Eq. (3) for the scaling form of $G_4(r;t)$ are correct. Dynamic length scales should, in principle, be obtained by direct measurements of a spatial correlation function.

However, in contrast to ${\chi }_4(t)$, detailed measurements of $G_4(r;t)$ are technically more challenging as dynamic correlations must be resolved in space over a large range of distances with a very high precision, and so there is much less data to draw on. From the point of view of numerical simulations where many measurements of ${\chi }_4(t)$ were reported, the main limitation to properly measuring ${\xi }_4$ is the system size. This might seem surprising, as typical numbers extracted for the correlation length scale ${\xi }_4$ are rather modest, but a precise determination of ${\xi }_4$ requires an accurate study of the tail of $G_4(r;t)$ at large $r$, which entails considerable numerical effort [30,31].

Such studies are important as they allow the dynamical length scale ${\xi }_4(t)$ to be measured directly. Moreover, such studies help infer the behavior of ${\xi }_4(t)$ from measurements of ${\chi }_4(t)$. Published work is consistent with ${\chi }_4(t)/G_4(0,t)$ representing the number of particles involved in heterogeneous relaxation. Therefore, truly “direct” measurements indeed confirm that the increase of the peak of ${\chi }_4(t)$ corresponds, as expected, to a growing dynamic length scale ${\xi }_4(t)$ [21,23,26,30,31].

Instead of direct inspection of $G_4(r;t)$, it is often convenient to analyze its Fourier transform,

which is known as the four-point structure factor of dynamic heterogeneity. In Fourier space, the large domains observed in Fig. 3 affect the low wave vector behavior of $S_4(q;t)$ in the form of a peak that grows when the glass transition is approached. This peak is often fitted with the Ornstein-Zernike functional form that is frequently used in conventional critical phenomena [3].

Although readily accessible in numerical simulations, the fluctuations that give access to ${\chi }_4(t)$ are, in general, very small and impossible to measure directly in experiments, except when the range of the dynamic correlation is macroscopic, as in granular materials [14] or in soft glassy materials where it can reach the micrometer and even millimeter range [28,29,32]. To access ${\chi }_4(t)$ in molecular liquids, one should perform time-resolved dynamic measurements that probe very small volumes, with a linear size of the order of a few nanometers.

Fortunately, simpler alternative procedures exist. The central idea underpinning these solutions is the realization that if it is generally hard to detect noise in an experiment, it is usually simpler to measure the response of a system to an external perturbation. In the linear response regime, both types of measurements can often be related to one another by fluctuation-dissipation theorems [3]. The physical motivation is that while four-point correlations offer a direct probe of the dynamic heterogeneities, other multipoint correlation functions might also give useful information about the microscopic mechanisms leading to these heterogeneities.

For example, one might expect that a local fluctuation of the enthalpy $\delta h_x(t=0)$ at position $x$ and time $t=0$ triggers or eases the dynamics in its surroundings, leading to a systematic correlation between $\delta h_x(t=0)$ and $c(x+r;t,0)$. A similar effect is expected for a local fluctuation of the density. These physical intuitions suggest the definition of a family of three-point correlation functions that relate thermodynamic fluctuations at one point to dynamical ones at another. Crucially, some of these three-point correlations are both experimentally accessible and give bounds or approximations to the four-point dynamic correlations [33].

Based on this insight, one may obtain a lower bound on ${\chi }_4(t)$ by using a fluctuation-dissipation relation, which is valid at equilibrium when the energy is conserved by the dynamics [33]:

where ${\chi }_T(t)$ quantifies the response of the average mobility to an infinitesimal change in the temperature $T$, and $c_P$ is the specific heat per particle. The response ${\chi }_T(t)$ can be experimentally accessed by measuring the average of a dynamical correlator, $⟨C(t,0){⟩}_T$, at nearby temperatures, $T$ and $T+\delta T$, in the linear regime $\delta T\ll T$:

The main experimental advantage of Eq. (8) is that spatiotemporal resolution is not needed, contrary to Eq. (5).

Detailed numerical simulations and theoretical arguments [26] strongly suggest that the right-hand side of Eq. (7) actually provides a good estimate of ${\chi }_4(t)$ in supercooled liquids, and not just a lower bound. Similar estimates exist considering density instead of the temperature in Eq. (8). These are useful when considering colloidal or granular materials where the glass transition is mostly controlled by the packing fraction. The quality of the corresponding lower bound was tested experimentally on granular packings close to the jamming transition [34], and numerically for colloidal hard spheres [30,35].

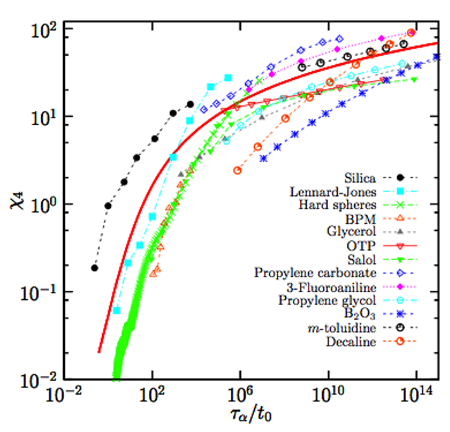
We show in Fig. 5 a compilation of data [36] for the evolution of the peak height of ${\chi }_4$, in a representation inspired by the theory of dynamic critical phenomena [3]. These data represent an experimental confirmation that dynamic fluctuations and correlation length scales grow appreciably when molecular liquids approach the glass transition. However, we also learn that typical length scales do not become very large (remaining in the nanometer scale for molecular glass formers) before liquids vitrify in a nonergodic state, and that an “ideal” glass critical point is not readily accessible to experiments.

APS/Ludovic Berthier

APS/Ludovic Berthier

×

The above results are also relevant as many theories of the glass transition have assumed or predicted that the dynamics slows down because there are increasingly large regions over which particles have to relax in a correlated manner [1]. However, in the absence of experimental signs of growing length scales, these theoretical constructions have remained speculative.

The measurements of the spatial extent of dynamic heterogeneity, in particular ${\chi }_4(t)$ and $G_4(r;t)$, seem to provide the long-sought evidence that the glass transition must be considered as a form of critical or collective phenomenon involving growing timescales and length scales. This is important for the field of glass transition, even though a conclusive understanding of the relationship between dynamical length scales and relaxation timescales remains the focus of intense research [2].

From a theoretical perspective, we are familiar with the idea, borrowed from equilibrium critical phenomena [3], that when correlation length scales get large, microscopic features of the system become unimportant and “universal” behaviors emerge. Whether realistic glassy systems have length scales that are large enough for such a universal description remains unclear. Although most theoretical approaches are in this spirit, one should perform an equally careful treatment of pre-asymptotic effects, which obviously matter for experiments that are performed far away from (putative) criticality. Therefore, theories of the glass transition are still crude descriptions of reality, despite large research efforts.

Distinct microscopic mechanisms have been proposed that all give rise to growing dynamic correlations similar to the ones revealed by four-point functions. This relative abundance of approaches can be interpreted in two ways. A first view is to consider dynamic heterogeneity as a unifying physical phenomenon that accompanies the formation of glasses, and is central to its theoretical understanding. The second, more pessimistic interpretation is that if any reasonable theory predicts increasingly spatially heterogeneous dynamics, then studying dynamic heterogeneity might not help make substantial theoretical progress. This argument is balanced by the fact that the mere observation of dynamic heterogeneity has forced theorists to work hard on many fronts to understand what sort of microscopic mechanism is able (or not) to provide, for instance, new insights or quantitative predictions for the behavior of multipoint correlation functions, susceptibilities, and dynamic correlation length scales [7].

Several theoretical schemes, such as mode-coupling theory [37], random first-order transition theory [38], dynamic facilitation approach [39], and frustration-limited domain scaling picture [40], have now been developed to the point that they provide useful guides to understand and analyze various aspects of dynamic heterogeneity (see Ref. [2] for a general theoretical review). One hopes that these approaches contain useful seeds for the construction of a “unified” theory of the glassy state. In all of these approaches, dynamic heterogeneity and spatiotemporal fluctuations feature as central concepts.

Although we mostly discussed supercooled liquids near the molecular glass transition, other materials too have played an important role in the development of the concepts and tools described above. Several soft condensed materials, such as colloidal assemblies, have been instrumental in our understanding of the phenomenon of dynamic heterogeneity because they are similar to molecular liquids but with constituents that are so much larger than atoms (in the $50\text{nm}$– $1\mu \text{m}$ range) that they can be more easily visualized [13,27]. Driven granular media (sheared or agitated systems) also undergo a “granular” glass transition that is empirically similar to the molecular transition. In that case, grains can be directly tracked using a standard camera [14,15].

In the introduction we alluded to the rigidity transition occurring in athermal disordered granular packings. This “jamming” transition arises in an assembly of rigid particles when the system cannot be compressed anymore, and is thus mainly a geometric transition where thermal fluctuations play no role. For spherical particles of equal sizes, this transition occurs near “random close packing” ${\phi }_{\text{rcp}}\approx 0.64$ [5]. The jamming transition is relevant also for athermal assemblies of soft particles, such as foams and emulsions, which are additional examples of disordered rigid materials [4]. Connections with the physics of glasses are still rather speculative but are currently the focus of an important research effort. Detailed studies of dynamic heterogeneity in packings of soft and hard particles near random close packing started to appear only recently [41–44], and could help elucidate similarities and differences between glasses and granular materials.

One of the most frequently asked questions in studies of dynamical heterogeneity is whether the observed dynamic fluctuations and correlations might have a structural origin: Is there, after all, a “hidden” thermodynamic order parameter that would exhibit spatial fluctuations comparable to the ones revealed by dynamic heterogeneity studies? This question has attracted sustained interest. For example, in very early numerical work on dynamic heterogeneity, immobile regions were discussed in connection with compositional fluctuations in fluid mixtures [45]. However, dynamic heterogeneity would not have emerged as an important concept if a simple, direct connection between structural order and relaxation dynamics had been satisfactorily established in amorphous materials. In that case, research would be dedicated to understanding the development of structural correlations at low temperatures in supercooled liquids, and to developing tools to measure, quantify, and analyze such static features.

Having said that, recent research on isoconfigurational ensembles [46], amorphous order [47], and point-to-set correlations [48] suggests that the structure of disordered materials might be the next topic where new discoveries and concepts emerge. While two-point static correlations are poorly correlated to the evolution of the glassy dynamics, there is plenty of room to invent more complicated correlation functions that would more accurately characterize the local structure of complex disordered media and explain their fascinating physical properties.