Quantum dots shine unsteadily
Artificial atoms are a cornerstone of emerging technologies that promise to make practical use of the laws of quantum mechanics. In principle, artificial atoms should behave like real atoms but be compatible with a solid-state environment. As such, they could serve as solid-state quantum bits (qubits) ideally suited to interfacing with photonic qubits. They could store, manipulate, and retrieve quantum information, or could generate single photons or entangled photon pairs for use in photonic quantum circuits. Artificial atoms come in many forms, such as single molecules embedded in a host matrix, color centers in diamond, dopant ions in crystalline lattices, and various types of quantum dot.
Quantum dots are zero-dimensional semiconductor structures whose optical and electronic properties can be engineered. In particular, their size and shape determine the energies of their internal quantum states and of the photons they emit and absorb. Another advantage of quantum dots is that they can be charged. The fundamental excitations of a neutral quantum dot are bound electron-hole states known as excitons. If a single excess charge is introduced into a quantum dot, photoexcitation results in a trion state, which consists of an exciton with an additional electron or hole. This system has tremendous potential for quantum technologies, as the spin of the trion’s excess charge can be coherently manipulated, making it an effective qubit [1]. In addition, the qubit exists in the ground state, which can allow for extremely long coherence times, of the order of seconds in some systems.
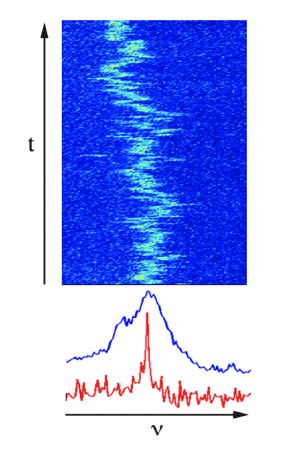
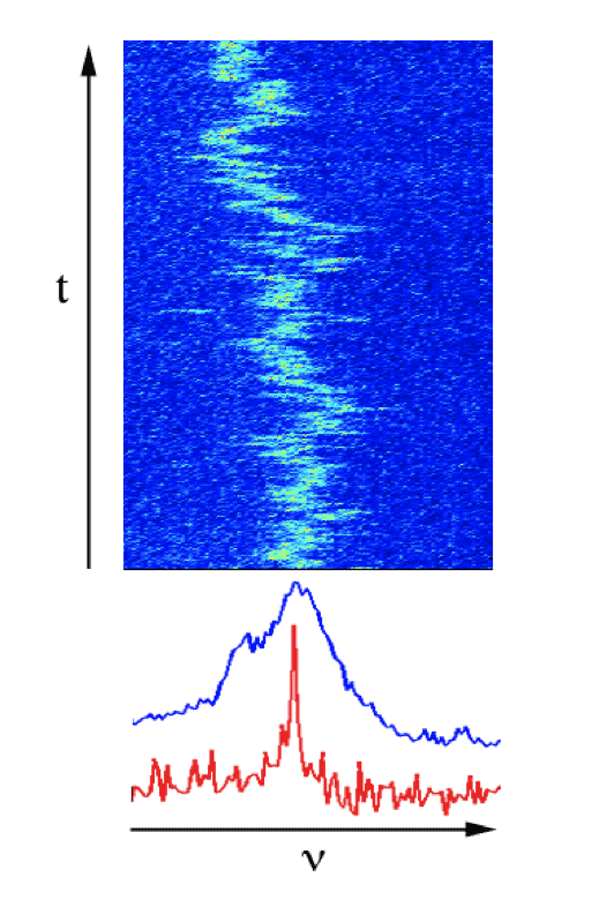
A major obstacle to practical applications of quantum dots and other solid-state artificial atoms, however, is their interaction with their local environment. Such interactions can completely disrupt the quantum state of the artificial atom, or, if the interactions operate on a longer timescale, can cause random fluctuations of the energy of the quantum state. For example, photons generated by single artificial atoms tend to wander erratically in frequency, a phenomenon known as spectral diffusion (see Fig. 1). Spectral diffusion afflicts many types of solid-state artificial atoms—single molecules embedded in solid host matrices [2], the nitrogen-vacancy (NV) color center in diamond [3], and single quantum dots [4]—although in some systems it can be reduced by careful engineering [1,3,5].
Writing in Physical Review B, Gregory Sallen of Joseph Fourier University in Grenoble, France, and his colleagues report novel photon correlation measurements, on a subnanosecond timescale, of the trion state observed in a quantum dot embedded within a nanowire [6]. This type of quantum dot is of great interest because of the way it is made: Epitaxial growth of nanowires is interrupted by the growth of layers to form quantum dots within the nanowires. This process potentially provides good photophysical robustness. In addition, facile manipulation of the nanowire allows compatibility with a wide range of hosts and environments. The trion lifetime of picoseconds means that the minimum possible emission linewidth should be approximately micro-electron-volt, but the observed linewidth is over three orders of magnitude broader at milli-electron-volts. Sallen et al. use their newly developed photon correlation technique [7] to show that the main cause of line broadening is rapid spectral diffusion with a characteristic timescale of nanoseconds. No other published techniques can detect inhomogeneous broadening at this timescale.
In order to gain more insight into the spectral diffusion process, Sallen et al. study the dependence of the spectral linewidth of the trion transition and show that it is saturated, i.e., independent of pump power. Considering these results, the authors propose a model by which spectral diffusion results from repeated ejection and recapture of a single charge by the quantum dot.
However, many other models can be constructed that display similar saturation behavior. For example, if we imagine spectral diffusion following a random walk among a finite number of environmental charge configurations, then saturation occurs on timescales long enough that all charge configurations have been sampled [3]. Interestingly, Sallen et al. find that a single well-defined timescale characterizes the spectral diffusion process, a result that stands in contrast to the more complex spectral diffusion, with distinct fast and slow timescales, found in colloidal quantum dots [8,9]. A single well-defined rate implies a relatively simple or uniform local environment. Sallen et al. do not extend their correlation technique to longer timescales, although this could be done in principle [2] and would provide further insight into the system.
The charge dynamics proposed by Sallen et al. for the nanowire material make the trion useless as a qubit, since rapid charge ejection and recapture would rapidly remove any stored quantum information. This can be seen from a spectrum obtained by the authors from a single quantum dot that shows the simultaneous detection of a neutral exciton, a charged exciton, and a neutral biexciton. As the trion cannot coexist with these other states, it must be repeatedly gaining and losing its excess charge during the acquisition time of the measurement. It is this charge-discharge cycle, according to Sallen et al., that is responsible for the rapid spectral diffusion, amounting to a qubit dephasing timescale of nanoseconds—too fast for any practical application that requires qubits to exist for long enough to be manipulated. The rather dire implications of this charge-discharge dynamics hypothesis really should be tested further, as spectral diffusion may be caused by other environmental charge fluctuations, driven by phonons or other mechanisms, that are less detrimental to spin qubits.
The problem of spectral diffusion must be solved if this solid-state artificial atom is to be of use in quantum technologies. Its rapid timescale and large milli-electron-volt frequency range stand in stark contrast to spectral diffusion in some other quantum dot sources, which may be slow, occurring on a second timescale [10], or, for certain self-assembled quantum dots, negligible [1]. The spectral diffusion properties reported for the quantum dots may stem from the way they are made, in which nanowire growth is interrupted by growth of the lower-band-gap semiconductor, which then forms a quantum dot in the nanowire. It seems that, in contrast with self-assembled quantum dots where the semiconductor surface can be far from the quantum dot, these quantum dots could have a strong interaction with the surface of the nanowire. If this is the case, the passivation (removal) of surface states may be critical in this material.
Sallen et al. have revealed some essential parameters of the spectral diffusion that plagues their system. The next step in developing this material would be to look at means for mitigating the spectral diffusion. One possibility might be to further engineer the material so that the trion state is stable and does not rapidly oscillate between the neutral and charged state. Another possibility might be to look for ways to reduce and ultimately eliminate the spectral diffusion in these materials.
References
- D. Press, T. Ladd, B. Zhang, and Y. Yamamoto, Nature 456, 218 (2008)
- A. Zumbusch, L. Fleury, R. Brown, J. Bernard, and M. Orrit, Phys. Rev. Lett. 70, 3584 (1993)
- Y. Shen, T. Sweeney, and H. Wang, Phys. Rev. B 77, 033201 (2008)
- S. Empedocles and M. Bawendi, J. Phys. Chem. B 103, 1826 (1999)
- A. Walser, A. Renn, S. Gotzinger, and V. Sandoghdar, Chem. Phys. Lett. 472, 44 (2009)
- G. Sallen, A. Tribu, T. Aichele, R. André, L. Besombes, C. Bougerol, M. Richard, S. Tatarenko, K. Kheng, and J-P. Poizat, Phys. Rev. B 84, 041405 (2011)
- G. Sallen et al., Nature Photon. 4, 696 (2010)
- L. Coolen, X. Brokmann, P. Spinicelli, and J.-P. Hermier, Phys. Rev. Lett. 100, 027403 (2008)
- T. Plakhotnik et al., Phys. Rev. Lett. 105, 167402 (2010)
- M. Fernée et al., Phys. Rev. B 81, 155307 (2010)