Few and Far Between

Sitabhra Sinha

Viewpoint

Few and Far Between

Sitabhra Sinha

The Institute of Mathematical Sciences C.I.T. Campus, Taramani, Chennai 600113, India

October 17, 2011• Physics 4, 81

How nodes connect to each other may explain why we don’t see certain classes of networks.

Figure caption — **Figure 1:** Social network of the characters appearing in the movie *Love Actually* (2003), with node size proportional to the total dialogue (a measure of screen time) assigned to a particular character. Links connect pairs of characters present in the same scene. The node at the top left corresponding to the character of David (the prime minister, played by Hugh Grant), which is one of the hubs of the network, has a much larger number of connections than the average degree for the network. The work of Del Genio *et al.* suggests that it is not possible for the number of such hubs to become comparable to the total number of nodes as a scale-free network grows to arbitrarily large sizes.

At the end of the 20th century, the study of networks—systems of nodes connected by links—took off as scientists realized how ubiquitous they were. Complex networks describe interactions among proteins in a cell, coordinate communication among the neurons in our brain, and govern how individuals in a society connect. The list goes on. Many fundamental questions about networks remain unanswered, however, including several on scale-free networks, which are characterized by a power-law distribution in the number of connections (degree) each node has.

Now, in a paper in Physical Review Letters, Charo Del Genio at the Max Planck Institute for the Physics of Complex Systems, Germany, and coauthors tell us that the only kind of scale-free network that is possible is one with an average degree that remains finite as its size becomes arbitrarily large [1]. The connection density $C$ of a network can be interpreted as the ratio of the average degree to the network size (the number of nodes, $N$ ), and so this result implies that all realizable scale-free networks are sparse ( $C \to 0$ as $N \to \infty$ ). The paper should stimulate fresh activity in this area, as it appears to contradict earlier mathematical results [2] which suggested that growth by node and link duplication would give rise to dense scale-free networks.

Scale-free networks [3] have become prominent recently, but power-law degree distributions have been known for some time. In the 1960s, the polymath Derek de Solla Price proposed [4] a preferential attachment scheme—now colloquially referred to as the “rich get richer” effect, first studied by George Yule—that generates power-law distributions seen in many contexts, including several in economics, such as the Pareto law for income distribution [5]. For networks, preferential attachment works as follows [6]: Start with a existing network and at subsequent time steps add new nodes that connect to existing ones preferentially, according to their degree. If the probability that a new node will connect to a node of degree $k$ is proportional to $k$ , then it can be shown that in the steady state the network exhibits a power-law degree distribution $P (k) \sim k^{- γ}$ , where the exponent $γ = 3$ . As many networks (the internet is one example) that evolve by accumulating nodes show scale-free degree distribution, one expects the evolutionary algorithm above to describe their growth. However, scale-free networks that are prevalent, whose exponents can span a variety of values, appear to mostly cluster around $γ = 2$ , not $3$ .

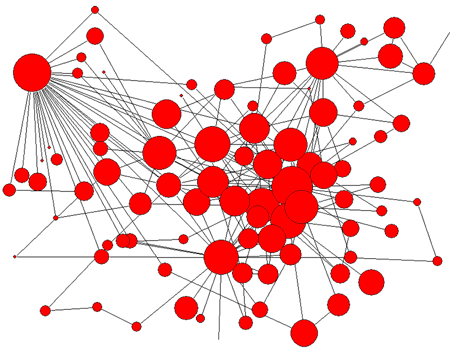
Why does the value of the exponent matter? For one thing, it governs the statistics of the various moments of the distribution of the degree (including the average degree and its standard deviation). This has repercussions for the dynamical processes on the networks. An example is how a contagion spreads in a population where the contact network among individuals is scale-free. The epidemic can only spread if the rate of infection exceeds a threshold, which is the ratio of the first and second moments of the degree distribution. If the distribution is a power law with an exponent between $2$ and $3$ , the second moment diverges so that this ratio is zero and the threshold disappears. In other words, even an infection with an arbitrarily small rate of spread can result in an epidemic that spans the entire population [7]. This may appear to have ominous consequences, but there is a silver lining. A sparse scale-free network is characterized by the existence of hubs—nodes with a very high degree compared to the average (Fig. 1)—that dominate the spreading process. Therefore, identifying and selectively immunizing the few “super-spreaders” would be a workable control strategy.

However, when the exponent is smaller than $2$ , the first moment diverges with system size. This means that the number of hubs is no longer small but rather of the order of the size of the network. Selective control of such a large number of hubs is no longer an efficient strategy. Fortunately, with a few key exceptions, most social networks do not appear to be scale-free: diseases that spread through casual social interaction may have a finite threshold.

So, can there be scale-free networks that exhibit power-law nature at arbitrarily high degrees and still have $γ < 2$ ? The few empirical reports of such systems have not decisively settled the issue. They were mostly based on small data sets, with possibly unreliable statistics [8]. However, a mathematical result on scale-free networks that are grown by adding nodes that duplicate the links of a randomly selected existing node with a selection probability $p$ suggests that degree distribution exponents between $1$ and $2$ can be obtained for $p > 0.5$ [2]. And there the matter seemed to rest. In their paper, however, Del Genio et al. claim that such networks can be ruled out purely on theoretical grounds. Although their proof does not depend on the exact procedure used to construct a network from its degree sequence, i.e., the complete list of the number of connections that each of its nodes has, it is instructive to consider one. For example, the Havel-Hakimi algorithm [9] begins with a graph with no links and then gradually constructs links consistent with a given degree sequence, arranged in a non-increasing order. The first node is connected to the next vertices in this list, and then removed from the list. The list is rearranged and the process is repeated until all the degrees are properly assigned and (a) either the network is constructed successfully, or (b) the conditions cannot be fulfilled at some stage, so that the corresponding network cannot be constructed. Using analytical reasoning as well as numerical calculations, the authors show that no degree sequences corresponding to scale-free networks having exponents between $0$ and $2$ can be realized.

An important question the work raises is what it implies for earlier mathematical results on dense scale-free networks obtained by duplication processes. Could it be that realizable instances of such networks may exist in principle but are so rare that they will never be encountered in practice? Further research will hopefully clarify this issue. It is important to note that the new result does not imply that all networks have to be sparse. Indeed, dense networks where each node is connected to all others are easy to realize. Similarly, as the authors point out, degree distribution exponents smaller than $0$ correspond to dense networks. However, such networks are not the familiar scale-free networks. Thus, for real scale-free networks, the number of hubs will always be much smaller relative to the size of the network. This is not necessarily good news. While the sparse nature of the network will make it possible to formulate efficient immunization strategies based on identification of hubs, it also suggests that targeted attacks on a few vulnerable nodes in large complex technological systems, such as the internet, can bring them down. Recent results also show that sparse inhomogeneous networks are the most difficult systems to control by driving a small fraction of their nodes with input signals [10].

References

C. I. Del Genio, T. Gross, and K. E. Bassler, Phys. Rev. Lett. 107, 178701 (2011)
F. Chung and L. Lu, Complex Graphs and Networks (American Mathematical Society, Providence, 2006)[Amazon][WorldCat]
G. Caldarelli, Scale-Free Networks (Oxford University Press, Oxford, 2007)[Amazon][WorldCat]
D. J. de Solla Price, Science 149, 510 (1965)
S. Sinha, A. Chatterjee, A. Chakraborti, and B. K. Chakrabarti, Econophysics: An Introduction (Wiley-VCH, Weinheim, 2011)[Amazon][WorldCat]
R. Albert and A.-L. Barabasi, Science 286, 509 (1999)
R. Pastor-Satorras and A. Vespignani, Phys. Rev. Lett. 86, 3200 (2001)
A. Clauset, C. R. Shalizi, and M. E. J. Newman, SIAM Review 51, 661 (2009)
S. L. Hakimi, SIAM J. Appl. Math. 10, 496 (1962)
Y.-Y. Liu, J.-J. Slotine, and A.-L. Barabasi, Nature 473, 167 (2011)

About the Author

Sitabhra Sinha is a professor of theoretical physics and the dean of the Computational Biology Graduate Program at the Institute of Mathematical Sciences (IMSc) in India. He did his Ph.D. at the Indian Statistical Institute, Kolkata, and postdoctoral research at the Indian Institute of Science, Bangalore, and at the Weill Medical College of Cornell University, New York, joining the faculty of IMSc in 2002. His research falls broadly under complex systems, nonlinear dynamics, and statistical physics, with applications to systems biology, economic and social sciences, and computational linguistics.