Taming Nonequilibrium Statistics

Andrea Parmeggiani

Viewpoint

Taming Nonequilibrium Statistics

Laboratoire Charles Coulomb, CNRS UMR 5221, Université Montpellier 2, Montpellier, France
Laboratoire de Dynamique des Interactions Membranaires Normales et Pathologiques, CNRS UMR 5235, Université Montpellier 2/Université Montpellier 1, Montpellier, France

October 22, 2012• Physics 5, 118

Few mathematical tools exist for describing non-equilibrium systems, but new methods may emerge from the study of a simple transport model.

Figure caption — **Figure 1:** The asymmetric simple exclusion process is a toy model for describing nonequilibrium behavior. (Top) The model in the abstract. In an infinitesimal time window, a particle located on any one site hops to a site to its right with rate $p$ , and to its left with rate $q$ , provided these sites are empty. The lattice can exchange particles with the outside world, with particles entering or leaving the left end of the chain with rates $α$ and $γ$ , respectively, and entering and leaving the right side of the chain with rates $δ$ and $β$ , respectively. (Bottom) The model can be used to study protein “traffic” along a filament. In the case shown here, $q$ , $γ$ and $δ$ are equal to zero.

Imagine a tall column of gas that has been resting on a table for several days, at a fixed temperature and isolated from any exchange of particles or heat with the outside world. A fact familiar to students learning the statistical properties of an ideal gas in a gravitational field is that the density of the gas falls off exponentially from the bottom of the column to the top.

In the real world though, equilibrium states like the column of gas are more the exception than the rule. Systems do interact with their environment and some of the most interesting ones are time-dependent (transient), like the current following a capacitor discharge, or in a steady state, like the current in a battery-driven circuit. Yet all the tools of statistical physics that allow us to start with a microscopic picture and calculate macroscopic and thermodynamic quantities, such as the density distribution of particles, entropy, or free energy, assume the system being described is in equilibrium. Nonequilibrium systems can be studied numerically, but despite decades of research, it is still very difficult to define the analytical functions from which to compute their statistics and have an intuition for how these systems behave.

In Physical Review Letters, Mieke Gorissen at Hasselt University, Belgium, and colleagues report an important contribution to building a statistical theory for nonequilibrium systems [1]. They have analytically derived the functions that describe (exactly) the steady-state transport of particles and its statistical fluctuations for the most general form of the so-called asymmetric simple exclusion process (ASEP) [2], a widely used one-dimensional toy model that has been applied to the study of traffic and molecular transport. Their results provide a framework for relating microscopic descriptions of nonequilibrium systems to macroscopic approaches, such as the so-called “fluctuation theorems” [3].

Nonequilibrium systems are usually characterized by the presence of a current, which is associated with the motion of particles or energy carriers. However, even when these systems evolve to a steady state, their dynamics can be complex, with anomalous properties and statistical fluctuations dominating the average behaviors. For example, we still have to build a microscopic theory for how heat diffuses in a nanoscopic wire, such as a carbon nanotube placed between two thermal reservoirs at different temperatures: the Fourier’s law that describes heat transfer in a normal wire fails at the nanoscale.

To calculate the statistics of an equilibrium system, we use the Boltzmann-Gibbs formulation, which counts each available state and its energy, $ε$ , and gives it a statistical weight proportional to $exp (- ε / k_{B} T)$ . If a similar way to count states existed for nonequilibrium systems, we would be able to compute quantities like the free energy, predict different thermodynamic phases of nonequilibrium matter, or understand how systems respond to perturbations (with local or collective and long-range fluctuations). From a purely fundamental perspective, it is interesting to ask if a universal formalism can even exist for nonequilibrium systems.

One approach to finding such a formalism from microscopic laws is to study simple models that capture the essence of a nonequilibrium system, but are still mathematically tractable. A favorite type of model is the “driven lattice gas,” where an external field biases the motion of particles along a lattice, or the particles themselves exploit some source of energy to move. These models have been applied to the study of pedestrian and car traffic [4,5] and motor protein transport [5]. They can also describe the dynamics of granular and glassy materials.

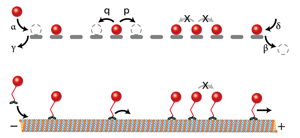
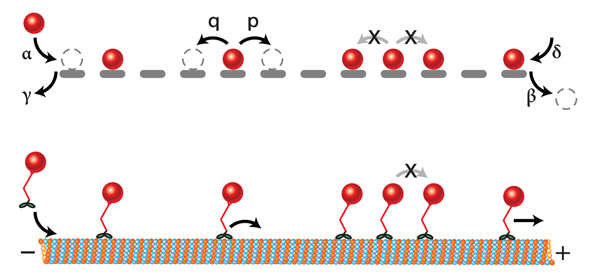
Among driven lattice gas models, the asymmetric simple exclusion process (ASEP) [2] is considered the most instructive prototype because of its simplicity. (Historically, the model was developed to describe the ribosomal activity along messenger RNA that leads to the synthesis of proteins.) The ASEP assumes that particles move along a discrete chain of length $L$ (Fig.1), and that each particle can hop to the left or the right (not necessarily at equal rates), only provided these sites are empty. If this lattice is “open,” it can exchange particles with an infinite reservoir of particles on either end of the chain.

What makes it mathematically challenging to study an ASEP is that the average occupancy of particles on the ith site, $〈 n_{i} 〉$ , depends on higher correlation functions like $〈 n_{i} n_{i + 1} 〉$ that in turn depend on $〈 n_{i} n_{i + 1} n_{i + 2} 〉$ and so on. One ends up with an infinite hierarchy of nonlinear equations that are very difficult to solve exactly.

Advanced mathematical methods or model-specific approximations are therefore necessary to get a solution either of the so-called “master equation,” which describes the time evolution of the probability distribution of one microscopic configuration via all possible transitions between the $2^{L}$ configurations of the system, or to build a “generating function” which allows all the correlation functions (statistical moments and cumulants) of the stochastic process to be computed. So far, researchers have been able to solve, exactly, for the average steady-state density and current [6,7], but for the last few decades, they have been searching for the analytical functions that give the full statistics of the current. These statistics, or cumulants, describe the standard deviation of the current fluctuations, their asymmetry, and so on. Knowing them is practically equivalent to knowing all possible states of the system and their corresponding statistical weight.

In a mathematical tour de force, Gorissen et al. have overcome this hurdle. They present an elegant solution for building and computing the cumulant generating function of the current fluctuations in the stationary state for any system size $L$ with open boundary conditions. In other words they invented a method to count exactly all possible statistical fluctuations of the current in the steady state. To do this, the authors generalized a powerful method called the “matrix product ansatz” (which resembles the matrix operators that act on bra and ket states in quantum mechanics) [6,7] and relate their results to the large deviation functional of the current and its cumulant generating function. These functionals, emerging from probability theory [3,8], are serious candidates for generalizing the Boltzmann-Gibbs formalism to nonequilibrium systems and show that the current can be used as a sort of free energy in nonequilibrium systems.

It may seem that an analytical solution is simply a satisfying way to tell us that our numerical calculations are working, but in fact, it will be a useful intuitive guide on complex problems, such as time dependent behaviors. Other existing challenges in this respect are describing nonequilibrium systems in contact with finite particle reservoirs [9] or understanding ASEP-like dynamics in complex networks [10].

Gorissen et al.’s work may also help estimate the finite size effects that come into play in real applications and devices. In biological systems, molecular machines work under very different conditions with respect to our meter-sized world. Similarly, in the era of miniaturized electronics, we must find ways to optimize heat dissipation in nanoelectronic circuits. These systems experience strong statistical fluctuations because they are small, and their behavior is highly sensitive to changes in the surrounding medium. Understanding the thermodynamics of small systems in nonequilibrium conditions remains a major challenge.

The work of Gorissen et al. and other researchers are ushering us into a new perspective of nonequilibrium phenomena, where we can compare statistical theories with real experiments at any spatiotemporal scale, explore new concepts, and conceive useful devices from dynamic nonequilibrium world.

References

M. Gorissen, A. Lazarescu, K. Mallick, and C. Vanderzande, “Exact Current Statistics of the Asymmetric Simple Exclusion Process with Open Boundaries,” Phys. Rev. Lett. 109, 170601 (2012)
C. T. MacDonald, J. H. Gibbs, and A. C. Pipkin, “Kinetics of Biopolymerization on Nucleic Acid Templates,” Biopolymers 6, 1 (1968)
B. Derrida, “Non-Equilibrium Steady States: Fluctuations and Large Deviations of the Density and of the Current,” J. Stat. Mech. P07023 (2007)
D. Chowdhury, L. Santen, and A. Schadschneider, “Statistical Physics of Vehicular Traffic and Some Related Systems,” Phys. Rep. 329, 199 (2000)
T. Chou, K. Mallick, and R. K. P. Zia “Non-Equilibrium Statistical Mechanics: From a Paradigmatic Model to Biological Transport,” Rep. Prog. Phys. 74, 116601 (2011)
G. M. Schütz, in Phase Transitions and Critical Phenomena Vol 19, edited by C. Domb and J. L. Lebowitz (Academic, New York, 2001)[Amazon][WorldCat]
R. A. Blythe and M. R. Evans, “Nonequilibrium Steady States of Matrix-Product Form: A Solver’s Guide,” J. Phys. A 40, 333 (2007)
H. Touchette, “The Large Deviation Approach to Statistical Mechanics,” Phys. Rep. 478, 1 (2009)
D. A. Adams, B. Schmittmann, and R. K. P. Zia, “Far-from-Equilibrium Transport with Constrained Resources,” J. Stat. Mech. P06009 (2008)
I. Neri, N. Kern, and A. Parmeggiani, “Totally Asymmetric Simple Exclusion Process on Networks,” Phys. Rev. Lett. 107, 068702 (2011)

About the Author

Andrea Parmeggiani is a professor of theoretical physics and biophysics at the University of Montpellier 2, France. After studying physics at the University of Bologna and the École Polytechnique in Paris, he received his Ph.D. from the Université Denis-Diderot (Paris-VII), working at the Curie Institute on the stochastic description of molecular motors. In 2000, he joined Erwin Frey’s Group, conducting research at the Technical University Munich, Harvard University, and the Hahn-Meitner-Institut Berlin. During this time he developed a new class of driven lattice gas model that was inspired by motor protein transport. Since moving to Montpellier in 2003, he has been working on biologically inspired problems related to statistical physics and stochastic processes.