The ABC of Aharonov Effects

Klaus Richter

Viewpoint

The ABC of Aharonov Effects

Klaus Richter

Institut für Theoretische Physik, Universität Regensburg, D-93040 Regensburg, Germany

February 21, 2012• Physics 5, 22

Controlling the spin and geometric phase of electrons in a semiconductor ring.

Figure caption — **Figure 1:** Sketch of a mesoscopic ring conductor, based on a two-dimensional electron gas in a layered semiconductor, and coupled to two leads. Rashba spin-orbit interaction couples the electron spin to an effective radial magnetic field (blue) perpendicular to the electron momentum (red) and to the electric field associated with the interface between the two semiconductor structures. For finite spin-orbit coupling, the electron spin cannot adiabatically maintain a fixed orientation with respect to this radial field but precesses around a guiding vector that itself tracks around a conical surface with opening angle $θ$ [see Eq. (1)]. (True adiabaticity would correspond to $θ = 90$ °.)

An electron traveling through an electric field experiences, in its rest frame, a magnetic field that interacts with the electron’s magnetic moment. This interaction is the basis of spin-orbit coupling, which causes a splitting of the energies of electrons in atoms depending on their spin state. In the case of electrons traveling along an interface between two different semiconductors, the transition from one conduction-band energy to another manifests itself as a local electric field that gives rise to a spin-orbit interaction. Here, the resulting momentum-dependent spin splitting is known as the Rashba effect [1]. Because the magnitude of the effect depends on the junction parameters and can be controlled by an external electric field, the Rashba interaction offers a promising tool for “spin-orbitronics,” in which spins can be manipulated through purely electrical mechanisms.

Electrons spins can also be manipulated by giving them a geometric or Berry phase [2]. The Aharonov-Casher effect [3], in which magnetic dipoles travel around a tube of electric charge, can be regarded as a special case of a Berry phase. The Aharonov-Casher effect is dual to the well-known Aharonov-Bohm effect [4], in which charged particles making a closed circuit around a tube of magnetic flux acquire a nonzero phase (see 22 July 2011 Focus story). Writing in Physical Review Letters, Fumiya Nagasawa and his colleagues at Tohoku University in Sendai, Japan [5] now report experiments where both the Rashba effect and Berry phases play essential roles. By measuring interference patterns produced by electrons traveling coherently in opposite directions around mesoscopic (micron-sized) layered semiconductor rings that exhibit strong Rashba spin-orbit coupling, they not only detect an Aharonov-Casher phase difference but also distinguish contributions coming from dynamical and topological influences on spin. Most notably, the experiment demonstrates precise control and detection of spin geometric phases, a capability that could lead the way to topological electronics.

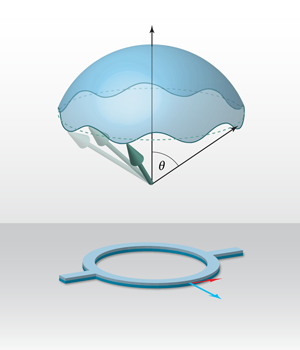
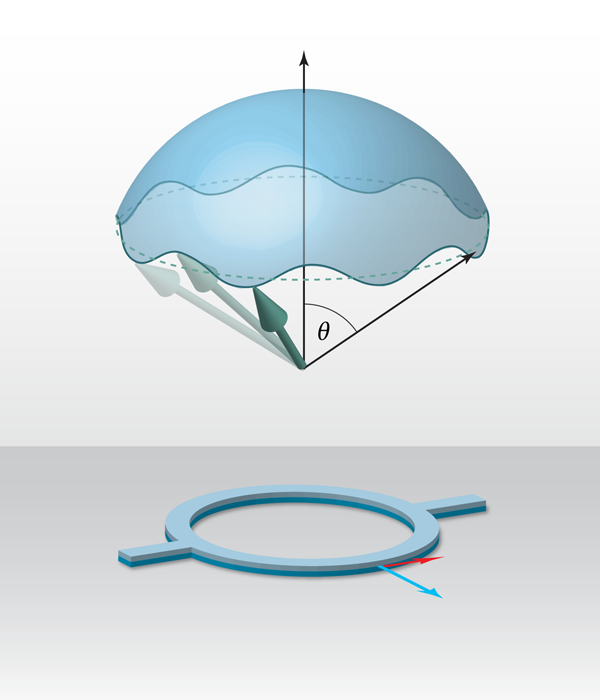
An electron making a complete circuit of a ring conductor immersed in a strong radial magnetic field acquires a geometric phase $- π$ , since the Berry phase for a spin- $1 / 2$ particle is minus half of the solid angle, here $2 π$ , traversed by the rotating spin as it follows the field. The coherent mesoscopic ring conductors studied by Nagasawa et al. [5] therefore appear to be ideally suited for observing this geometric phase, as long as a strong magnetic field with an azimuthal component is present. This is where Rashba spin-orbit coupling in a two-dimensional electron gas comes into play, as it can be viewed as the coupling of electron spin’s magnetic moment to an effective magnetic field ${\vec{B}}_{so}$ , as described in the introduction. According to Biot-Savart’s law, this field points perpendicular to the electron momentum $\vec{p}$ and perpendicular to the local (Rashba) electric field. Since the latter is oriented perpendicular to the two-dimensional electron gas, ${\vec{B}}_{so} \sim α \vec{p} \times {\vec{e}}_{z}$ , where $α$ is the gate-tunable spin-orbit strength. For electrons moving in the ring, this spin-orbit field is indeed radially oriented, as indicated in the Fig. 1.

An additional prerequisite for an electron to acquire a geometric phase is that it must move adiabatically, meaning, in this case, that it moves slowly enough that the spin’s magnetic moment stays aligned (or anti-aligned) with the local inhomogeneous magnetic field. This requires a separation of time scales: The Larmor frequency of spin precession, $ω_{so} = 2 μ B_{so} / ħ \sim α p$ , must be large compared to the frequency $ω = p / (m r)$ of revolution around a ring of radius $r$ [6]:

Adiabaticity is therefore favored by a strong spin-orbit interaction and a large but phase-coherent ring.

Although Rashba coupling can be considerable, as, for instance, in the $InAlAs / InGaAs$ heterostructures used by Nagasawa et al., true adiabaticity cannot be achieved. When the spin-orbit interaction is finite, the electron spin cannot maintain strict alignment with the radial in-plane magnetic field, but can be viewed as following a cone with effective opening angle $θ$ (see Fig. 1). The associated solid angle leads to a phase $- π (1 - cos θ)$ . This generalization of the Berry phase in the nonadiabatic case is often referred to as the Aharonov-Anandan phase [7]. Recalling that spin-orbit coupling originates from an electrical field, this geometric phase can also be regarded as an Aharonov-Casher phase for a (spin) magnetic momentum moving in the presence of an electrical field. Together with the phase of the Aharonov-Bohm effect, the dual to the Aharonov-Casher effect, these three related phases may be said to represent the ABC of Aharonov effects.

Interference between electron waves traveling clockwise and counterclockwise around a phase-coherent semiconductor ring leads to variation in the electrical conductivity of the ring with the strength of an applied perpendicular magnetic field. Magnetoconductance measurements should bear the fingerprint of all three effects, Aharonov-Anandan, Aharonov-Bohm, and Aharonov-Casher [8], and Nagasawa et al. cite a number of experiments revealing evidence for spin-orbit induced phase effects.

However, clear-cut detection of the purely geometric part of the Aharonov-Casher phase, $- π (1 - cos θ)$ , is difficult because an electron wave traversing the ring also acquires a dynamical phase of $π tan θ sin θ$ [6], arising from the additional spin precession driven by the local field. Nagasawa et al. [5] succeeded in separating out the geometric Aharonov-Casher phase from the other effects of the spin-orbit interaction and determining quantitatively the associated phase shift.

To do this, they used lithography and etching to create arrays of typically $50 \times 50$ micron-sized rings from a layered $InAlAs / InGaAs$ film. By measuring the resistance of an array of rings, nongeneric features from individual rings are averaged out. Nagasawa et al. conducted a series of experiments on arrays of rings whose diameters varied from about $1 / 2$ to $1$ micron, with different external field magnitudes, and with the spin-orbit coupling strength varied through a top-gate voltage on the arrays. They found remarkably clean oscillations in the ring resistance, and by analyzing the way these oscillations changed in response to the experimental parameters, they were able to distinguish and measure, for the first time in ring experiments, the pure spin-geometrical part of the phase.

Such geometrical phases are of wide significance in charge and spin transport. For instance, the surface states of a topological insulator are protected against backscattering from disorder through a Berry phase [9]. While such Berry phases are often intrinsically fixed, the ring experiments open up an interesting opportunity to steer geometric phases in a controlled way through the system geometry and various other tunable parameters. Besides those used by Nagasawa et al., additional knobs to control the phase could be other types of spin-orbit coupling or an in-plane magnetic field. Experiments of the type Nagasawa et al. describe represent promising mesoscopic labs for devising and engineering spin topological phases.

Acknowledgments

I acknowledge financial support from Deutsche Forschungsgemeinschaft through Research Unit FOR 1483.

References

E. I. Rashba, Fiz. Tverd. Tela (Leningrad) 2,1224 (1960); [Sov. Phys. Solid State 2, 1109 (1960)]
M. V. Berry, Proc. R. Soc. London A 392, 45 (1984)
Y. Aharonov and A. Casher, Phys. Rev. Lett. 53, 319 (1984)
Y. Aharonov and D. Bohm, Phys. Rev. 115, 485 (1959)
F. Nagasawa, J. Takagi, Y. Kunihashi, M. Kohda, and J. Nitta, Phys. Rev. Lett. 108, 086801 (2012)
D. Frustaglia and K. Richter, Phys. Rev. B 69, 235310 (2004)
Y. Aharonov and J. Anandan, Phys. Rev. Lett. 58, 1593 (1987)
H. Mathur and A. D. Stone, Phys. Rev. Lett. 68, 2964 (1992)
M. Z. Hasan, Physics 3, 62 (2010)

About the Author

Klaus Richter is a Professor of Theoretical Physics at the University of Regensburg, Germany. His research interests range from mesoscopic physics, spintronics, and molecular electronics to transport of cold atoms and quantum chaos. He obtained his Ph.D. at the University of Freiburg, Germany, in 1991. After postdoctoral stays at the University Paris-Sud in Orsay (France) and University of Augsburg (Germany) he spent five years as the head of a research group at the Max Planck Institute for the Physics of Complex Systems in Dresden, Germany. In 2001 he took up a Chair in Condensed Matter Theory in Regensburg. He was spokesperson of the German Physical Society’s Division for “Dynamics and Statistical Physics” and is designated spokesperson of its Condensed Matter Section.