Spins Made to Order in Low Dimensions

Michele Governale; Ulrich Zülicke

Viewpoint

Spins Made to Order in Low Dimensions

Michele Governale and Ulrich Zülicke

School of Chemical and Physical Sciences and MacDiarmid Institute for Advanced Materials and Nanotechnology, Victoria University of Wellington, Wellington 6140, New Zealand

March 19, 2012• Physics 5, 34

Coulomb interactions in the presence of spin-orbit coupling can stabilize ferromagnetic order.

Figure caption — **Figure 1:** Pictorial representation of the RKKY mechanism. Interaction between local moments, $I$ , is mediated by free charge carriers with local spin-density $S$ .

The quantum liquid formed by charge carriers in a conductor is a very excitable system [1]. Besides carrying electric current and screening electromagnetic fields, it can mediate magnetic interactions between stationary microscopic magnetic moments embedded in its host material (such as those from impurities). This so-called Ruderman-Kittel-Kasuya-Yosida (RKKY) mechanism [2] arises from a combination of quantum effects. First, the familiar exchange interaction causes a coupling of strength $J$ between any localized magnetic moment $I_{α}$ and the charge carriers’ spin density $S (R_{α})$ at its position $R_{α}$ . Second, the inherently wavelike properties of itinerant carriers in a conductor then result in a spatially extended magnetization pattern that generates a pairwise exchange interaction between the localized magnetic moments, described formally by an effective spin Hamiltonian

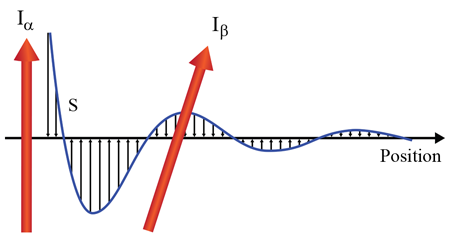
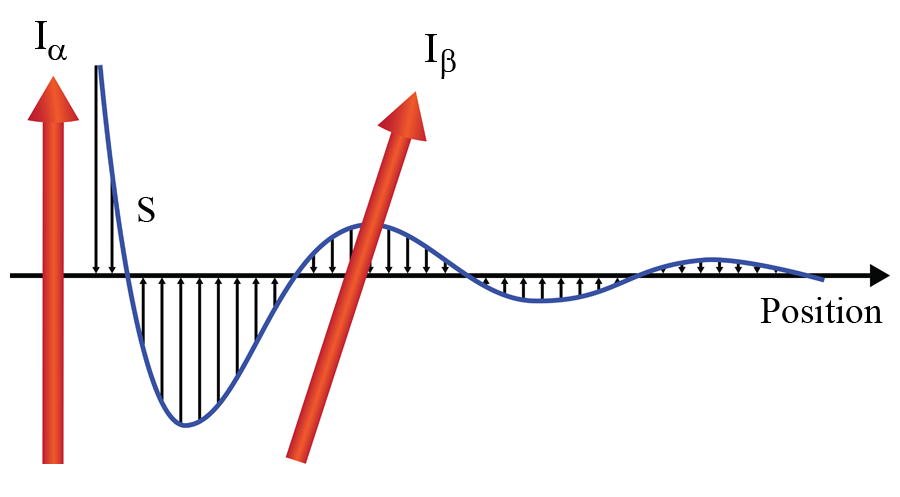
Here, the spin susceptibility $\underline{χ} (R, R^{'})$ , a property of the itinerant charge carriers, is a tensor that determines the interaction between the local moments. By definition, the spin susceptibility of a system encodes how charge carriers will adjust their spin-density profile in response to a spin-related perturbation. In a hypothetical scenario where the spin susceptibility is isotropic and sharply drops to zero for positions $R$ and $R^{'}$ separated by more that the typical distance between localized magnetic moments, the spin Hamiltonian (1) would be of the familiar Heisenberg-model form [2]. But because of its complex many-particle origin, the spin susceptibility of real materials is never just that simple. Already, in quite ordinary conductors where charge carriers are described by a parabolic band dispersion, its components turn out to be slowly decaying oscillatory functions of the distance $| R - R^{'} |$ with wavelength equal to half the Fermi wavelength of the conduction-electron system [2] (see Fig. 1 for an illustration of the RKKY mechanism). Introduce quantum confinement to a nanostructure, broken spin-rotational invariance, or interactions among the charge carriers, and understanding the spin response becomes a difficult task!

Now, Robert Żak from the University of Basel, Switzerland, and colleagues, in an article in Physical Review B [3] have found a way to take these factors into account. They present a comprehensive analysis for the spin susceptibility of a two-dimensional electron system with broken structural inversion symmetry in the presence of electron-electron interactions. It is known that broken inversion symmetry associated with confinement in a quantum well creates the so-called Rashba spin-orbit coupling [4]. The new insight obtained by Żak et al. [3] makes it possible to assess the stability of ferromagnetic order of nuclear or impurity spins in such a low-dimensional system [5]. The possibility to freeze nuclear magnetic moments in a ferromagnetic state would increase the prospect of realizing spin-based quantum bits having sufficiently long phase-coherence times. On a more fundamental level, the work identifies new features resulting from the interplay of interactions and spin-orbit coupling that make the real-space structure of the spin susceptibility even more interesting than was already the case for noninteracting electrons [6–8] and holes [9].

Now let us look in more detail at the model studied in Ref. [3]. Żak et al. consider two-dimensional electrons in the presence of electron-electron interaction and Rashba spin-orbit coupling. The uniform (zero wave vector) spin susceptibility for this model was studied by the same authors in Ref. [10]. In the new article, they consider the momentum-space Fourier transform of the spin susceptibility, which one needs to know for determining the stability of magnetic order in the system of localized impurities. As per the Mermin-Wagner theorem, continuous symmetries cannot be broken at finite temperature by short-range interactions in dimensions less than or equal to two. Recently, the applicability of this theorem has been extended to systems of localized spins with a magnetic interaction of the RKKY type, ruling out the formation of a magnetically ordered state in two and one dimensions [5]. However, magnetic order was found to be still possible if the charge carriers that mediate the magnetic interaction are subject to spin-orbit coupling. Therefore the inclusion of the Rashba spin-orbit coupling term in the model is crucial in the quest for facilitating a magnetic phase transition. Spin-orbit coupling breaks spin-rotational invariance, usually resulting in anisotropies of the uniform spin susceptibility, as is the case for two-dimensional hole gases [9]. This does not happen for noninteracting two-dimensional electrons subject to the Rashba spin-orbit coupling at zero temperature, where the uniform spin susceptibility tensor is still found to be isotropic [10].

However, the spin-orbit coupling term alone does not lead to a magnetically ordered state due to the presence of spin-wave excitations (the so-called magnons) in the localized spin system. Whether the ordered state is destabilized by spin-wave excitations depends on the relation between the energy needed for a given excitation and its wavelength. This relation is called the magnon dispersion and it is determined by the form of the spin susceptibility tensor or, more specifically, by its momentum-space Fourier transform. This brings us to the other ingredient of the model, the Coulomb interaction between the charge carriers, which affects the spin-susceptibility tensor and could stabilize the magnetic order. In Ref. [10] it was found that the electron-electron interaction in conjunction with the Rashba spin-orbit coupling breaks the isotropy of the uniform spin susceptibility, favoring the alignment of the localized spins in the direction perpendicular to the plane of the charge carriers (Ising ferromagnet). In the current article [3], it is shown that in the presence of both electron-electron interaction and spin-orbit coupling, the spin susceptibility in real space exhibits new oscillations with a wavelength equal to the Rashba spin precession length of the two-dimensional electron gas.

More significantly, the importance of the work lies in the detailed analysis of the effect of the interplay of spin-orbit coupling and electron-electron interaction on the stability of the magnetic ordered state. The presence of a two-particle interaction complicates the problem substantially, and a common approach in this situation is to perform a perturbative expansion in the interaction strength by means of a diagrammatic technique. The corrections to the spin-susceptibility tensor in second order in the interaction strength are not sufficient to ensure the stability of the ordered state. Żak et al. investigate higher order processes in the Coulomb interaction in a scheme where a particular subset of all possible diagrams is included. The good news is that they identify a process that, for certain parameter values, leads to the stability of the ferromagnetic order.

The authors envision that their work can have important consequences for the realization of qubits based on spins in quantum dots, as freezing the nuclear spins in a ferromagnetic state would drastically reduce decoherence in this type of systems. However, their study has broader implications for low-dimensional magnets, whose features could be tailored by changing the physical environment (especially spin-orbit coupling and confinement) of the charge carriers that mediate the interaction.

References

G. Giuliani and G. Vignale, Quantum Theory of the Electron Liquid (Cambridge University Press, Cambridge, 2005)[Amazon][WorldCat]
T. Moriya, Spin Fluctuations in Itinerant Electron Magnetism (Springer, Berlin, 1985)[Amazon][WorldCat]
R. Żak, D. L. Maslov, and D. Loss, Phys. Rev. B 85, 115424 (2012)
R. Winkler, Spin-Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems (Springer, Berlin, 2003)[Amazon][WorldCat]
D. Loss, F. L. Pedrocchi, and A. J. Leggett, Phys. Rev. Lett. 107, 107201 (2011)
H. Imamura, P. Bruno, and Y. Utsumi, Phys. Rev. B 69, 121303 (2004)
D. F. Mross and H. Johannesson, Phys. Rev. B 80, 155302 (2009)
S. Chesi and D. Loss, Phys. Rev. B 82, 165303 (2010)
T. Dietl, A. Haury, and Y. Merle d’Aubigné, Phys. Rev. B 55, 3347 (1997)
R. A. Żak, D. L. Maslov, and D. Loss, Phys. Rev. B 82, 115415 (2010)

About the Authors

Michele Governale is Associate Professor of Physics at Victoria University of Wellington and a Principal Investigator at the MacDiarmid Institute for Advanced Materials and Nanotechnology (a New Zealand Centre of Research Excellence). After obtaining his Ph.D. from the University of Pisa in Italy in 2001, he has held postdoctoral positions at the University of Karlsruhe (now KIT), Scuola Normale Superiore in Pisa, Ruhr-Unversität Bochum, and Duisburg-Essen University. In 2009 he moved to Victoria University of Wellington in New Zealand, where he is currently based. His present research focuses on the theory of quantum transport in nanostructures, spin-dependent phenomena, and hybrid normal-superconducting systems.

Ulrich Zülicke is a Professor of Physics at Victoria University of Wellington and a Principal Investigator at the MacDiarmid Institute for Advanced Materials and Nanotechnology. After obtaining his Ph.D. from Indiana University in 1998, he undertook postdoctoral research at the University of Karlsruhe in Germany and has held permanent academic positions at Massey University in New Zealand from 2003 until 2011. His current research is focused on the theoretical description of mesoscopic and low-dimensional systems, spins in semiconductors, and graphene.