Pushing Bits Through a Spin Wire
In the quest to use spin for quantum communication, researchers are constantly looking for new types of magnetic phases. A promising route for this control in solids is to exploit vector spin chirality. This is a pseudovector quantity formed by two neighboring atoms’ electronic spins that breaks parity and mirror symmetries. It is usually present together with cycloidal magnetism, but can be exploited as a sort of independent, hidden order parameter in the context of magnetism [1,2]. Recent searches for magnetically induced ferroelectricity, or multiferroics, have proven that this quantity is linearly coupled to, and probed by, the electric polarization because of the relativistic spin-orbit coupling [3]. Thus the coupling between vector spin chirality and the electric polarization might provide a route to an efficient electric control of magnetism for applications. Furthermore, this coupling also has potential application for spintronics devices, in the form of finite spin systems hosted by artificial atomic structures deposited on a surface [4,5]. Now, writing in Physical Review Letters, Matthias Menzel at the University of Hamburg, Germany, and colleagues show that iron biatomic chains, which should have the requisite spin spiral as its ground state, could be an excellent platform for such devices [6]. Combining calculations with scanning tunneling microscopy (STM) images of these iron chains, which behave as “spin wires,” the authors suggest such systems could be useful for transmitting bits of magnetic information.
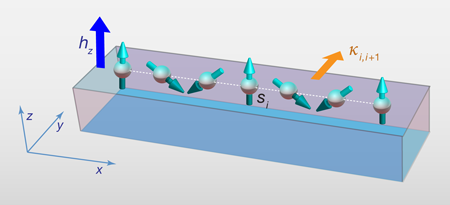
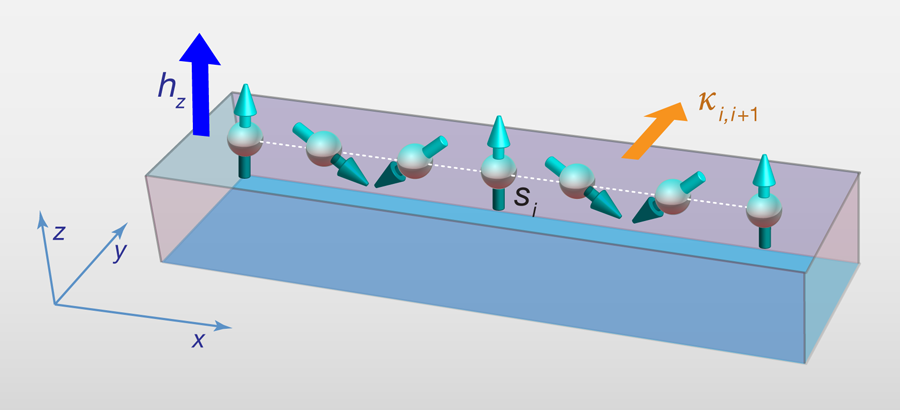
To engineer finite-length spin cycloids with a particular magnetic structure, it is necessary to balance the antisymmetric Dzyaloshinskii-Moriya spin interactions (which are induced by the structure of whatever the spins are lying on) with the symmetric exchange interactions. In such spin cycloids, the vector spin chirality, or the direction of the cycloidal correlation, is uniquely determined, even at high temperatures. This stands in sharp contrast to conventional cycloidal magnets, where the order is induced by a spontaneous symmetry breaking under geometrical frustration of the symmetric exchange interactions, but is not a priori determined. Hence, in a finite wire, vector spin chirality might allow for an immediate transmission of a change of an edge spin direction to the other edge, without an appreciable change in the electric charge degrees of freedom and a formation of vector-chiral domain walls. This is what is to be expected for efficient operations of writing/reading the spin degrees of freedom with low dissipation.
Menzel et al. probed the spin chains with spin-polarized STM, using magnetic and nonmagnetic tips under the out-of-plane magnetic field of at . Only with a magnetic tip, they observed a three-period modulation along the spin chains (see Fig. 1), which look uniform and featureless with a nonmagnetic tip. This represents evidence that the observed spatial modulation reflects the magnetic structure, which is stabilized under the magnetic field. To understand the origin of the magnetic structure they observed, the authors also performed first-principles calculations for iron atomic chains deposited on an iridium surface. The Dzyaloshinskii-Moriya interaction is mainly induced by the broken inversion and mirror symmetries at the surface, and it drives the iron spins from the otherwise uniform or staggered structure. The result of the simulations is a three-period cycloidal magnetic structure with the spiral plane spanned by the chain and the out-of-plane directions, so the simulations are consistent with the team’s spin-polarized STM results. The small out-of-plane magnetic field is necessary to quench the thermal and dynamical fluctuations over the finite spin chains, as the authors confirmed with Monte-Carlo simulations.
Viewed over the whole chain, the spins are correlated with a nearly fixed vector spin chirality, however, at zero magnetic field, there is no preferred direction for the spins at any temperature. This fact provides a finite-temperature, finite-size version of vector-chiral ordered spin liquids, which are found to be robust in frustrated spin chains [7]. A particularly rare feature of utilizing an open finite-size chain of – spins is that all the spins along the chain can be inverted by inverting the out-of-plane magnetic field, as the authors reveal by spin-polarized STM images with a magnetic tip at K. Their first-principles calculations also show that it is the spins at the edges that are responsible for the magnetization and thus the susceptibility. This suggests that if it is possible to invert the out-of-plane magnetic field locally acting at either edge of the chain, a spin flip would occur at one edge and propagate to the other (or at least as far as the spins were correlated). Since the total Zeeman energy is gained only at the edges in this antiferromagnetic spin spiral, in contrast to the case of a ferromagnet, spins can efficiently change their directions. The authors also verified this idea by using another device structure, where a chain of ferromagnetically polarized cobalt atoms are attached to one of the ends of the iron spin chains on an iridium surface. For these devices, spin-polarized STM images also show a three-period modulation in the iron spin chain, without applied magnetic field, again suggesting the spin spiral state along the iron chain. This indicates that the ferromagnetic cobalt atoms pin the edge spin in space and time, and then specify the directions of all the spins to the other edge, resulting in a transmission of information on the spin direction of ferromagnetic cobalt spins.
Unlike many other spintronics approaches, the authors’ proposed way of transferring information about the spin direction from one end of a spin chain to the other does not suffer from significant dissipative currents of electronic charge and spin along the direction of propagation, namely, the chain direction. Such low-energy-consumption devices are certainly advantageous applications. This work will form a cornerstone of realizing a highly functional spintronics device for information transfer, and contribute to a new field of manipulating further nontrivial spin systems implemented in artificial structures on the surface.
References
- J. Villain, J. Phys. C 10, 4793 (1977)
- H. Kawamura, J. Phys. Condens. Matter 10, 4707 (1998)
- T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima, and Y. Tokura, Nature 426, 55 (2003)
- C. F. Hirjibehedin, C. P. Lutz, and A. J. Heinrich, Science 312, 1021 (2006)
- A. A. Khajetoorians, J. Wiebe, B. Chilian, and R. Wiesendanger, Science 332, 1062 (2011)
- M. Menzel, Y. Mokrousov, R. Wieser, J. E. Bickel, E. Vedmedenko, S. Blügel, S. Heinze, K. von Bergmann, A. Kubetzka, and R. Wiesendanger, Phys. Rev. Lett. 108, 197204 (2012)
- S. Furukawa, M. Sato, and S. Onoda, Phys. Rev. Lett. 105, 257205 (2010)