Quantum Dipolar Gases in Boson or Fermion Flavor

Bruno Laburthe-Tolra

Viewpoint

Quantum Dipolar Gases in Boson or Fermion Flavor

Laboratoire de Physique des Lasers, UMR 7538 CNRS, Université Paris 13, 99 Avenue J.-B. Clément, 93430 Villetaneuse, France

May 21, 2012• Physics 5, 58

Lanthanide atoms are offering the best opportunities to study the effects of strong dipolar interactions in a quantum gas.

Figure caption — **Figure 1:** Dipolar interactions in a quantum gas of bosons or fermions. (a) The interaction between two particles with large dipole moments has a characteristic $d$ -wave symmetry. (b) In a Bose-Einstein condensate, this interaction causes the gas to implode with a similar $d$ -wave symmetry, as shown here for a gas of erbium- $168$ [2]. (c) In comparison, a quantum gas of fermions is stable, as shown for dysprosium- $161$ [1].

At extremely low temperatures, the properties of an atomic gas of bosons (atoms with integer spin) are dramatically different from those of a gas of fermions (atoms with half-integer spin). A confined gas of bosons can be cooled into a Bose-Einstein condensate (BEC), where all of the atoms fall into the same quantum mechanical state to form a macroscopic matter-wave. Fermionic atoms, however, avoid each other. At very low temperatures, a trapped gas of these atoms forms a Fermi sea, where the atoms fill the allowed energy levels of the gas up to the so-called Fermi level. Although the low-temperature states of boson and fermion gases result from purely quantum statistical effects, interactions between the atoms can lead to collective behavior, like superfluidity.

In Physical Review Letters, two experimental groups report they have prepared cold quantum gases in which the atoms have unusually strong magnetic dipolar interactions: In an experimental first, scientists at the University of Illinois, Urbana-Champaign, and Stanford University, California (M. Lu et al.), have shown they can cool fermionic dysprosium- $161$ to form a Fermi sea of particles [1], while a group at the University of Innsbruck, Austria (K. Aikawa et al.), have prepared a cold quantum gas of erbium- $168$ [2], which is a boson. In both systems, the quantum statistics of the particles (bosons or fermions), and the dipolar interactions between them, are probed by analysing how these gases expand after being released from a trap.

Most cold-atom experiments are performed on gases made of alkali atoms, which have one valence electron in an $s$ orbital. The predominant (van der Waals) interaction between neutral alkali atoms decreases with interparticle distance so quickly (as $1 / r^{6}$ ) that it can safely be described with an effective contact interaction potential $\propto δ (r)$ . In other words, the atoms do not see each other until they touch.

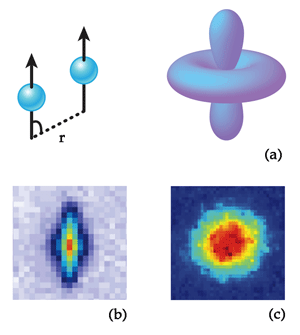
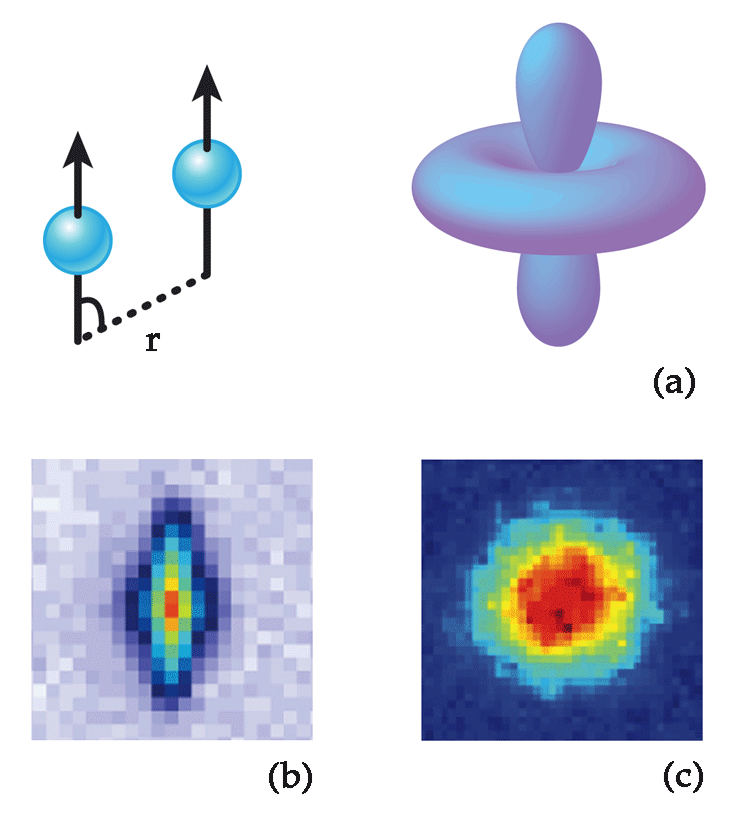
However, atoms or molecules with large permanent magnetic moments or field-induced electric dipole moments also interact through dipole-dipole interactions. These interactions are anisotropic and long ranged [Fig.1(a)], similar to the interaction between classical bar magnets. The properties of a quantum degenerate gas made of atoms interacting with each other via dipole-dipole forces will be drastically different compared to one with only van-der-Waals-type short-range interactions [3].

The study of dipolar quantum gases began when experimentalists at the University of Stuttgart were able to make a BEC of chromium, which has a magnetic moment of $6$ Bohr magnetons ( $μ_{B}$ ) [4]. These researchers used Feshbach resonances—an effective interaction between two atoms can be controlled with a magnetic field—to tune the strength of contact interactions, and observed that when dipolar forces dominate, their attractive part causes a characteristic $d$ -wave-like implosion of the condensate [5], provided the geometry of the trap they use to confine the atoms is not too oblate (see 18 August 2008 Viewpoint). Work in our group in France later showed that the trapping geometry has an impact on the spectrum of collective excitations of dipolar BECs [6].

Compared with chromium, which is a transition metal, the lanthanide atoms have even larger magnetic moments: erbium has a moment of $7 μ_{B}$ and dysprosium has a moment of $10 μ_{B}$ . (The strength of dipolar interactions between atoms is proportional to the square of the dipole moment, so even this seemingly small increase has a big effect.) In fact, dysprosium is heralded as “the” most magnetic atom. Interest in lanthanides began in 2006, when researchers at NIST demonstrated for the first time that erbium atoms could be cooled with lasers [7]. Laser cooling relies on an atom preferentially absorbing a photon from a laser beam propagating opposite to the atoms’ velocity: the photon gives the atom a momentum kick, and since the emitted photon will have a random momentum, on average this kick slows the atom down. To bring a thermal atom to rest, it typically has to absorb tens of thousands of photons, and this can only happen if the excited atom quickly emits a photon and returns to its original electronic state. Erbium atoms, however, don’t have a closed electronic transition, so the demonstration that they could be laser cooled came as a surprise. It turns out that because erbium atoms have such a large dipole moment, they stay confined in a magneto-optical trap long enough to decay to their ground state, after which laser cooling becomes efficient again.

The Stanford group has been able to take advantage of much of what was learned about cooling erbium and apply it to cooling dysprosium [1,8]. Similarly, the Innsbruck group’s production of erbium BECs relies on very efficient laser cooling down to temperatures in the low microkelvin range. At such low temperatures, they can efficiently load the cold atoms into an optical dipole trap, where they undergo evaporative cooling, a process in which the most energetic atoms are selectively removed from the finite-depth trap, and the remaining atoms re-thermalize at a lower temperature. With this method, the team is able to produce an erbium BEC after only $5$ seconds.

In these early experiments, both groups have characterized the properties of a quantum gas composed of atoms with large dipole moments. Aikawa et al. show that erbium- $168$ atoms have as many as six Feshbach resonances when the magnetic field is scanned from $0$ to $3$ gauss. They are able to use these low-magnetic-field Feshbach resonances to drive the system into a regime where dipolar interactions dominate, and hence reproduce the characteristic $d$ -wave collapse [Fig.1(b)] first seen in chromium [5]. However, an important technical simplification is that Aikawa et al. were able to study the $d$ -wave implosion in erbium around $1$ gauss, while a much higher field (more than $500$ gauss) was needed for chromium. With this lower field, it might be possible to do experiments where the sign of the dipolar interactions is reversed by time-modulating the orientation of the magnetic field [9]. In general, the presence of low-lying Feshbach resonances opens extraordinary possibilities for studying almost purely dipolar gases. In such systems, rotonlike excitations, bright solitons stable in 2D geometry, or new vortex patterns in rotating dipolar gases [3] are predicted to occur.

Lu et al.’s work represents a new qualitative step. Being the first to produce a Fermi sea of interacting dipolar atoms, they have achieved a long-pursued goal. (For example, researchers have tried to do the same thing with $K-Rb$ molecules, which have a large field-induced electric dipole moment [10].) One important property of polarized fermions at low temperature is that $s$ -wave scattering is forbidden by symmetry. A polarized dysprosium Fermi sea is therefore a purely dipolar quantum gas, where contact interactions are absent. Also, a Fermi sea of atoms has an intrinsic stability because only those particles near the Fermi level can be easily excited. Thus, unlike the purely dipolar BEC of erbium atoms, which is unstable and implodes, the cloud of dysprosium remains stable [Fig.1(b),(c)].

By studying dysprosium gas as it cools by evaporation, Lu et al. are able to show the importance of dipolar collisions: polarized dipolar Fermions thermalize, and therefore collide, whereas there would be no collisions for fermionic particles with only short-range interactions. Having produced this Fermi sea of dysprosium, the next goal will be to observe the effect of dipolar interactions. Although the strength of the dipolar interaction compared to the Fermi energy is still somewhat small, it might still lead to a Fermi surface distortion at the percent level, which would be a completely new feature. Dipolar Fermi gases are expected to exhibit novel anisotropic Fermi liquid properties, as well as liquid-crystal states, phases with density modulation, or even supersolidity.

Taken together, the work of Lu et al. and Aikawa et al. offers an exciting opportunity to study a large spectrum of phases that have been predicted to occur in strongly dipolar quantum gases.

References

M. Lu, N. Q. Burdick, and B. L. Lev, Phys. Rev. Lett. 108, 215301 (2012)
K. Aikawa, A. Frisch, M. Mark, S. Baier, A. Rietzler, R. Grimm, and F. Ferlaino, Phys. Rev. Lett. 108, 210401 (2012)
M. A. Baranov, “Theoretical Progress in Many-body Physics with Ultracold Dipolar Gasses,” Phys. Rep. 464, 71 (2008); T. Lahaye, C. Menotti, L. Santos, M. Lewenstein, and T. Pfau, “The Physics of Dipolar Bosonic Quantum Gasses,” Rep. Prog. Phys. 72, 126401 (2009)
A. Griesmaier, J. Werner, S. Hensler, J. Stuhler, and T. Pfau, “Bose-Einstein Condensation of Chromium,” Phys. Rev. Lett. 94, 160401 (2005)
T. Lahaye, J. Metz, B. Fröhlich, T. Koch, M. Meister, A. Griesmaier, T. Pfau, H. Saito, Y. Kawaguchi, and M. Ueda, “d-wave Collapse and Explosion of a Dipolar Bose-Einstein Condensate,” Phys. Rev. Lett. 101, 080401 (2008)
G. Bismut, B. Pasquiou, E. Maréchal, P. Pedri, L. Vernac, O. Gorceix, and B. Laburthe-Tolra, “Collective Excitations of a Dipolar Bose-Einstein Condensate,” Phys. Rev. Lett. 105, 040404 (2010)
J. J. McClelland and J. L. Hanssen, “Laser Cooling without Repumping: A Magneto-Optical Trap for Erbium Atoms,” Phys. Rev. Lett. 96, 143005 (2006)
M. Lu, N. Q. Burdick, S. H. Youn, and B. L. Lev, “Strongly Dipolar Bose-Einstein Condensate of Dysprosium,” Phys. Rev. Lett. 107, 190401 (2011)
S. Giovanazzi, A. Görlitz, and T. Pfau, “Tuning the Dipolar Interaction in Quantum Gases,” Phys. Rev. Lett. 89, 130401 (2002)
K. K. Ni, S. Ospelkaus, D. Wang, G. Quemener, B. Neyenhuis, M. H. G. de Miranda, J. L. Bohn, J. Ye, and D. S. Jin, “Dipolar Collisions of Polar Molecules in the Quantum Regime,” Nature 464, 1324 (2010)

About the Author

Bruno Laburthe-Tolra is a CNRS research assistant at Université Paris 13, France. He completed his Ph.D. in 2001 at Université Paris 11, and later worked at the National Institute of Standards and Technology, Gaithersburg. His current research interests include quantum degenerate gases in optical lattices, spinor and dipolar quantum gases.