An Extraordinary Josephson Junction
The combination of symmetry breaking effects, such as those occurring in magnets and superconductors, with topological order may result in remarkable new physics. Recent theoretical studies suggest that, in certain superconductors, exotic quasiparticle excitations can emerge that behave like Majorana fermions, charge-neutral quasiparticles that are their own antiparticles. In Physical Review Letters, Jimmy Williams at Stanford University, California, and colleagues [1] combine the superconducting Josephson effect, which is a profound consequence of symmetry breaking, with topological order in hybrid superconductor-topological insulator structures. The structure investigated by the authors exhibits unconventional behavior that may be related to the emergence of Majorana states.
In a Josephson junction, consisting of two superconductors separated by a thin nonsuperconducting barrier, symmetry breaking results in a supercurrent, i.e., a dissipationless current, that depends on the phase difference ( φ1-φ2) across the junction via the current-phase relation
where Ic is the critical current beyond which the superconductor reverts to the normal state.
The first example of topological order, the quantum Hall effect, was discovered in two-dimensional electron systems and theoretically understood in the early 1980s. Work in recent years has shown that topological order is more common than previously suspected and is realized in a class of materials called topological insulators. These are three-dimensional band insulators in which spin-orbit coupling leads to metallic surface states at every surface [2].
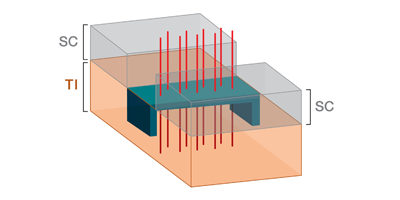
Williams et al. report unusual behavior in Josephson junctions made by depositing superconducting aluminum on top of bismuth selenide, a topological insulator (Fig. 1), leaving a small gap between the aluminum-covered regions. The authors apply an external magnetic field and analyze the dependence of the critical current Ic on the strength of the field. Their experimental results could be related to the exotic physics predicted to exist in this system.
The effect of the magnetic field can be understood through a simple optics analogy. When an electron moves across the Josephson junction, it picks up a phase difference if the two superconductors have a different phase. But the electron also picks up a phase from the magnetic field (more precisely, from the integral of the vector potential A along its path), and this second phase difference depends on the path in space taken by the electron. For a Josephson junction with uniform current density, the phase differences between paths induced by the magnetic field give rise to a Fraunhofer or single-slit diffraction pattern in the dependence of critical current on magnetic field. At certain field strengths, paths across the junction interfere destructively and the critical current is zero.
The most striking feature of the data of Williams et al. is that the dependence of critical current on field is dramatically different from the conventional Fraunhofer pattern. The first minima occur at smaller fields than expected from the geometrical area of the junction; this could be explained if the effective area of the junction is smaller than estimated or if the magnetic field in the junction area is increased through “flux focusing’’ via the Meissner repulsion of the field from the superconductors. (A control experiment using graphite rather than a topological insulator suggests that flux focusing is not the explanation.) What is more puzzling is that the shape of the curve is also very different from a Fraunhofer pattern. The authors suggest that the data indicate a deviation from the conventional current-phase relation [Eq. (1)] and could be a sign of unusual physics related to emergent Majorana fermions.
In order to discuss the remarkable physics that this experiment may be revealing, we need to recall relevant properties of topological insulators. Their surface state is an analog in one higher dimension of the conducting edge states in the quantum Hall and quantum spin Hall effects. Like graphene, the topological insulator surface state has zero effective mass for the electrons. Unlike graphene, the topological insulator surface state has an odd number of Dirac points where the Fermi surface collapses, and this difference has far-reaching consequences when the surface state is coupled to a superconductor.
Most superconductors, including both traditional superconducting metals and cuprates, will have bound electronic levels in a magnetic vortex. Previous theoretical work has suggested that a vortex in certain exotic superconductors might have a bound Majorana level, which can be understood as half of an ordinary bound level. Such states are the solid-state quasiparticle realization of Majorana fermions, for which intense research efforts have recently attempted to provide experimental evidence (see 15 March 2010 Viewpoint) [3]. It was pointed out by Fu and Kane [4], following a proposal in a different context by Sato [5], that the interface between a conventional superconductor and a topological insulator supports such Majorana levels in magnetic vortices, and that Majorana levels can lead to a modification of the Josephson effect. Briefly, the standard current-phase relation [Eq. (1)] is modified by the existence of Majorana quasiparticles; one consequence is that the magnetic flux periodicity of the observed current in a junction can be doubled.
In Williams et al.’s experiment, the dependence of critical current on magnetic field effectively performs an integration over the current-phase relation because different paths have different phase contributions from the field. The authors consider possible current-phase relations and compare the resulting field dependence to the experimental observations. The best fits, including the distinctive first notch in the data, are obtained from current-phase relations that are substantially different from Eq. (1).
The data reveal several unconventional features, including anomalous dependences of the critical current on junction size and on normal-state resistance. Non-Fraunhofer shapes of the critical current curve can be caused by nonuniform current injection, which might result from topological insulator behavior: if the sides of the topological insulator barrier carried current roughly as well as the top surface, this would lead to a superposition of one-slit and two-slit interference patterns that looks similar to the experimental data [6]. While this explanation depends on the topological insulator barrier having a surface state, it would not require any modification of the current-phase relation, but the multiple unusual features of the Williams et al. experiments suggest that a more unconventional explanation may be required. To explain the observed effects, the authors propose a phenomenological model based on the emergence of Majorana modes at the superconductor-topological insulator interface.
There are several groups—notably those at Purdue [7], Delft [8], and Weizmann [9]—whose work suggests Majorana fermions can be created using superconductors. In these experiments, a superconductor is combined with an ordinary semiconductor in a magnetic field, and features are observed that may be caused by a Majorana bound level, according to theoretical models. Other groups are exploring similar physics in certain phases of superfluid helium-3. Whichever route turns out to be more fruitful in the future, it is exciting to see that one of the most remarkable predictions of the theory of superconductivity, namely that a spinless electron or two-level system can be “fractionalized” into two Majorana quasiparticles, seems to be coming closer to experimental reality.
References
- J. R. Williams, A. J. Bestwick, P. Gallagher, S. S. Hong, Y. Cui, A. S. Bleich, J. G. Analytis, I. R. Fisher, and D. Goldhaber-Gordon, ”Unconventional Josephson Effect in Hybrid Superconductor-Topological Insulator Devices,” Phys. Rev. Lett. 109, 056803 (2012)
- For a review of 3D topological insulators see M. Z. Hasan and J. E. Moore, “Three-Dimensional Topological Insulators,” Ann. Rev. Cond. Mat. Phys. 2, 55 (2011)
- M. Franz, “Race for Majorana Fermions,” Physics 3, 24 (2010)
- L. Fu and C. L. Kane, “Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator,” Phys. Rev. Lett. 100, 096407 (2008)
- M. Sato, “Non-Abelian Statistics of Axion Strings,” Phys. Lett. B 575, 126 (2003)
- The author is grateful to H.-S. Sim and J. Bardarson for conversations regarding this point
- L. P. Rokhinson, X. Liu, and J. K. Furdyna, “Observation of the Fractional ac Josephson Effect: The Signature of Majorana Particles,” arXiv:1204.4212 (2012)
- V. Mourik, K. Zuo, S. M. Frolov, S. R. Plissard, E. P. A. M. Bakkers, and L. P. Kouwenhoven, “Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices,” Science 336, 1003 (2012)
- A. Das, Y. Ronen, Y. Most, Y. Oreg, M. Heiblum, and H. Shtrikman, “Evidence of Majorana Fermions in an Al-InAs Nanowire Topological Superconductor,” arXiv:1205.7073 (2012)