A SQUID Analog with a Bose-Einstein Condensate

Yuki  Sato

Viewpoint

A SQUID Analog with a Bose-Einstein Condensate

Yuki Sato

Rowland Institute at Harvard, Harvard University, Cambridge, MA 02142, USA

November 11, 2013• Physics 6, 123

Macroscopic quantum effects in Bose-Einstein condensates permit new kinds of ultrasensitive detectors.

Figure caption — **Figure 1:** (a) Superposition of horizontal light sheet and a rapidly moving vertical beam is used to create attractive potentials for BECs. By translating the vertical beam in the horizontal plane, Ryu *et al.* can “paint” an arbitrary trapping configuration. (b) Using this technique, Ryu *et al.* created a potential in the form of a loop interrupted by two thin barriers. (c) Absorption image of a BEC in this potential, resembling a dc-SQUID-like configuration.

Superconducting Quantum Interference Devices (specifically, dc-SQUIDs) are the world’s most sensitive sensors for magnetic flux. What lies at the heart of this quantum interference technology is the Josephson effect, which is a striking example of a macroscopic quantum phenomenon [1]. When two macroscopically coherent quantum systems such as superconductors are weakly coupled together, through a thin insulating layer for example, a direct current can appear across the junction with no applied voltage. This is known as the dc Josephson effect. As if that were not strange enough, if one tries to put a constant voltage across the junction, the direct current disappears and counterintuitively an alternating current now appears. This is known as the ac Josephson effect. By setting up a loop of a quantum system interrupted by a pair of such junctions, we can exploit these phenomena for interferometry. Magnetic flux acting on the electrons through a superconducting loop causes a phase shift between electric currents that flow across the two junctions and this interference alters the amplitude of the overall oscillation. As a result, dc-SQUIDs find application as ultrasensitive magnetometers [2].

In a neutral system, the role of magnetic field can be played by other effects such as rotational dynamics, and dc-SQUID analogs that work as rotation sensors have been implemented using superfluid helium—an uncharged fluid analog of superconductors [3,4]. Now, in a paper in Physical Review Letters, Changehyun Ryu and colleagues from Los Alamos National Laboratory, New Mexico, report the creation of a dc-SQUID analog using a Bose-Einstein condensed (BEC) atomic gas [5]. The result should not only encourage studies on BEC properties in complex arrangements but also accelerate the development of an array of cold atom “devices” that may be applied to various other investigations.

How can an ultracold gas act like a dc-SQUID? The Josephson effect relies on the sinusoidal nature of the relation between the current that flows and the relative phase that exists across the junction. In conventional dc-SQUIDs the flow is an electric current, whereas in BECs it is a mass current, and the relative phase is the difference in phase factors of the wave function on either side of the junction. In these macroscopic quantum systems, the relative phase evolves in time in response to the applied potential differences (voltage difference for superconductors, pressure and temperature differences for superfluid helium, and population difference between the two condensates for BECs). A constant potential difference, for example, leads to a relative phase that increases linearly in time, and through the sinusoidal current-phase relation, this then gives rise to an oscillating current. The nonlinear current-phase relation is a key signature of the leakage and the weak coupling of the two macroscopic wave functions.

To achieve this weak coupling, for superconducting systems, researchers employ junctions that are either a tunneling type (where electrons tunnel through a thin nonsuperconducting element) or a constriction type (where the junction is a superconductor, but its physical dimension is made small). For superfluid helium, dc-SQUID analogs are made with a toroidal container interrupted with a pair of constriction-type junctions.

In BEC systems, researchers have observed the Josephson phenomena with tunneling-type junctions made of thin barriers in single-weak-link geometries [6,7]. Wright et al. recently reported a vividly illuminating experiment that utilized a toroidal BEC interrupted with a single constriction-type junction [8] (see 10 January 2013 Synopsis). In that geometry, no interference takes place, but researchers investigated rich physics in a regime just outside of the Josephson regime where the atomic current as a function of relative phase was hysteretic but not purely sinusoidal.

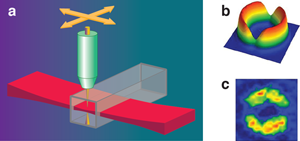
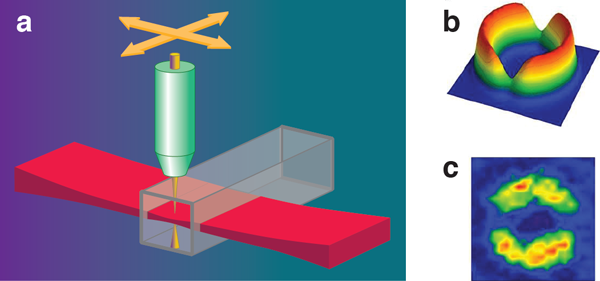
In paving a way towards the BEC version of the dc-SQUID, Ryu et al. used a technique that they developed several years ago for creating arbitrary potentials for static trapping and dynamical manipulation of BECs [9]. By rapidly moving a laser beam over a static light sheet that provides tight confinement, they effectively “paint” an attractive optical potential in an appropriate geometry (Fig. 1). Here the spatial resolution of the potential is on the order of a few micrometers, which allowed them to create a toroidal potential interrupted by a pair of tunneling-type Josephson junctions. They then moved the junctions circumferentially towards each other, a clever scheme proposed by Giovanazzi et al. [10].

If the junctions are moved slowly enough, atoms tunnel through them and keep the potential difference between the two sectors of the toroidal atomic cloud approximately zero. This is in close analogy to the dc Josephson effect, where a direct current appears across the junction with no driving potential difference. However, as the junction speed is ramped up, the tunneling current cannot respond quickly enough, and a finite potential difference develops at some critical velocity. The atomic current oscillation should then be driven by this energy difference with a frequency proportional to it, which is the ac Josephson effect.

In the absence of dissipation, no net current flows in this ac regime, as the current is only alternating. Hence for speeds any higher than the critical velocity, atoms simply become compressed on one side and expanded on the other side, which appears as a sudden change in the relative population difference in the two sectors of the toroid. Since the Josephson oscillation itself was too small to directly detect, the transition between the dc and ac Josephson effects was sought after to study the Josephson dynamics.

Ryu et al. measured the relative population difference as a function of the total atom number for several fixed rotational speeds of the junctions. Their data from the absorption images of a BEC indeed show dynamic behavior consistent with the system transitioning from dc to ac Josephson regimes, and the overall atom number dependence of atomic current at such transitions is in good agreement with the predictions of the Josephson dynamics. Although it is done indirectly, the current-phase relation is found to be sinusoidal through a simulation on the experiment.

The work of Ryu et al., along with that of Wright et al. [8], offers an exciting opportunity towards sophisticated atom circuits designed and implemented as meaningful tools. In various configurations with or without the Josephson junctions, the cold-atom system has the potential to form an ideal testing ground for phenomena seen in other analogous systems but now with more tunability. That is clear from this result, which advances the fundamental and thought-provoking analogy between the macroscopic quantum physics of superconductivity, superfluids, and BEC gases.

So what remains to be done? A lot, actually. One immediate step is simply more measurements, in particular, obtaining the junctions’ current-phase relation directly. With dynamic variations in the coupling strength, the relation between the atomic current and the relative phase across the junction should exhibit a smooth transition from a linear to sinusoidal shape as the system enters the Josephson regime. This might emerge in a series of destructive interference fringe measurements as the two sections of the BEC toroid are allowed to expand and overlap physically. Another truly revealing measurement would be to directly observe the Josephson oscillation itself in this multijunction system, as done in single-junction experiments, and to demonstrate that the oscillation frequency is proportional to the applied potential difference.

When a beam of light or matter is split and recombined while enclosing a finite area, physical rotation of the instrument leads to a difference in the path lengths in the two directions and gives rise to a rotation-induced phase shift. Through this celebrated Sagnac effect, combined with the quantization condition that the total phase change along a loop must be an exact integer multiple of $2 π$ , a BEC version of the dc-SQUID would function as a rotation sensor with potential applications in navigation, seismology, and geodesy. To explore such possibilities, the demonstration of double-path quantum interference via externally applied rotation may be in order. Studies along those lines should not only reveal intrinsic noises of the system configured as such a device but may also lead to the discovery of various nonlinear phenomena to enhance its sensitivity and utility.

References

B. D. Josephson, “Possible New Effects in Superconductive Tunnelling,” Phys. Lett. 1, 251 (1962)
J. Clarke and A. I. Braginski, The SQUID Handbook (Wiley-VCH, Weinheim, 2004)[Amazon][WorldCat]
O. Avenel, Yu. Mukharsky, and E. Varoquaux, “Superfluid Gyrometers,” J. Low Temp. Phys. 135, 745 (2004)
Y. Sato and R. Packard, “Superfluid Helium Quantum Interference Devices: Physics and Applications,” Rep. Prog. Phys. 75, 016401 (2012)
C. Ryu, P. W. Blackburn, A. A. Blinova, and M. G. Boshier, “Experimental Realization of Josephson Junctions for an Atom SQUID,” Phys. Rev. Lett. 111, 205301 (2013)
M. Albiez, R. Gati, J. Folling, S. Hunsmann, M. Cristiani, and M. Oberthaler, “Direct Observation of Tunneling and Nonlinear Self-Trapping in a Single Bosonic Josephson Junction,” Phys. Rev. Lett. 95, 010402 (2005)
S. Levy, E. Lahoud, I. Shomroni, and J. Steinhauer, “The a.c. and d.c. Josephson Effects in a Bose–Einstein Condensate,” Nature 449, 579 (2007)
K. C. Wright, R. B. Blakestad, C. J. Lobb, W. D. Phillips, and G. K. Campbell, “Driving Phase Slips in a Superfluid Atom Circuit with a Rotating Weak Link,” Phys. Rev. Lett. 110, 025302 (2013)
K. Henderson, C. Ryu, C. MacCormick, and M. Boshier, “Experimental Demonstration of Painting Arbitrary and Dynamic Potentials for Bose–Einstein Condensates,” New J. Phys. 11, 043030 (2009)
S. Giovanazzi, A. Smerzi, and S. Fantoni, “Josephson Effects in Dilute Bose-Einstein Condensates,” Phys. Rev. Lett. 84, 4521 (2000)

About the Author

Yuki Sato received his Ph.D. in physics from the University of California at Berkeley and is currently a principal investigator of the Applied Matter & Devices Group at the Rowland Institute at Harvard University. His research interests include quantum engineering with superfluidity and superconductivity, metamaterials and devices, mass transport dynamics in one-dimensional limit, and force/displacement sensing limits. He is a recipient of the Rowland Junior Fellowship at Harvard University.