Sharing Entanglement without Sending It

Christine Silberhorn

Viewpoint

Sharing Entanglement without Sending It

University of Paderborn, D-33098 Paderborn, Germany

December 4, 2013• Physics 6, 132

Three new experiments demonstrate how entanglement can be shared between distant parties without the need of an entangled carrier.

Figure caption — **Figure 1:** Three different experiments demonstrate the distribution of entanglement with a nonentangled carrier. The general scheme is to first initiate three photons or three light beams ( $A$ , $B$ , $C$ ) in separable states. Alice takes $A$ and $C$ and puts them through a kind of interference process, which creates a correlation between them, but not entanglement. The resulting $C$ is then sent to Bob, who combines it with his $B$ . In the final analysis, $A$ and $B$ are entangled, even though the carrier ( $C$ ) was never entangled with either.

To challenge the limited understanding of the then-young quantum theory, Einstein, Podolsky, and Rosen constructed, in 1935, their EPR Gedankenexperiment, in which they introduced entangled states that exhibit strange correlations over macroscopic distances [1]. By now we have learned that entangled states are an element of physical reality. They lie at the heart of quantum physics and can, in fact, be used as a powerful resource in emerging quantum technologies. Yet we find out in amazement that we have still not completely captured the full scope of the fascinating nature of entanglement. Three different international groups have now reported in Physical Review Letters [2–4] experiments of distributing entanglement between two distant parties by sending a nonentangled carrier. These arrangements instead place the carrier in a “cheaper,” so-called separable state, which exhibit correlations that can be established remotely between separated parties.

Entanglement is typically characterized by anomalously strong correlations between presently noninteracting parties, typically called Alice and Bob, which have normally interacted in the past. A common setup uses a nonlinear crystal to create an entangled pair of orthogonally polarized photons that are then sent separately, one to Alice and the other to Bob. In the field of quantum information science, the remote establishment of entanglement is key for most applications because it introduces purely nonclassical correlations and the counterintuitive nature of quantum physics. It enables such remarkable tasks as quantum teleportation, efficient quantum communication, fundamental tests of quantum physics, and long-distance quantum cryptography.

The quantum correlations associated with entanglement are not the only type of correlations that can occur in quantum systems. In order to give a rigorous definition of the “entangled” correlations, separable states have been introduced as the converse of entanglement [5]. Separable states are quantum states that can be prepared nonlocally, and yet they can be correlated to a certain degree. For example, Alice might polarize one photon in the vertical direction and tell Bob over the phone to polarize another photon in the horizontal direction. It is well confirmed that these photons (or other distant separable states) cannot be subsequently entangled by means of local operations and classical communication (LOCC) [6]. In this way, it seems clear that we can distinguish between entangled states as being quantum, and separable states as representing the classical world.

However, recent research has discovered that quantum physics does not stop surprising us with its counterintuitive properties. In 2003, Cubitt et al. [7] showed that sometimes separable states can actually be used to distribute entanglement between Alice and Bob. This is in strong contrast to any standard communication, where the information gained by the receiver can’t be greater than the information in the carrier. Bob, for example, can’t recover a color photo if all Alice sent was a black and white copy. But quantum information is unique in that entanglement can be sent using a cheaper—more generic—form of nonclassical correlations that can be characterized by a measure called quantum discord. A perfectly classical system has zero discord, whereas quantum systems can have varying amounts of discord, depending on the mixture of possible states they occupy. Recent work has shown that quantum discord can be an important form of currency in quantum information sharing when three or more systems are involved [8,9]. This raises the obvious question: Can we really observe such an entanglement distribution in experiments?

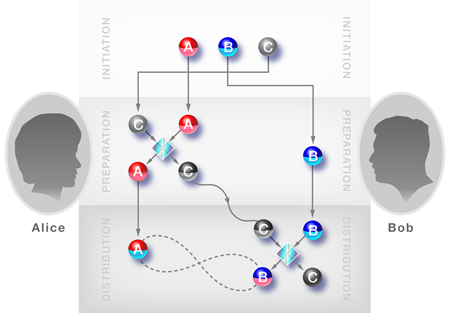
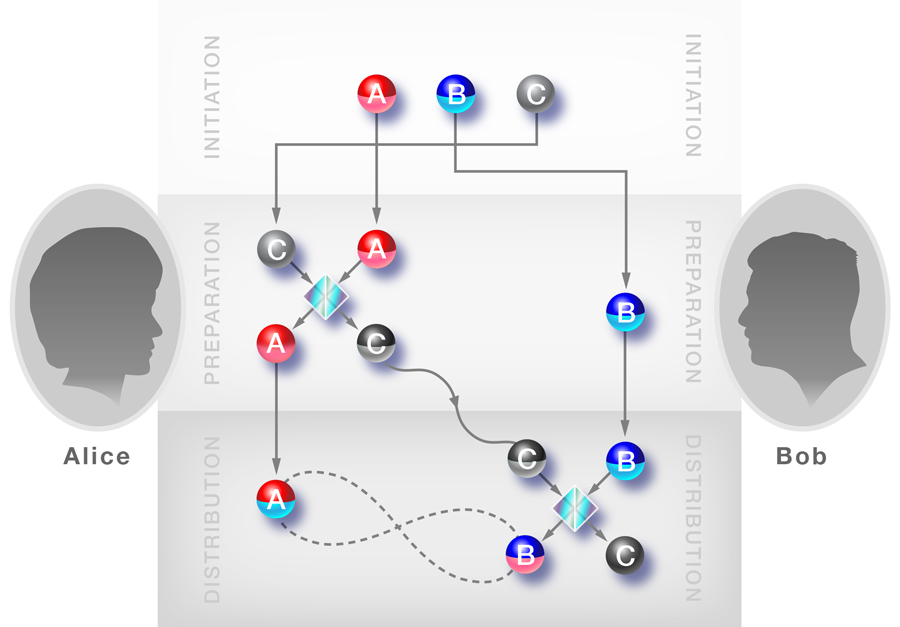
Following the general idea of Cubitt et al.’s original paper, Alessandro Fedrizzi from the University of Queensland, Australia, and co-workers have realized an experiment demonstrating the proposed entanglement distribution with separable carriers using polarization-encoded single photon states [2]. Their experiment illustrates quite nicely the crux of this strange type of entanglement distribution. The authors actually start with an entangled pair of photons, $A$ and $B$ , which are shared between Alice and Bob. However, they subsequently destroy this entanglement by randomly mixing the four different types of possible entangled states, the so-called Bell states. This procedure effectively prepares a separable mixed state between photons $A$ and $B$ , which nevertheless remains in a very specific form, carrying quite distinct correlations. The information carrier, photon $C$ , is prepared in a similar way, yielding, again, a specific mixed state.

Once all the photons are prepared, photons $A$ and $C$ pass through a quantum gate, which is implemented by some sort of quantum interference between them (see Fig. 1). Altogether this procedure produces a very particular three-party state, which is specifically tailored for the needs of the experiment. It has the remarkable property that we do not find any entanglement if we analyze the correlations between photon $C$ and a subsystem made of photons $A$ and $B$ . The same is true if we analyze photon $B$ with respect to photons $A$ and $C$ . Yet we do get measurable entanglement between photon $A$ and the subsystem of photons $B$ and $C$ . Thus sending photon $C$ from Alice to Bob communicates entanglement, though it is never entangled itself with the others.

Apart from gaining new insights into the fundamentals of quantum physics, one might ask about the benefits of the presented protocol over the direct transmission of the entangled photon pairs. As stated by the authors, there is no advantage if Alice and Bob have a maximally entangled state at their disposal. However, if the photon source is noisy, such entangled states are hard to produce, whereas Fedrizzi et al. show that the information carried by a separable photon would be more resilient against noise in some cases.

Although simple to imagine, single photons acting as binary qubits are difficult to prepare and to work with. A possible simplification is to translate the original protocol into the framework of Gaussian states, as recently proposed in [10]. Here the information is encoded on many photons using the Heisenberg uncertainty relation between the amplitude and phase of optical beams. This enables a simpler preparation of more flexible three-party states as well as an easy recombination of the final state into a true two-party (bipartite) system. Following up on this proposal, two groups—Christian Peuntinger of the Max Planck Institute for the Science of Light, Germany, and co-workers [3] and Christina Vollmer from the Albert Einstein Institute, Germany, and collaborators [4]—have implemented experiments, which establish entanglement by a separable state between two final light beams located at Alice’s and Bob’s stations.

In the first case, Peuntinger et al. start with three independent beams, where $A$ and $C$ are squeezed states with reduced uncertainty in amplitude or phase, and $B$ is the vacuum field. For the preparation of a correlated state between the beams, all three beams are manipulated with small displacements in amplitude or phase, or in both. These displacements are coordinated using a classical communication channel (i.e., LOCC). Once prepared, Alice interferes beams $A$ and $C$ using a beam splitter, and she then sends the resulting $C$ beam to Bob, who interferes it with his beam $B$ in another beam splitter (see Fig. 1). Throughout the protocol, beam $C$ remains separable from the other beams, but at the end, beams $A$ and $B$ share true bipartite entanglement.

In this way, Peuntinger et al. have realized a protocol with the special feature that it combines a quantum channel with classical communication between Alice and Bob. Surprisingly, Bob can even get entanglement a posteriori, by performing the classically communicated manipulations on beam $B$ after it has interfered with beam $C$ in the beam splitter. This highlights interplay between classical and quantum correlations and the role of separable states as quantum carriers.

Vollmer and co-workers use a very similar system with the same operating principle as the one just described. The main difference is that the initial state is not directly prepared by LOCC. The team starts with an entangled state and “hides” the entanglement by mixing one part of the system with a noisy thermal state. In their analysis, they investigate which features are needed to see the wanted effects. This reveals that only a specific class of entangled Gaussian states can be used for the preparation of the strange three-party state. Here, it is important that one starts with not very clean—this means mixed—quantum states, but the actual squeezing of the initial states, which is the more apparent quantum property, is less relevant.

In summary, all three experiments highlight that quantum communication really becomes more subtle if we use more than two photons or beams to create multimode states. This is particularly interesting if we extend quantum communication beyond two parties and into more complex quantum network structures. The experiments also provide a test bed for studying the interplay of entanglement, noise, and classical communication. Future work in this area should give a deeper understanding of the advantages of using separable states for entanglement distribution between Alice and Bob, as well as in more complex network structures.

References

A. Einstein, B. Podolsky, and N. Rosen, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?” Phys. Rev. 47, 777 (1935)
A. Fedrizzi, M. Zuppardo, G. G. Gillett, M. A. Broome, M. P. Almeida, M. Paternostro, A. G. White, and T. Paterek, “Experimental Distribution of Entanglement with Separable Carriers,” Phys. Rev. Lett. 111, 230504 (2013)
C. Peuntinger, V. Chille, L. Mišta, N. Korolkova, M. Förtsch, J. Korger, C. Marquardt, and G. Leuchs, “Distributing Entanglement with Separable States,” Phys. Rev. Lett. 111, 230506 (2013)
C. E. Vollmer, D. Schulze, T. Eberle, V. Händchen, J. Fiurášek, and R. Schnabel, “Experimental Entanglement Distribution by Separable States,” Phys. Rev. Lett. 111, 230505 (2013)
R. F. Werner, “Quantum States with Einstein-Podolsky-Rosen Correlations Admitting a Hidden-Variable Model,” Phys. Rev. A 40, 4277 (1989)
C. H. Bennett, D. P. DiVincenzo, J. A. Smolin, and W. K. Wootters, “Mixed-state Entanglement And Quantum Error Correction,” Phys. Rev. A 54, 3824 (1996)
T. S. Cubitt, F. Verstraete, W. Dür, and J. I. Cirac, “Separable States Can Be Used To Distribute Entanglement,” Phys. Rev. Lett. 91, 037902 (2003)
A. Steltsov, H. Kampermann, and D. Bruß, “Quantum Cost for Sending Entanglement,” Phys. Rev. Lett. 108, 250501 (2012)
T. K. Chuan, J. Maillard, K. Modi, T. Paterek, M. Paternostro, and M. Piani, “Quantum Discord Bounds the Amount of Distributed Entanglement,” Phys. Rev. Lett. 109, 070501 (2012)
L. Mišta, Jr. and N. Korolkova, “Distribution of Continuous-Variable Entanglement by Separable Gaussian States,” Phys. Rev A 77, 050302 (2008)

About the Author

Christine Silberhorn is a professor at the University of Paderborn, where she is leading a research group in the area of integrated quantum optics. Her interests cover novel optical technologies based on quantum optics, and light-based quantum systems for use in quantum communication and quantum information processing. She has contributed to the development of engineered quantum light sources using integrated optics and ultrafast pulsed lasers, the implementation of multichannel quantum networks for photon counting and quantum simulations, and the realization of quantum communication systems with bright light. She received her doctorate from the University of Erlangen in 2003, and worked as a postdoc at the University of Oxford from 2003 to 2004. From 2005 to 2010 she was a Max Planck Research Group Leader in Erlangen. (Photo by DFG Ausserhofer.)