Atomic Interactions at a Distance

Matthias Weidemüller

Viewpoint

Atomic Interactions at a Distance

Physics Institute, University of Heidelberg, 69120 Heidelberg, Germany

June 24, 2013• Physics 6, 71

A new experimental scheme uncovers the strength of the van der Waals force between two individual atoms and its dependence on the interatomic distance

Figure caption — **Figure 1:** Mapping out the van der Waals interaction between two atoms. (a) In the experiment of Béguin *et al.* two atoms are trapped in the foci of two laser beams separated by a distance $R$ . (b) Depending on $R$ , the excitation laser field can couple the ground state $| g g 〉$ of the atomic pair to states containing one atom in the Rydberg state ( $| g r 〉$ and $| r g 〉$ , respectively), or to a state with both atoms populating the Rydberg state $| r r 〉$ . The energy of the latter state is strongly shifted because of the van der Waals interaction $U_{v d W}$ between the atoms (see level diagram in the upper left), resulting in a distance-dependent coherent excitation dynamics of the atomic pair system. (c) By analyzing the time evolution of the atom-pair state, Béguin *et al.* deduce the van der Waals energy shift as a function of interatomic distance for different Rydberg states.

Van der Waals (vdW) forces are the dominant interactions between neutral particles on nanometer-to-micrometer length scales. This makes their effects ubiquitous in physics, chemistry, and biology: they are, for instance, responsible for the action of detergents, the self-assembly of viruses, and even the ability of geckos to climb flat surfaces. Their existence was first proposed by Johannes Diderik van der Waals in the late $19$ th century, as he developed an equation of state for gases and liquids that captures the gas-liquid transition and approximates the behavior of the liquid state. To derive his equation, van der Waals modified the ideal gas law by including an attractive interaction between molecules proportional to the inverse square of the gas volume, which suggested that the effective force between two neutral particles scales with their distance $R$ as $1 / R^{6}$ .

The importance of the vdW force has driven a long history of scientific investigations on its microscopic origin and its relation to macroscopic effects [1]. The internal structure of atoms and molecules as well as retardation effects (due to the fact that the interaction is mediated by photons, which have finite speed) can vastly alter the actual dependence of the intermolecular forces from the ideal $1 / R^{6}$ law. Yet for a long time it seemed practically impossible to directly probe the fundamental vdW interaction on the atomic scale: the vdW interaction energy between two atoms in the ground state is too small to be directly detected [at a distance of $1$ micrometers ( $μ m$ ), it would correspond to a thermal energy in the $10^{- 18}$ kelvin range]. Some information on its nanometer-range behavior has only been derived indirectly, by precision vibrational spectroscopy of diatomic molecules [2]. As reported in Physical Review Letters, Lucas Béguin at the French National Center for Scientific Research (CNRS) in Palaiseau, France, and co-workers, have now developed an elegant method capable of measuring, on micrometer scales, the strength of the vdW force between two individual atoms and its dependence on the interatomic distance [3].

The key idea behind the authors’ work is to use Rydberg atoms, instead of ground-state atoms, to enhance vdW interactions and make them measurable at macroscopic length scales. Rydberg atoms are atoms in which at least one electron is in a highly excited state (with large principal quantum number $n$ ). Since vdW interactions between atoms depend on their polarizability (which in the case of almost hydrogenlike Rydberg atoms scales as $n^{7}$ ), one can show that vdW forces scale as $n^{11}$ . The use of Rydberg atoms with $n$ in the $50$ – $100$ range can thus enhance the interaction energy by $17$ to $20$ orders of magnitude [4]. In the early 1990s, Ed Hinds, Serge Haroche, and co-workers used this favorable scaling to determine the strength of the vdW interaction between a Rydberg atom and its mirror image at a conducting surface [5]. More recently, measurement of collision dynamics of ultracold Rydberg atoms yielded a rough estimate of the vdW interaction strength between two Rydberg atoms at micrometer distances, but could not deliver conclusive information on the distance dependence, because of the random distribution of interatomic spacing in the gas [6].

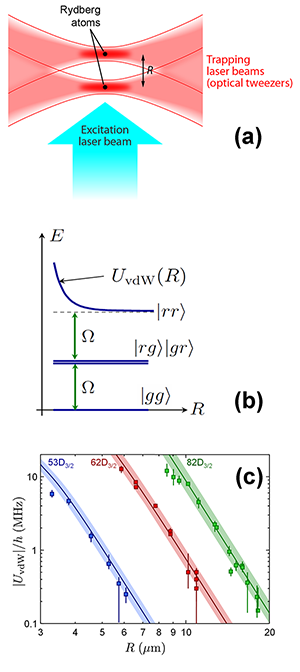
To measure the vdW interaction between two Rydberg atoms, one first needs to control the distance between the two atoms with micrometer accuracy. This can be accomplished by controlling the positions of the individual atoms with optical tweezers: dipole traps formed by tightly focused laser beams [7]. Béguin and co-workers confined single atoms in the foci of two tweezers whose distance could be precisely controlled, as shown in Fig. 1(a). They then measured the strength of the vdW interaction by monitoring its influence on the coherent evolution of a quantum-mechanical state of the atomic pair. The state is generated by coupling the (noninteracting) atomic ground state to the (strongly interacting) Rydberg state with a quasiresonant laser field.

The laser interaction makes the atoms go through Rabi oscillations between ground and excited states [see Fig. 1(b)]. Three oscillatory regimes can be identified, depending on the distance between the atoms. If the atoms are too far apart, the vdW interaction has no effect: both atoms independently oscillate with the Rabi frequency determined by the intensity of the laser field and its detuning from the atomic resonance. If they are too close, at most, the excitation of one Rydberg atom can be achieved (single Rydberg excitations): the Rabi frequency is smaller than the vdW induced frequency shift and the presence of one Rydberg atom shifts the second out of resonance (a phenomenon known as “vdW blockade”) [8]. Within the blockade radius, the pair of atoms undergoes a collective Rabi oscillation between the ground state and an entangled two-atom state containing only a single Rydberg excitation. [9]. In both limiting cases, the details of the Rabi oscillations do not provide direct information about the actual strength of the vdW interaction.

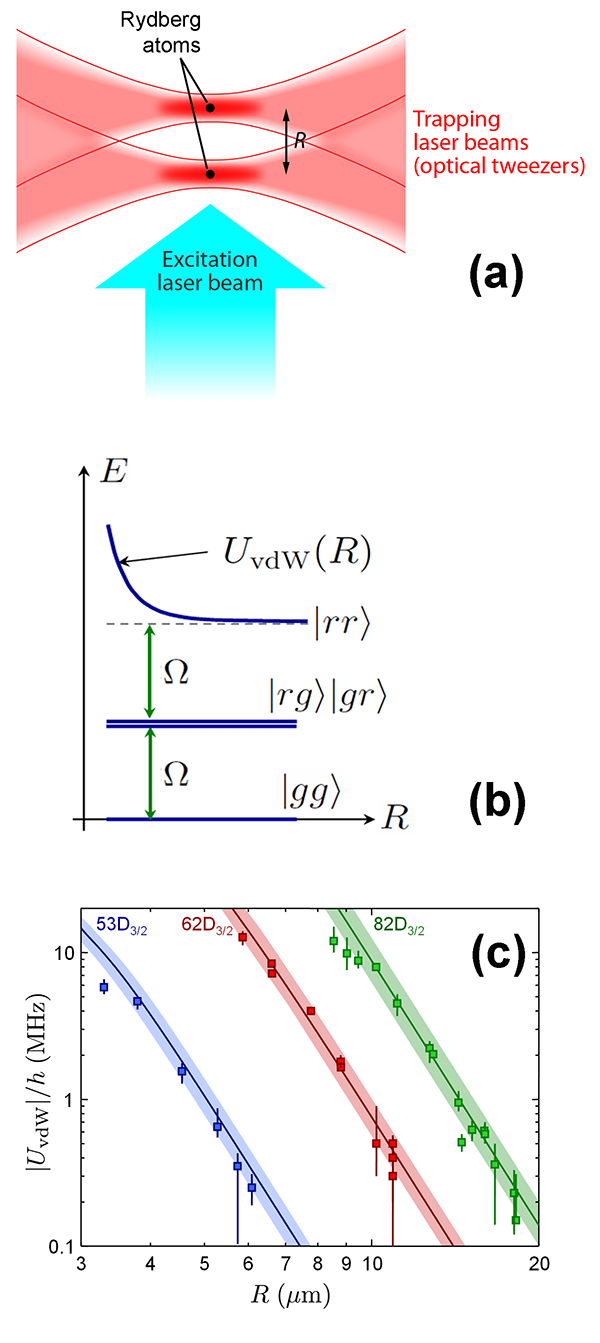
Béguin and colleagues realized that in the intermediate regime (for distances in the $1$ – $20$ $μ m$ range, depending on $n$ ) the coherent population dynamics of the atomic pair reveals accurate information on the vdW interaction: when Rabi frequencies are on the same order as the vdW frequency shift, the laser coherently couples the ground state to an excited atom-pair state, containing double Rydberg excitation. Since the energy of the latter state is strongly shifted because of the van der Waals interaction between the atoms [see Fig. 1(b)], the amplitude and frequency of the coherent wave packet motion are sensitively dependent on the strength of the vdW force. The authors mapped out the probability of finding single and double Rydberg excitations as a function of laser illumination time for different distances and Rabi frequencies. From this they could determine the vdW interaction strength as a function of distance. Their results, shown in Fig. 1(c), are consistent with a $1 / R^{6}$ dependence of a repulsive vdW force in the range between $3$ and $20$ $μ m$ for Rydberg states with principal quantum numbers between $n = 53$ and $82$ . The measured strength of the vdW interaction confirms predictions based on atomic structure calculations.

The measurement principle introduced by Béguin and colleagues has the potential to reveal fine details of the vdW interaction, such as the $R$ dependence over a wider range of distances, higher-order multipole contributions, and retardation effects due to quantum electrodynamic corrections. In fact, an obvious deviation from the simple $n^{11}$ scaling of the vdW force is already apparent in their data, caused by Förster resonances (level crossings of atomic pair states). Such resonances result in a significant modification of the interaction strength and a crossover from a vdW force to a resonant dipole force featuring a $1 / R^{3}$ dependence at shorter range [8].

It is also worth noting that the atomic pair states created by Béguin and colleagues are highly quantum entangled [9]. Having mastered the entanglement of an atom pair, one may now proceed to larger ensembles of well-localized atoms, thus opening the perspective of generating massively entangled many-atom states via the tunable vdW interaction. Such states may realize essential and long-sought-after elements in quantum computing schemes.

References

D. Langbein, Theory of van der Waals Attraction (Springer, New York, 1974)[Amazon][WorldCat]
C. Chin, R. Grimm, P. Julienne, and E. Tiesinga, “Feshbach Resonances in Ultracold Gases,” Rev. Mod. Phys. 82, 1225 (2010)
L. Béguin, A. Vernier, R. Chicireanu, T. Lahaye, and A. Browaeys, “Direct Measurement of the van der Waals Interaction between Two Rydberg Atoms,” Phys. Rev. Lett. 110, 263201 (2013)
T. F. Gallagher, Rydberg Atoms (Cambridge University Press, Cambridge, 1994)[Amazon][WorldCat]
V. Sandoghdar, C. I. Sukenik, E. A. Hinds, and S. Haroche, “Direct Measurement of the van der Waals Interaction between an Atom and Its Images in a Micron-Sized Cavity,” Phys. Rev. Lett. 68, 3432 (1992)
T. Amthor, M. Reetz-Lamour, S. Westermann, J. Denskat, and M. Weidemüller, “Mechanical Effect of van der Waals Interactions Observed in Real Time in an Ultracold Rydberg Gas,” Phys. Rev. Lett. 98, 023004 (2007)
R. Grimm, M. Weidemüller, and Y. B. Ovchinnikov, Optical Dipole Traps for Neutral Atoms, in Advances in Atomic, Molecular, and Optical Physics (Academic Press, San Diego, 2000), Vol. 42, p. 95[Amazon][WorldCat]
M. Saffman, T. G. Walker, and K. Mølmer, “Quantum Information with Rydberg Atoms,” Rev. Mod. Phys. 82, 2313 (2010)
E. Urban, T. A. Johnson, T. Henage, L. Isenhower, D. D. Yavuz, T. G. Walker, and M. Saffman, “Observation of Rydberg Blockade between Two Atoms,” Nature Phys. 5, 110 (2009); A. Gaëtan, Y. Miroshnychenko, T. Wilk, A. Chotia, M. Viteau, D. Comparat, P. Pillet, A. Browaeys, and P. Grangier, “Observation of Collective Excitation of Two Individual Atoms in the Rydberg Blockade Regime,” Nature Phys. 5, 115 (2009)

About the Author

Matthias Weidemüller holds a Chair for Experimental Physics at the Physics Institute of the University of Heidelberg and is Director of the Heidelberg Center for Quantum Dynamics. His research focuses on atomic and molecular quantum systems at different levels of complexity. The systems under investigation range from highly excited Rydberg atoms over atomic and molecular quantum gases to molecular aggregates. For more information visit http://www.physi.uni-heidelberg.de/Forschung/QD/.