Pushing on a Nonlinear Material
Understanding how materials bend, stretch, or compress under an applied force (or “load”) is essential in the design of buildings, vehicles, and machines. These deformations can be straightforwardly calculated for materials like aluminum, glass, or carbon fiber, which tend to deform little and can therefore, to a good approximation, be treated as linear: doubling the load doubles the effect, like pulling on a spring. In contrast, scientists are still looking for the right way to perform the equivalent calculations on stretchy materials like rubbers and foams, and disconnected “granular” materials, such as soil, sand, and cereals. All of these materials share a common property that they are easy to deform by large amounts, and therefore, the linear approximation no longer applies.
Corentin Coulais, now at the University of Leiden, the Netherlands, and his colleagues report experiments on a model “soil” in which they carefully tracked the soil’s elastic response to a force exerted on it via a series of very gradual steps [1]. By comparing their results to predictions of an idealized theory of granular materials, they were able to identify the theory’s strengths and limitations. The work could therefore help researchers develop more reliable methods for predicting the behavior of granular materials.
Physicists have been working on a number of models to understand how granular materials cross the boundary between being able to support a load to failing completely—a problem of considerable importance for engineers who need to know if a soil can serve as a foundation for a house or bridge. A promising route is to describe this boundary as a “jamming transition” [2,3]. In this picture, particles are collectively “jammed” into place by their neighbors. However, under an applied stress, they can dislodge from those cages and give way—an “unjamming” transition that is analogous to the melting of an ordinary solid. Similar to the thermodynamic equations of state, where compressibility is a known function of state variables like pressure or temperature, the theory behind jamming can predict material properties of granular materials, such as how they stiffen as a function of particle packing density. But, so far, most of these predictions assume that the particles are frictionless, leaving it unclear which aspects of the theory apply to real situations in which friction is present.
Coulais and his colleagues focused their study on two key predictions from the jamming framework [2,3] that had not been tested for real, frictional particles. The first is the values of the critical exponents that describe how elasticity and dilatancy (the tendency to decrease packing density under shear [4]) vary as the material is sheared near the jamming transition. The second is to measure how characteristic lengths, in this case the one that characterizes the onset of nonlinearity as a function of distance from a disturbance, depend on the proximity of the material to the jamming/unjamming transition.
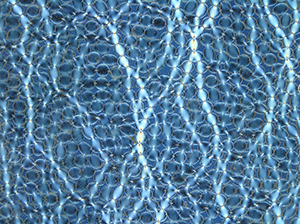
To test these predictions, they used an experimental technique that allowed them to measure the force on each particle as they pushed grains in a jammed state outward from the center of the material. Instead of actual grains of sand, they used 5-millimeter-diameter polymer disks, laying of these disks in a single, densely packed layer. The polymer disks are photoelastic, meaning they rotate the polarization of light passing through them by an amount that depends on how much stress they experience. When properly calibrated [5,6], these patterns of birefringence (Fig. 1) can measure the force at each individual contact.
To generate shear within the layer of disks, Coulais and his colleagues slowly inflated a 26-millimeter “balloon” at the center of the packed layer. They then observed the progressive changes in the particle-scale stress, strain, dilation, and pressure resulting from each inflation step. For the tiniest steps possible, the researchers observed that the grain-scale stresses (forces between particles) were a nonlinear function of the local strain (the amount the aggregate deformed). But with each subsequent step, the packing experienced a dilatancy-associated pressure rise and a decreased in stiffness. This dilatancy softening matches behavior predicted for frictionless particles and is consistent with jamming theory [7]. Interestingly, the material eventually crossed back into a regime that would seem to be linear, in the sense that double the deformation takes double the force. But the authors identified this regime as faux-linear, because it was full of microscopic nonlinearities that added up to a macroscopic linear response.
Finally, the authors examined the distance from the balloon at which the faux-linear regime transitions into truly nonlinear behavior. This distance was observed to be larger and larger as the aggregate approached the boundary between being jammed and unjammed. (In the experiments, the particles were always on the jammed side of this transition.) There have been theoretical predictions of a characteristic length scale near the jamming transition [2,3,8], but the scaling exponent observed here does not match these predictions. Understanding this new exponent thus poses a new theoretical challenge.
Researchers studying jamming have debated the question of how close to the jamming transition a granular material has to be in order to remain linear. So far, few experimental approaches could weigh in on the debate because linear behavior can only be seen within a small window of near-zero force—something hard to achieve experimentally. Direct measurements, such as these, are very important for settling this debate. The observed faux-linear regime is also a caveat to experimentalists: measuring a linear response does not mean that the system is in the original linear regime.
In many ways, the experiments from Coulais and his colleagues are still an abstraction of the real problem that the engineer faces: How much load can a soil embankment take before it enters the nonlinear regime, and then ultimately fails? To answer this question, the community is still waiting for experiments on, and the theory to describe, noncircular, nonuniform, three-dimensional particles.
This research is published in Physical Review Letters
References
- C. Coulais, A. Seguin, and O. Dauchot, “Shear Modulus and Dilatancy Softening in Granular Packings above Jamming,” Phys. Rev. Lett. 113, 198001 (2014)
- A. J. Liu and S. R. Nagel, “The Jamming Transition and the Marginally Jammed Solid,” Annu. Rev. Cond. Mat. Phys. 1, 347 (2010)
- M. Van Hecke, “Jamming of Soft Particles: Geometry, Mechanics, Scaling and Isostaticity,” J. Phys.: Condens. Matter 22, 33101 (2010)
- O. Reynolds, “On the Dilatancy of Media Composed of Rigid Particles in Contact,” Philosophical Magazine 20, 469 (1885)
- T. S. Majmudar and R. P. Behringer, “Contact Force Measurements and Stress-Induced Anisotropy in Granular Materials,” Nature 435, 1079 (2005)
- J. G. Puckett and K. E. Daniels, “Equilibrating Temperaturelike Variables in Jammed Granular Subsystems,” Phys. Rev. Lett. 110, 058001 (2013)
- B. Tighe, “Shear Dilatancy in Marginal Solids,” Granular Matter 16, 203 (2014)
- G. During, E. Lerner, and M. Wyart, “Phonon Gap and Localization Lengths in Floppy Materials,” Soft Matter 9, 146 (2013)