Time Trials for Fundamental Constants

Marianna S. Safronova

Viewpoint

Time Trials for Fundamental Constants

University of Delaware, Newark, DE 19716, USA
Joint Quantum Institute, NIST and the University of Maryland, College Park, MD 20899, USA

November 17, 2014• Physics 7, 117

Single-ion clocks yield new limits on how much the proton-to-electron mass ratio and the fine structure constant change over time.

Figure caption — **Figure 1:** Schematic experimental arrangement for measuring the “ $E 2$ ” and “ $E 3$ ” clock frequencies of a single $^{171} {Yb}^{+}$ ion. The $E 3 / E 2$ frequency ratio was determined by stabilizing one laser to the $E 3$ transition and the other laser to the $E 2$ transition and measuring the ratio between the laser frequencies with an optical frequency comb. (For experimental reasons, the researchers used infrared lasers that have to be frequency doubled to excite the $E 2$ and $E 3$ optical transitions.)

Theories aimed at unifying gravity with the three other fundamental forces (electromagnetic, weak, and strong) predict that certain fundamental constants could change in an expanding Universe [1]. Support for this possibility is mixed: Absorption spectra of interstellar matter have led to claims both for and against variations of the fine structure constant, $α = e^{2} / ħ c$ , and the proton-to-electron mass ratio, $μ = m_{p} / m_{e}$ [1–3]). In 2011, a large study of atomic transitions from distant quasars, combined with earlier observations, suggested $α$ was higher or lower depending on where one looked in the sky, with a significance of $4.2$ standard deviations [2]. Evidence that fundamental constants vary over time and space would imply that the laws of physics aren’t the same in all parts of the Universe, or at all times, an incredible possibility that needs to be tested with different experimental approaches. Now, two independent research groups, led by Patrick Gill at the National Physical Laboratory (NPL), UK, and Ekkehard Peik at the Physikalisch-Technische Bundesanstalt (PTB), Germany’s national metrology institute, have put new constraints on the possible time variation of the fine structure constant and the proton-electron mass ratio using high-precision atomic clocks based on a single ytterbium ion, $^{171} {Yb}^{+}$ [4,5]. Their work also lays the groundwork for using $^{171} {Yb}^{+}$ as an optical frequency standard that could potentially replace the current cesium frequency standard.

The frequencies of all atomic transition lines depend on some functional form of the fine structure constant. For example, relativistic corrections are proportional to $Z^{2} α^{2}$ , where $Z$ is the nuclear charge. The sensitivity to the proton-to-electron mass ratio is found in specific transitions between hyperfine states of atoms. These transitions, which typically lie in the microwave, depend on the ratio of the electron ( $μ_{B}$ ) and nuclear ( $μ_{N}$ ) magnetic moments and, therefore, $μ$ . Since $μ$ doesn’t contribute to the ratio of two optical transitions, comparing different optical transitions provides the cleanest measurement of $α$ variation. (Moreover, such comparisons eliminate the need to reference the cesium standard, a microwave transition with a relative uncertainty of order $10^{- 16}$ .) But a measurement of $μ$ variation, from comparing an optical transition to a microwave one, is necessarily always entangled with $α$ variation.

Astrophysical observations determine shifts in $α$ and $μ$ by comparing the spectra of light from $3$ to $10$ billion years ago to that from current laboratory measurements. In contrast, in an atom clock measurement of $α$ or $μ$ shifts the frequencies of two atomic transition lines—either on the same atom or on different atoms—are compared over time. So far, the most precise laboratory test of $α$ comes from NIST [6]. In these experiments, scientists measured the ratio of optical frequencies from ${Al}^{+}$ and ${Hg}^{+}$ ions, providing a limit on the time variation in $α$ to $- 1.6 \pm 2.3 \times 10^{- 17}$ per year.

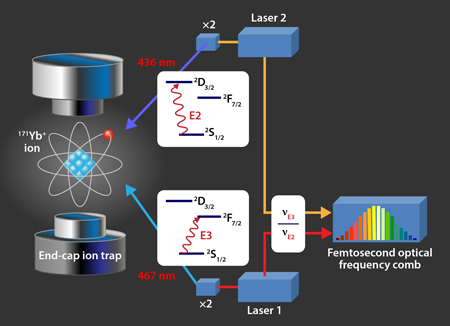
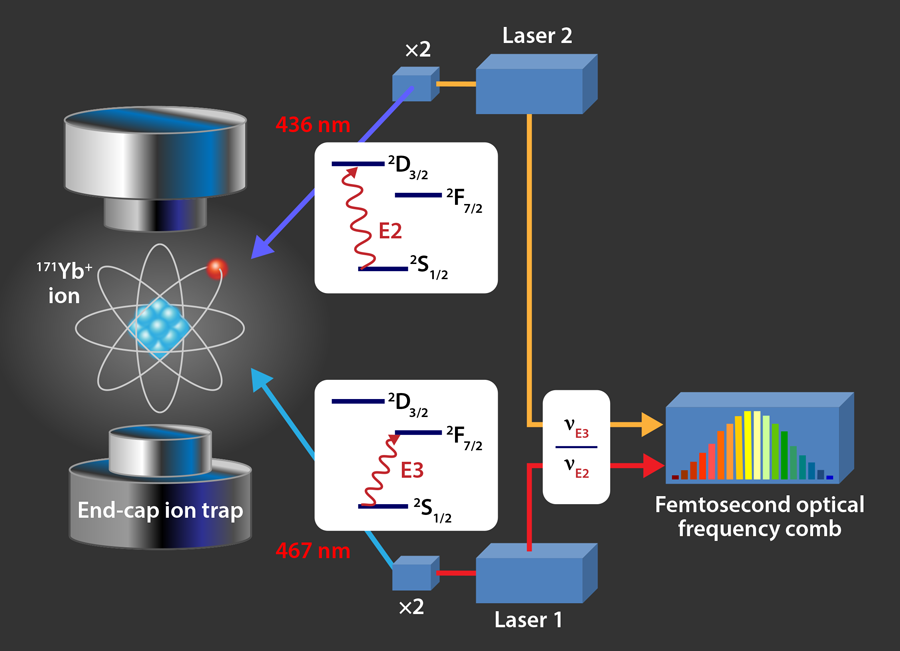
$^{171} {Yb}^{+}$ is a unique candidate for new tests of fundamental constants because it possesses two stable transition lines that can be measured from the same single ion and compared to each other, thus eliminating some systematic uncertainties that are common to both transitions. One transition on $^{171} {Yb}^{+}$ , called $E 3$ , is an electric-octupole transition at $467$ nanometers from the ground state to the first excited state, $^{2} S_{1 / 2}$ to $^{2} F_{7 / 2}$ , The other, called $E 2$ , is an electric-quadrupole transition from the ground state to the second excited state, $^{2} S_{1 / 2}$ to $^{2} D_{3 / 2}$ . The $E 3$ transition is particularly attractive as a frequency standard because quantum-mechanical selection rules prohibit all other faster transitions from the $^{2} F_{7 / 2}$ state to the ground state. The excited state can live on the order of years, giving the transition an extremely narrow linewidth that can be measured with high precision.

Theoretical calculations can predict how a particular transition frequency depends on $α$ . And the more sensitive a certain transition is to $α$ variation, the better the limit that can be set with a precise measure of the transition frequency. For the purposes of measuring shifts in the fine structure constant, ${Yb}^{+}$ has two advantages. First, it has a large nuclear charge ( $Z = 70$ ), which enhances the relativistic effects that depend on $α$ . Second, the frequencies of the $E 2$ and $E 3$ transitions should shift in opposite directions for a given shift in $α$ , which enhances the net effect of the shift. (The $^{2} F_{7 / 2}$ and $^{2} D_{3 / 2}$ excited states have very different electronic configurations, which gives them a different $α$ dependence.)

Both the NPL [4] and PTB [5] groups devised their experiments to make systematic uncertainties (i.e., those coming from experimental error) in the measurement of the ${Yb}^{+}$ $E 2$ and $E 3$ frequencies as small as possible, and both have significantly improved the precision of the $E 3$ standard. The NPL researchers report the $E 3$ transition has a frequency $642$ $121$ $496$ $772$ $644.91$ with a relative uncertainty of $6 \times 10^{- 16}$ ; the PTB researchers report a value $642$ $121$ $496$ $772$ $645.36$ with a slightly lower relative uncertainty of $3.9 \times 10^{- 16}$ . By comparing their measured values of the $E 3$ transition in ${Yb}^{+}$ to the cesium frequency standard, they extracted limits on the time variation of $α$ and $μ$ , which, when combined with other measurements, yielded new constraints of $- 0.7 \pm 2.1 \times 10^{- 17}$ per year and $0.2 \pm 1.1 \times 10^{- 16}$ per year (NPL) and $- 0.20 \pm 20 \times 10^{- 16}$ per year and $- 0.5 \pm 1.6 \times 10^{- 16}$ per year (PTB). In particular, they improved constraints on the time variation of $μ$ by a factor of $2$ and $3$ (Ref. [4] and Ref. [5], respectively) over the previous best constraint, which was measured with a rubidium microwave clock [7]. These constraints are about a factor of $10$ tighter than astrophysical measurements of a time-varying $α$ , and they are consistent with astrophysical measurements of the time variation of $μ$ , which indicate any variation is less than $0.21 \times 10^{- 16}$ per year [3].

In addition to providing new constraints on the fundamental constants, the NPL group [4] carried out a direct measurement of the frequency ratio of $E 2$ and $E 3$ optical clock transitions in the same $^{171} {Yb}^{+}$ ion—the first time that two such transitions have been compared on the same ion. The scheme of this measurement is given in Fig. 1. Two clock transitions were measured simultaneously, which reduces systematic effects common to both transitions. The researchers stabilized one laser to the $E 3$ transition and one laser to the $E 2$ transition and used an optical frequency comb to read out, extremely precisely, the frequency on each laser. In the future, direct, repeated measurements of the $E 3 / E 2$ optical frequency ratio, free from the additional uncertainties that come from comparisons to the cesium standard, are expected to yield an even tighter constraint on the time variation of $α$ . Moreover, these transitions could be the basis of new, more precise frequency standards, which are essential for new tests of fundamental physics, very-long-baseline interferometry for telescope array synchronization, and the development of extremely sensitive quantum-based tools for geodesy, hydrology, tracking of deep-space probes, and other applications [8].

A measurement that showed a fundamental constant varies in time would be a clear signature of new physics—an exciting possibility. However, a null result, such as that reported by the NPL and PTB groups, is also of crucial importance: it gives us confidence that our measurement devices don’t depend on space or time—at least within the accuracy of current experiments. Moreover, the new system of units will be based on fundamental constants [9] so it is important to know if, and by how much, they could vary.

This research is published in Physical Review Letters.

References

J.-P. Uzan, “Varying Constants, Gravitation and Cosmology,” Living Rev. Relativity 14, (2011)
J. K. Webb, J. A. King, M. T. Murphy, V. V. Flambaum, R. F. Carswell, and M. B. Bainbridge, “Indications of a Spatial Variation of the Fine Structure Constant,” Phys. Rev. Lett. 107, 191101 (2011)
J. Bagdonaite, P. Jansen, C. Henkel, H. L. Bethlem, K. M. Menten, and W. Ubachs, “A Stringent Limit on a Drifting Proton-to-Electron Mass Ratio from Alcohol in the Early Universe,” Science 339, 46 (2012)
N. Huntemann, B. Lipphardt, Chr. Tamm, V. Gerginov, S. Weyers, and E. Peik, “Improved Limit on a Temporal Variation of $m_{p} / m_{e}$ from Comparisons of ${Yb}^{+}$ and Cs Atomic Clocks,” Phys. Rev. Lett. 113, 210802 (2014)
R. M. Godun, P. B. R. Nisbet-Jones, J. M. Jones, S. A. King, L. A. M. Johnson, H. S. Margolis, K. Szymaniec, S. N. Lea, K. Bongs, and P. Gill, “Frequency Ratio of Two Optical Clock Transitions in ${}^{171}{Yb}^{+}$ and Constraints on the Time Variation of Fundamental Constants,” Phys. Rev. Lett. 113, 210801 (2014)
T. Rosenband et al., “Frequency Ratio of Al+ and Hg+ Single-Ion Optical Clocks; Metrology at the 17th Decimal Place,” Science 319, 1808 (2008)
J. Guéna, M. Abgrall, D. Rovera, P. Rosenbusch, M. E. Tobar, Ph. Laurent, A. Clairon, and S. Bize, “Improved Tests of Local Position Invariance Using ${}^{87}{Rb}$ and ${}^{133}{Cs}$ Fountains,” Phys. Rev. Lett. 109, 080801 (2012)
N. Hinkley, J. A. Sherman, N. B. Phillips, M. Schioppo, N. D. Lemke, K. Beloy, M. Pizzocaro, C. W. Oates, and A. D. Ludlow, “An Atomic Clock with 10-18 Instability,” Science 341, 1215 (2013)
http://www.bipm.org/en/measurement-units/new-si/

About the Author

Marianna Safronova received her Ph.D. in physics from the University of Notre Dame in 2001 and joined NIST in 2001 as a guest researcher. In 2003, she accepted a faculty position at the University of Delaware in the Department of Physics and Astronomy. She is also an Adjunct Fellow at the Joint Quantum Institute, NIST and University of Maryland. Her research interests include the study of fundamental symmetries, atomic clocks, searches for the variation in fundamental constants, the study of long-range interactions, optical cooling and trapping of neutral atoms, and the development of high-precision methods for calculating atomic properties. She is a Fellow of the American Physical Society and a member of the Editorial board of the Physical Review A.