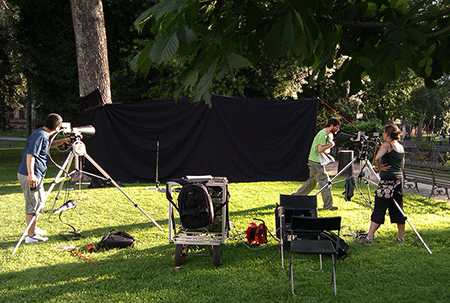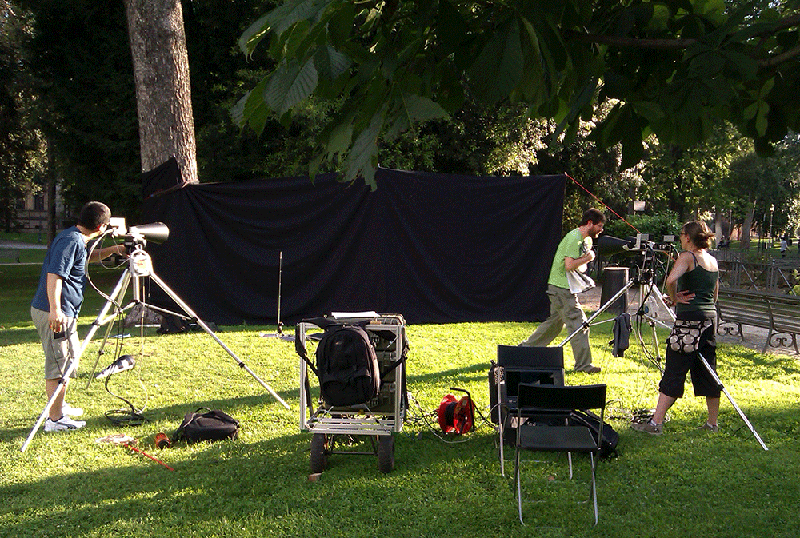Insect Swarms Go Critical
Scientists have found tantalizing evidence that diverse biological systems, including the human brain, gene expression networks, bird flocks, and fish schools, behave as though they are near the “critical point” of a phase transition, like correlated spins in a magnet on the verge of ordering. In flocks of starlings, for example, the velocity fluctuations of two distant birds mutually influence each other. Such “scale-free” correlations, which occur on all possible length scales in the flock, are a hallmark of criticality. The idea that biological systems could be described by the physics of phase transitions is exciting, as it could point to a common organizing principle in the evolution of seemingly different biological structures [1]. But direct evidence for this idea, which first emerged two decades ago [2,3], remains relatively scarce [4]. Now, a statistical study of insect swarms by Alessandro Attanasi and his colleagues at the University “La Sapienza” of Rome in Italy provides new evidence in support of this picture [5]. The researchers used video to track the trajectories of hundreds of swarming midges (a type of small fly commonly found in cities). By analyzing the statistical properties of trajectories in swarms of different sizes, they show that midges exhibit the same scale-free correlations as flocking starlings, and argue that the swarms appear to always be poised at a critical point.
In statistical physics, the critical point on a phase diagram often separates an ordered phase from a disordered phase. For a biological system, being at such a point could have certain advantages: If the system is too ordered, it cannot adapt or respond to change in its environment; if it is too disordered, the response may not be strong enough. At a critical point, a small action by one or a few individuals in the group, such as responding to a predator, can ripple to distant neighbors thanks to long-range correlations. But before scientists can think about how and why biological systems might have evolved to be critical, more evidence that this actually happens is needed.
In their new work, Attanasi and his colleagues set out to the parks of Rome to record high-speed videos of swarms of midges native to the area (Fig. 1). The movies, taken from three different viewpoints against a dark screen, were then processed to locate each midge and reconstruct its trajectory (Fig. 2). The largest dataset followed 600 midges flying for ten seconds.
Unlike graceful birds traveling in a flock, insects in a swarm tend to just hover over a spot on the ground (such as still water.) But the analysis of Attanasi et al. reveals that the seemingly disorganized swarms have some sophisticated features. For each swarm, the authors calculated, from the midge trajectories, the correlation length of velocity fluctuations, which they define as the characteristic distance beyond which midge-midge correlations decay below a given threshold. They define the average distance between nearest-neighbor midges as the “control parameter”—akin to temperature or pressure in a true phase transition, except that its value cannot be changed for a given swarm. They also calculate a susceptibility that, in qualitative terms, measures the total correlation between insects. Their analysis shows that the correlation length and the magnitude of the susceptibility grow with the number of insects in the swarm, while the spacing between midges decreases.
Attanasi et al. interpret their data using the so-called Vicsek model, which, in simple terms, attempts to model collective motion by assuming that an individual in a group essentially follows the trajectory of its neighbors, with some deviations modeled as “noise.” In this model, a phase transition from an ordered “flocking state” to a disordered one occurs when the noise rises above a certain level. Now, in theory, true criticality only occurs in infinite systems, a criterion effectively fulfilled by magnets and other solids, since the number of elements they contain are on the scale of Avogadro’s number. Biological groups, on the other hand, are typically much smaller, and their critical points are smeared out over an extended transition region. Attanasi et al. show that the variation with swarm size of the quantities they measure is, as expected in the Vicsek model for finite-size systems, sitting near the maximally correlated point of their transition region. In particular, midges seem to regulate their average distance—or, conversely, swarms regulate their population—so as to function at maximal possible criticality.
Attanasi et al.’s attractive message is that biological groups, such as swarms, coordinate their behavior so as to optimize the ability to react collectively (e.g., to avoid predators or to attract sexual partners). Their observations, in fact, provide stronger evidence in support of criticality in animal groups than the scale-free correlations found in more ordered groups like starling flocks: Because starlings “pick” a direction, they represent a system in which rotational symmetry has been broken, and in such systems, scale-free correlations occur even away from the critical point.
One weakness of Attanasi et al.’s data, however, is that they only allow comparisons of swarms that differ in number by an order of magnitude. This difference is too small to ensure the reported size effects are evidence of criticality. Larger groups will have to be analyzed in the future. A more controlled environment might help too, although recent laboratory experiments on swarms of fewer than 50 midges don’t indicate critical behavior [6], which may signal that it arises only in “natural conditions”.
The criticality hypothesis has gained considerable popularity and empirical support in the field of neuroscience [4,7]. Researchers have discovered critical-like neuronal avalanches and evidence that the background dynamics of the brain has features of criticality [7]. Similarly, empirical evidence suggests that genetic regulatory networks might also operate at criticality [8]. A “critical” brain could have several functional advantages, such as enhanced response to stimuli, the ability to exist in many states, and optimal transmission and storage of information [7]. Bolstering this idea, researchers have argued that complex computations can only be performed by “machines” operating at criticality [2,9].
In these examples and the work by Attanasi et al, however, we are left with the challenge of understanding how a biological system arrives and stays at criticality. While magnets only exhibit critical behavior at a very precise temperature, animal groups and neurons seem to operate generically near critical points. So why is critical behavior so ubiquitous in nature?
One popular proposal from the 1980s is “self-organized criticality” (SOC), a collection of simple models and mechanisms aimed at offering a common explanation for why earthquakes, avalanches of flux lines in superconductors and solar flares are generically scale invariant [10]. SOC models have been extended to biological systems, and not without reason: the critical avalanches observed in neuronal activity, for example, are reminiscent of earthquakes [10]. But the SOC picture isn’t entirely satisfactory because it ignores functional aspects of biological systems. An alternative, and more biologically centered, proposal [11] suggests living systems can, by virtue of their need to have both an accurate and flexible understanding of each other, adapt spontaneously towards a critical state. Criticality that emerges in this way may, at larger time scales, provide an optimal trade-off between robustness and evolvability.
It would be nice to see all the pieces of evidence crystalizing into a robust theory of criticality in biological systems. Extracting quantities like the order parameter, correlation lengths and susceptibilities from real systems is essential to point scientists towards the right model. As beautifully shown by Attanasi et al., unsuspecting midges could help a lot!
This research is published in Physical Review Letters and PLoS Computational Biology.
References
- M. T. Mora and W. Bialek, “Are Biological Systems Poised at Criticality?” J. Stat. Phys. 144, No. 2, 268 (2011); W. S. Bialek, “Biophysics: Searching for Principles,” (Princeton University Press, Princeton, 2012)[Amazon][WorldCat]
- S. Kauffman, “The Origins of Order: Self-organization and Selection in Evolution,” (Oxford University Press, New York, 1993)[Amazon][WorldCat]
- D. Chialvo, “Emergent Complex Neural Dynamics,” Nature Phys. 6, 744 (2010)
- A word of caution is that the control parameters that describe criticality are often inferred from mathematical models, and inferred models can have the misleading tendency to look critical when describing heterogeneous data. I. Mastromatteo and M Marsili, “On the Criticality of Inferred Models,” J. Stat. Mech. 2011, 10012 (2011)
- Alessandro Attanasi et al., “Finite-Size Scaling as a Way to Probe Near-Criticality in Natural Swarms,” Phys. Rev. Lett. 113, 238102 (2014); See also A. Attanasi et al., “Collective Behaviour without Collective Order in Wild Swarms of Midges,” PLoS Comp. Biol. 10, 7 (2014)
- J. G. Puckett and N. T. Ouellette, “Determining Asymptotically Large Population Sizes in Insect Swarms,” J. R. Soc. Interface 11, 20140710 (2014)
- H. G. Schuster in “Criticality in Neural Systems,” edited by Dietmar Plenz and Ernst Niebur (John Wiley and Sons, Weinheim, 2014)[Amazon][WorldCat]
- M. Nykter, N. D. Price, M. Aldana, S. A. Ramsey, S. A. Kauffman, L. Hood, O. Yli-Harja, and I. Shmulevich, “Gene Expression Dynamics in the Macrophage Exhibit Criticality,” Proc. Natl. Acad. Sci. U.S.A. 105, 1897 (2008)
- C. Langton, “Computation at the Edge of Chaos: Phase Transitions and Emergent Computation,” Physica D 42, 12 (1990)
- H. J. Jensen Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems (Cambridge University Press, New York, 1998), Vol. 10 [Amazon][WorldCat]; R. Dickman, M. A. Muñoz, A. Vespignani, and S. Zapperi, “Paths to Self-Organized Criticality,” Braz. J. Phys. 30, 27 (2000); J. A. Bonachela et al., “Self-Organization Without Conservation: Are Neuronal Avalanches Generically Critical?,” J. Stat. Mech. Theor. Exp. 2010, 02015 (2010)
- J. Hidalgo, J. Grilli, S. Suweis, M. A. Muñoz, J. R. Banavar, and A. Maritan, “Information-Based Fitness and the Emergence of Criticality in Living Systems,” Proc. Natl. Acad. Sci. U.S.A. 111, 10095 (2014)