Polarization that Holds Steady
Ferroelectrics are bistable materials, meaning that they can be in an electrically polarized state that is oriented either “up” or “down.” An electric field can switch the orientation of these states back and forth—a property that makes ferroelectrics useful as components in random access memories, in which the “up” or “down” state of the material encodes a or a data bit, respectively [1]. And since electric fields require less power to produce than the magnetic fields used in most magnetic storage memories, ferroelectric devices are attractive for a wide variety of applications.
Despite their technological appeal, however, ferroelectrics, particularly in the thin-film form most commonly needed for modern devices, are plagued by a common problem: the depolarization field—an internal electric field that competes with, and often destroys, ferroelectricity. Writing in Physical Review Letters, Kevin Garrity and his colleagues at Rutgers University, New Jersey, have now shown theoretically that a family of semiconductor materials predicted to be ferroelectric is also unusually resistant to the effects of the depolarization field [2]. These materials, which the authors have dubbed “hyperferroelectrics,” could be useful for making small-scale devices in which a ferroelectric thin film needs to be integrated with semiconducting components.
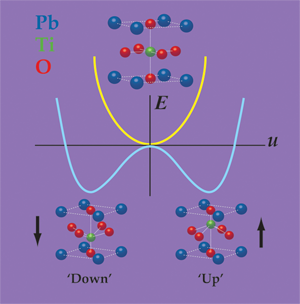
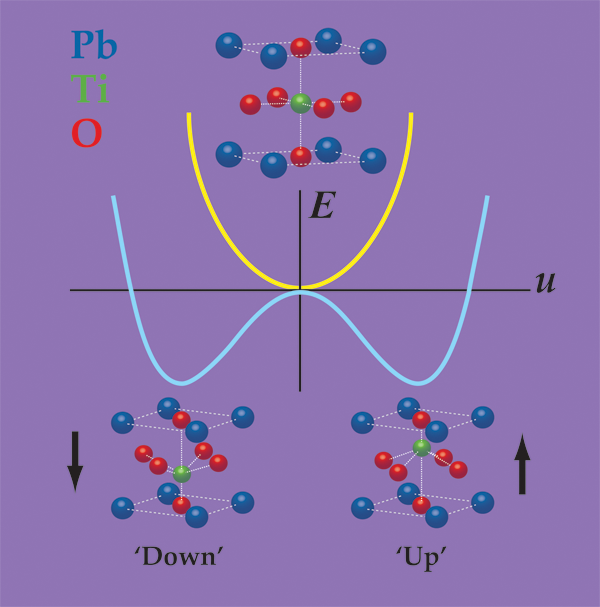
In a prototypical ferroelectric material, such as the perovskite oxide , ferroelectricity arises from the spontaneous displacement of the positively charged lead (Pb) and titanium (Ti) cations against the negatively charged oxygen anions. One can think of the ferroelectric distortion as originating from the bonding preferences of the Ti ion, which is slightly “too small” for its coordination cage. By moving slightly off-center, the Ti ion can achieve a better distribution of bond distances, and thus lower the energy of the material. (This picture is an oversimplification; in actuality, all of the atoms move and many forces contribute.) As shown in Fig. 1, the Ti ion can equivalently move towards the “top” or the “bottom” of the cage, thereby leading to the “up” and “down” states, either of which has a lower energy than the undistorted configuration.
Unfortunately, slabs of and many other ferroelectrics can’t spontaneously polarize in vacuum, or often, in air. The reason is that if all of the positive cations move in the same direction, then positive charge will accumulate on one surface and negative charge on the other. Gauss’s law tells us that these charges will produce a strong electric field that counteracts the displacement of the cations, essentially pushing them back into their positions in the nonferroelectric structure. The depolarization field has a large and positive electrostatic cost, which can overwhelm the energy gained through the ferroelectric distortion. In ferroelectric materials less than about nanometers in thickness, even a small residual depolarization field can completely suppress ferroelectricity [3,4].
One way to suppress the depolarization field is to sandwich the ferroelectric between short-circuited metallic electrodes, so that the free charges at the electrode surfaces exactly neutralize the polarization charges. In real devices, however, this screening can never be perfect and a residual depolarization field remains. In fact, the energetic cost of the depolarization field is so high that most known materials (with some exceptions [5–7], see 7 March 2011 Viewpoint) lose their ferroelectric properties unless the surface charges are perfectly screened, a requirement that is very difficult to satisfy in practice. In oxide ferroelectrics displaying the same kind of ferroelectric mechanism as , the depolarization field must be weakened by at least to allow a spontaneous polarization to arise [8].
But as Garrity and his colleagues point out, so-called hyperferroelectrics—a class of semiconductors that they predicted in 2012 to be ferroelectrics [9] (see 18 October 2012 Synopsis)—should maintain their polarization even in an unscreened depolarization field. Hyperferroelectrics have an stoichiometry ( and are all different elements) and a structure that can be described as “stuffed” wurtzite. Unlike the oxide ferroelectrics, in which the bonds between atoms are mostly ionic, hypeferroelectrics have atoms that are primarily covalently bonded.
Indeed, it is precisely this different bonding character that allows these materials to remain ferroelectric in the absence of screening. From a classical point of view, one can describe the ferroelectric polarization as a dipole per unit volume: , where is the “dynamical charge” carried by the ionic lattice along the distortion path, is the distortion amplitude and is the unit cell volume. The electrostatic energy of the depolarization field goes like (see Fig. 1), with a prefactor that is proportional to the square of , and inversely proportional to the electronic polarizability of the material. (This is in all respects analogous to the case of a two-plate capacitor: , where is the energy, the free charge, and the capacitance.) In semiconductors, the electronic orbitals are less tightly bound to the atomic nuclei than in perovskites, and so they have a higher electronic polarizability. Compared to perovskites, is also smaller in the materials. Both factors act to reduce the electrostatic cost of the depolarization field, such that it no longer outweighs the energy that can be gained from the ferroelectric distortion. (Although the dynamical charge is smaller for hyperferroelectrics, the magnitude of their polarization—the quantity that actually matters for applications—is just as large as in the best oxide ferroelectrics, such as .)
To demonstrate the unusual electrical characteristics of hyperferroelectrics, the authors calculated the properties of superlattices in which slabs of the hyperferroelectric material were sandwiched between insulating layers of nonferroelectric materials. In such a configuration, a normal ferroelectric wouldn’t polarize because there are no free charges to screen the depolarization field. Garrity et al., however, show that even a single layer of hyperferroelectric can polarize in this superlattice geometry. The authors speculate that the polarization, band gap, and other electrical properties could all be tailored for particular applications by adjusting the number of hyperferroelectric and nonferroelectric layers in these superlattices.
Hyperferroelectrics haven’t been studied experimentally, and some of the stoichiometries that Garrity et al. have predicted have yet to be synthesized. But their potential for applications is enticing. For one, as devices become increasingly smaller, ferroelectrics for memory storage or in capacitors are most likely to be needed in thin-film form. In addition, unlike most oxide ferroelectrics, which are insulators, hyperferrolectrics are semiconductors. Even though researchers have shown they can integrate ferroelectric oxides with silicon to create new kinds of electronic devices and components, such as ferroelectric field-effect transistors, the oxides are known to react with silicon and form phases that are deleterious to the electrical performance of the device. Hyperferroelectrics, in contrast, open up the possibility of making an all-semiconducting ferroelectric field-effect transistor, circumventing many of the materials issues that have hampered progress so far.
From a more general perspective, the work of Garrity et al. highlights the value of looking outside well-studied classes of compounds for new functional materials. Just when it appeared we had worked out the fundamentals of a material property, this new discovery adds to our understanding and creates new possibilities for practical applications.
References
- J. F. Scott and C. A. Paz De Araujo, “Ferroelectric Memories,” Science 246, 1400 (1989)
- Kevin F. Garrity, Karin M. Rabe, and David Vanderbilt, “Hyperferroelectrics: Proper Ferroelectrics with Persistent Polarization,” Phys. Rev. Lett. 112, 127601 (2014)
- J. Junquera and Ph. Ghosez, “Critical Thickness for Ferroelectricity in Perovskite Ultrathin Films,” Nature 422, 506 (2003)
- M. Stengel and N. A. Spaldin, “Origin of the Dielectric Dead Layer in Nanoscale Capacitors,” Nature 443, 679 (2006)
- N. Sai et al., “Absence of Critical Thickness in an Ultrathin Improper Ferroelectric Film,” Phys. Rev. Lett. 102, 107601 (2009)
- N. A. Benedek and C. J. Fennie, “Hybrid Improper Ferroelectricity: A Mechanism for Controllable Polarization-Magnetization Coupling,” Phys. Rev. Lett. 106, 107204 (2011)
- M. Stengel, C. J. Fennie, and Ph. Ghosez, “Electrical Properties of Improper Ferroelectrics from First Principles,” Phys. Rev. B 86, 094112 (2012)
- W. Zhong et al., “Giant LO-TO Splittings in Perovskite Ferroelectrics,” Phys. Rev. Lett. 72, 3618 (1994)
- J. W. Bennett, K. F. Garrity, K. M. Rabe, and D. Vanderbilt, “Hexagonal ABC Semiconductors as Ferroelectrics,” Phys. Rev. Lett. 109, 167602 (2012)