Quasiparticle Signatures in Quantum Spin Liquids

Alexei M. Tsvelik

Viewpoint

Quasiparticle Signatures in Quantum Spin Liquids

Brookhaven National Laboratory, Upton, NY 11972, USA

May 21, 2014• Physics 7, 54

The response of quantum spin liquids to an oscillating magnetic field should provide measurable signatures of Majorana fermions and other quasiparticles.

Figure caption — **Figure 1:** (a) Kitaev’s model describes a two-dimensional system of spins $S = 1 / 2$ on a honeycomb lattice interacting through a strongly anisotropic exchange interaction. Under certain conditions, the system is a quantum spin liquid (QSL), in which the spin arrangement is constantly in flux. (b) Phase diagram for a QSL. The model predicts a gapped and a gapless phase. The latter should host propagating Majorana fermions, whose signatures could be measured, according to the work of Knolle *et al.* [2]

Quantum spin liquids (QSLs) are systems of interacting spins that have a disordered ground state: while the materials are solid crystals, their spin arrangements are constantly in flux, much like the molecules of an ordinary liquid. There are several candidates for QSL, but their experimental observation remains controversial. QSLs are of great interest in their own right, but they may also serve as platforms for “topological quantum computing,” which may outperform conventional computing in carrying out certain algorithms [1].

From the theoretical point of view, the main difficulty is that QSLs are strongly correlated systems, in which mutual electronic interactions are not weak and single-electron approximations are inapplicable. This makes it difficult to carry out reliable calculations. Within this context, an exactly solvable QSL model found by Alexei Kitaev in 2006 [1] provided a gold standard. His solution described the system’s excitation spectrum and its thermodynamics but could not tackle the spin response functions, which describe how spins respond to a time-dependent magnetic field. Calculations of such functions turned out to be considerably more difficult. As reported in Physical Review Letters, Roderich Moessner and colleagues at the Max Planck Institute for the Physics of Complex Systems, Germany, together with John Chalker at the University of Oxford, UK, have now successfully tackled this problem [2]. The result offers a key advance in the theoretical understanding of QSLs and may be an important tool to guide experimental investigations. In particular, the authors identify measurable quantities associated with quasiparticles, crucial to QSL physics, including the elusive Majorana fermions—particles that are their own antiparticles, which were introduced by Ettore Majorana in 1937 in the context of particle physics but have not yet been observed.

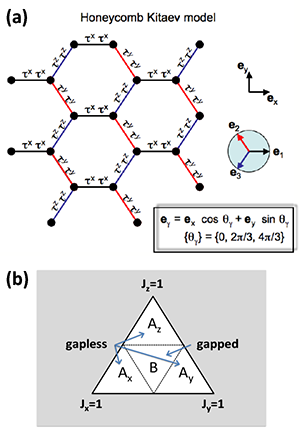
Moessner et al.’s work builds on Kitaev’s model, which describes a two-dimensional system of spins with $S = 1 / 2$ on a honeycomb lattice [see Fig. 1(a)] interacting through a strongly anisotropic exchange interaction—the purely quantum effect responsible, for instance, for ferromagnetism in some materials. Unlike the isotropic ferromagnetic case, Kitaev’s model posits an exchange along each link of the lattice that involves only one spin component ( $x$ component on $e_{1}$ , $y$ component on $e_{2}$ , and $z$ component on $e_{3}$ , as shown in Fig. 1). It has been suggested that such anisotropic exchange (hence the conditions for a QSL) may occur in certain transition metal compounds with strong spin-orbit coupling [3]. But it is likely that it is contaminated by the presence of the conventional isotropic exchange [4].

Kitaev’s model is only an approximation of real-world systems, but there are important reasons why it is of a great interest for theorists. First of all, there are few examples of models describing such complex systems that can be solved exactly, and having such simple solutions is almost miraculous. Second, the system properties revealed by this solution are quite unusual: It turns out that the system of interacting spins under consideration is a QSL. It never locks into an ordered state and its spin-spin correlations remain short range. Despite this lack of order, the phase diagram has a region where the excitation spectrum is gapless. As it turns out, particles in this region of the spectrum could be the solid-state equivalent of Majorana fermions.

In real space, the Majorana fermion is described by a real field that is equal to its Hermitian conjugate: $χ (r) = χ^{+} (r)$ . In momentum space, this means that the creation operator is equal to the annihilation operator with the opposite momentum: $χ (- k) = χ^{+} (k)$ . Hence Majorana fermions can be represented as a linear combination of creation and annihilation operators. This situation is analogous to a type of quasiparticle found in superconductors, called a Bogoliubov quasiparticle, which is also a linear combinations of a particle and antiparticle (holes).

In the context of the Kitaev model, such Majorana fermions emerge as collective degrees of freedom—the operator describing the fermion field at a given point is made up of all the spins of the system by means of a Jordan-Wigner transformation. Such transformations have been used primarily in one-dimensional systems where the fermions have a clear physical meaning, namely, domain walls between different ground states. In one dimension, the walls are pointlike objects that can propagate like particles. At first sight, this is not possible in higher dimensions, but the Kitaev model suggests a mechanism by which it could happen. It turns out that the Jordan-Wigner transformation converts the spin model into a model where, besides fermions, there is also a gauge field. This field (which is static in Kitaev’s model) creates landscapes in which Majorana fermions exist and can propagate in two dimensions.

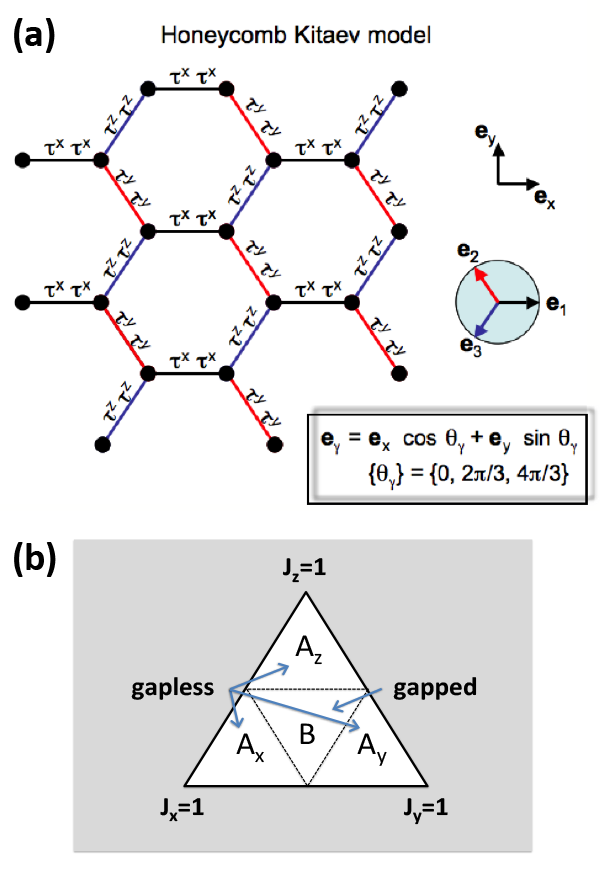
Kitaev’s model reveals the following picture. There are two fermion branches: the propagating and the localized ones. Localized fermions enter the Hamiltonian as a $Z_{2}$ gauge field, in turn creating a landscape for the propagating Majoranas. As a result, the Hamiltonian of the propagating Majoranas is a simple one: it describes noninteracting particles in a static gauge field. The ground state is uniform. Excitations of the gauge field are vortices, called visons, that carry magnetic flux and act as static defects that scatter propagating fermions. The model predicts two phases; in one of them the fermions are gapless and in the other they are gapped [see Fig. 1(b)].

Kitaev’s solution is, so far, just a mathematical beauty, but the work of Moessner and co-workers [5] suggests how to reveal it to the outside world: Their calculations show the presence of Majoranas could be established through a measurable quantity—the spin response to a time-dependent magnetic field (the dynamical spin susceptibility). Measurements should reveal a paradox. Namely, the specific-heat measurements will demonstrate the presence of gapless excitations, but these gapless excitations will not appear in the spin-spin correlation functions. And this is despite the fact that the fermions arise as collective excitations of the spin system. The spin-spin correlation functions remain short ranged because a spin flip involves both propagating and nonpropagating fermions. This should reveal itself in the dynamical correlation function.

The work by Moessner and co-workers provides a solid foundation for these general expectations in the form of rigorous calculations of the dynamical spin susceptibility [ $χ (ω, q)$ as a function of frequency $ω$ and wave vector $q$ ]. $χ (ω, q)$ is measurable, for instance, by neutron scattering and carries information about the excitation spectrum, showing how the system responds to the flip of a single spin. Such flip changes the total spin projection by one Planck constant, and if the excitation carries spin $1$ , the imaginary part of $χ$ has a sharp peak at the frequency corresponding to the dispersion of the excitation. The authors’ calculations—considerably more complicated than the Hamiltonian diagonalization used to solve Kitaev’s model—required numerical treatment and demonstrated that in the Kitaev model the imaginary part of $χ$ displays a spectral gap followed by an incoherent continuum. Thus, despite being gapless particles, the propagating Majoranas do not appear in the low-energy spin response—a very unusual situation.

The results may give us valuable insights on other quantum liquids, for example, QSL on a kagome lattice (an arrangement composed of interlaced triangles, whose name comes from a Japanese woven bamboo pattern) [6,7]. But the finding may have broader implications: Models of QSL belong to the general class of so-called lattice gauge theories where particles are coupled to each other by strong dynamical interactions. Such theories are considered not just in condensed matter but also in particle physics. The present solution may thus provide us with an alternative angle to view lattice gauge theories.

References

A. Yu. Kitaev, “Anyons in an Exactly Solvable Model and Beyond,” Ann. Phys. 321, 2 (2006)
J. Knolle, D. L. Kovrizhin, J. T. Chalker, and R. Moessner, “Dynamics of a Two-Dimensional Quantum Spin Liquid: Signatures of Emergent Majorana Fermions and Fluxes,” Phys. Rev. Lett. 112, 207203 (2014)
L. Balents, ”Spin Liquids in Frustrated Magnets,” Nature (London) 464, 199 (2010)
G. Jackeli and G. Khaliullin, “Mott Insulators in the Strong Spin-Orbit Coupling Limit: From Heisenberg to Quantum Compass and Kitaev Model,” Phys. Rev. Lett. 102, 017205 (2009)
A. P. Ramirez, “Strongly Geometrically Frustrated Magnets,” Annu. Rev. Mater. Sci. 24, 453 (1994)
T.-H. Han et al., “Fractionalized Excitations in the Spin-Liquid State of a Kagome Lattice Antiferromagnet,” Nature (London) 492, 406 (2012)
Y. Wan and O. Tchernyshyov, “Phenomenological $Z_{2}$ Lattice Gauge Theory of the Spin-Liquid State of the Kagome Heisenberg Antiferromagnet,” Phys. Rev. B 87, 104408 (2013)

About the Author

Alexei M. Tsvelik holds a Ph.D. in theoretical physics from the Kurchatov Institute for Atomic Energy. From 1982 to 1989 he worked at the Landau Institute for Theoretical Physics and then held various research positions in the US (Harvard, Princeton, and University of Florida). He was a lecturer and professor at the University of Oxford between 1992 and 2001. Since 2001, he has been a senior physicist at Brookhaven National Laboratory. He is an APS Fellow and a recipient of the Alexander von Humboldt prize (2014). He has authored two books with Cambridge University Press and 184 papers in refereed journals. In 2009 he was recognized as an Outstanding Referee by the American Physical Society.