Shaping the Future of Quantum Computation
Entanglement is “the characteristic trait of quantum mechanics,” as Schrödinger phrased it in the early days of quantum theory in 1935. It is, however, not only a fundamental physical phenomenon that exhibits counterintuitive correlations between two or more distant objects. Especially when shared by many different entities, entanglement is a resource for applications in quantum information, such as quantum communication networks or even quantum computation.
Proper entangled states for such applications require significant engineering and are typically not available at the push of a button. Only specific forms of entanglement are directly obtainable as the output of a laser light source, when the laser operates in the frequency-comb regime (with many equally spaced spectral components) and when its frequency modes are subject to the effect of parametric down-conversion (with a single photon converted into a photon pair whose total energy equals that of the input photon). However, in Physical Review A, R. Medeiros de Araújo, from the Kastler Brossel Laboratory, France, and colleagues report an optical experiment [1], in which they show that a much larger variety of multimode entangled states is already embedded in a down-converted frequency comb—including states of immediate use in quantum information processing. To reveal the different entangled states, their trick is to choose the right spectral-mode basis both for the source and the detector, with no need for changing the optical elements at different target states. In a way, this is like a painter who first mixes together all the different colors on the palette and then applies the new colors with a paintbrush in any desired form.
Quantum states containing entanglement between many parties, such as many qubits, may be represented in terms of mathematical graphs, where the connections between two nodes (corresponding to, e.g., two qubits) of the graph usually indicate the bipartite entangling interactions or gates used to build up the entire graph state. The most important graph of this type is an arbitrarily large two-dimensional lattice, representing a so-called cluster state—a state that can be used for quantum computation [2]. This particular form of quantum computation corresponds to a “one-way” quantum computer, where a quantum algorithm is run by sequentially performing irreversible, projective measurements on the individual nodes of a fixed cluster state. It is unlike the standard, “two-way” circuit model of quantum computation, where each quantum circuit consists of a sequence of unitary quantum gates that transform the input states in a nontrivial but reversible fashion. Universality is achieved in the one-way model by an appropriate choice of the measurement basis for each node, including a possible adjustment of the bases in later measurements, depending on the outcomes of earlier measurements.
On the more practical side, the one-way cluster-state model turned out to be very attractive for experimentalists: proof-of-principle demonstrations of elementary quantum computer components no longer depended on a robust implementation of certain quantum gates, but rather on the efficient generation of certain quantum states. Once created, gates can be obtained from these states by simply looking at parts of the states through measurements. For instance, a supply of two-qubit entangling gates is already contained in the connections of a multiqubit cluster state and these gates can be applied at any time upon signal qubits that propagate through the cluster. In a quantum optical implementation, the specific choice of encoding (i.e., how the state is represented in terms of optical properties) then determines which is harder: engineering a general-purpose quantum state or adjusting the measurement apparatus in a sufficiently general way.
A traditional way to encode a qubit optically is in the two orthogonal polarizations of a single photon. In this setup, measuring one qubit (i.e., photon) in an arbitrary (polarization) basis is easy, but entangling two or more qubits (i.e., photons) is hard. Such entangling operations are either probabilistic, or they require impractically strong nonlinear interactions in order to make the individual photons “talk to each other.” Moreover, even the production of single photons or some small-scale entangled states of a very few photons based on parametric down-conversion is rather inefficient, as it must be “heralded” by one or more photon detector clicks. Building large-scale multiphoton entanglement from these elementary sources is therefore a demanding task and its potential use for quantum computation depends on the scaling of all these probabilistic elements together with methods for storing and recycling incomplete cluster states.
Unlike the discrete polarization degree of freedom, the more natural encoding of an optical quantum state into the continuous amplitude and phase variables of a quantized optical mode enables one to create multimode entanglement from optical parametric sources on demand. This type of entanglement, the entanglement between many distinct optical modes instead of many photons, may also serve, in principle, as a resource for quantum computation [3], while realizing a sufficiently complete, “universal” set of measurements is the hardest part in this case.
Creating multimode entanglement relies on sources of nonclassical light with a Heisenberg uncertainty squeezed along one direction in phase space (that is, the uncertainty in one variable is allowed to be large, while the uncertainty in the conjugate variable is made small, with both together satisfying the Heisenberg relation). Producing highly squeezed light in a robust and efficient way is now state of the art. However, building a quantum state from it that is a suitable resource for processing quantum information has still required a certain amount of optical engineering—either including sufficient space on an optical table densely filled up with optical elements for coupling many spatial light modes [4,5] or including time delays for synchronization when coupling many temporal light modes [6–8]. And here is where the experiment of Medeiros de Araújo et al. [1] comes in.
The optical modes in their scheme are no longer described in space or time, but rather by a spectrum of frequencies. As a consequence, Medeiros de Araújo et al. [1] no longer rely on independent single-mode squeezed states, obtained either from arrays of independent parametric sources [4,5] or in the form of a train of independent pulses from a single parametric source [6–8]. For them it becomes unnecessary to build every graph state from scratch by putting all these different pieces together in space or time, always in a different arrangement depending on the desired state.
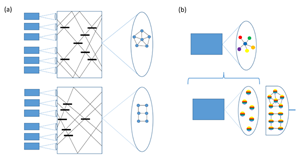
Instead, Medeiros de Araújo et al. [1] exploit the fact that large multimode squeezed states can be generated directly from a single optical parametric oscillator if it is pumped synchronously with laser light. In fact, the multimode squeezing that is present in the frequency comb of the output already gives a multimode entangled graph state (see Fig. 1). However, this state is represented by a very specific graph, not automatically corresponding to a proper resource for quantum computing. The compact, spectral approach for creating such graph states directly from an optical parametric oscillator is not completely new [7,9]. The news here is that by measuring in a basis of disentangled “supermodes,” with each supermode being a coherent mixture of all the original color-modes in the frequency comb, again a large set of independent single-mode squeezed states becomes available—as a kind of intrinsic, irreducible resource [10]. What Medeiros de Arajo et al. [1] effectively do is to project these independent squeezed states onto various six-mode graph states. In their experiment, this can be achieved by means of frequency-resolved homodyne detection with a pulse-shaped local oscillator. In other words, the shape of the local-oscillator pulse determines the shape of the resulting graph state, with no need for changing the optical setup at any stage.
After further experimental improvements, this scheme should become a versatile method for building “user-friendly” entangled states of up to 100 frequency modes. Besides full scalability, an open question with regards to this frequency-comb approach is whether for its use in “universal” quantum computation, the spectral modes can be also addressed individually and sequentially by measurements in order to be able to change the measurement bases during a computation. A big issue is fault tolerance, which is a challenge common to all intrinsically imperfect, continuous-variable one-way quantum computers based on finitely squeezed quantum optical states. Even ideally, without any external losses and errors, quantum error correction will be necessary from the start [11].
References
- R. Medeiros de Araújo, J. Roslund, Y. Cai, G. Ferrini, C. Fabre, and N. Treps, “Full characterization of a highly multimode entangled state embedded in an optical frequency comb using pulse shaping,” Phys. Rev. A 89, 053828 (2014)
- R. Raussendorf and H. J. Briegel, “A One-Way Quantum Computer,” Phys. Rev. Lett. 86, 5188 (2001)
- N. C. Menicucci, P. van Loock, M. Gu, C. Weedbrook, T. C. Ralph, and M. A. Nielsen, “Universal Quantum Computation with Continuous-Variable Cluster States,” Phys. Rev. Lett. 97, 110501 (2006)
- P. van Loock, C. Weedbrook, and M. Gu, “Building Gaussian Cluster States by Linear Optics,” Phys. Rev. A 76, 032321 (2007)
- M. Yukawa, R. Ukai, P. van Loock, and A. Furusawa, “Experimental Generation of Four-Mode Continuous-Variable Cluster States,” Phys. Rev. A 78, 012301 (2008)
- N. C. Menicucci, X. Ma, and T. C. Ralph, “Arbitrarily Large Continuous-Variable Cluster States from a Single Quantum Nondemolition Gate,” Phys. Rev. Lett. 104, 250503 (2010)
- N. C. Menicucci, S. T. Flammia, and O. Pfister, “One-Way Quantum Computing in the Optical Frequency Comb,” Phys. Rev. Lett. 101, 130501 (2011)
- S. Yokohama et al., “Ultra-Large-Scale Continuous-Variable Cluster States Multiplexed in the Time Domain,” Nature Photon. 7, 982 (2013)
- M. Chen et al., “Experimental Realization of Multipartite Entanglement of 60 Modes of a Quantum Optical Frequency Comb,” Phys. Rev. Lett. 112, 120505 (2014)
- S. L. Braunstein, “Squeezing as an Irreducible Resource,” Phys. Rev. A 71, 055801 (2005)
- N. C. Menicucci, “Fault-Tolerant Measurement-Based Quantum Computing with Continuous-Variable Cluster States,” Phys. Rev. Lett. 112, 120504 (2014)