A Critical Test of Quantum Criticality

Martin Klanjšek

Viewpoint

A Critical Test of Quantum Criticality

Jožef Stefan Institute, Jamova cesta 39, 1000 Ljubljana, Slovenia

July 14, 2014• Physics 7, 74

Theoretically predicted quantum critical behavior in a model magnetic material has been experimentally confirmed at a quantitative level.

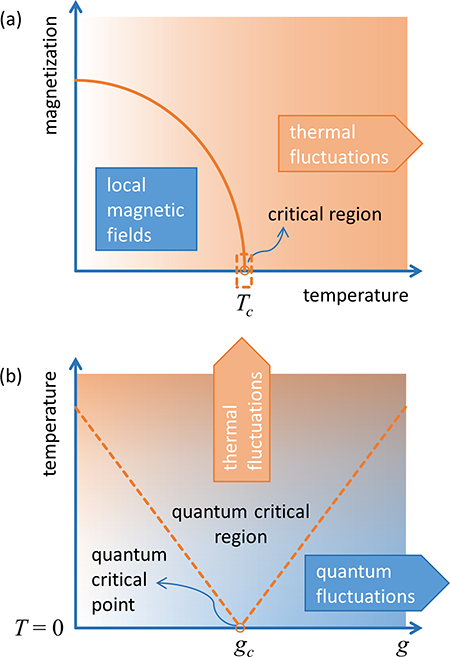
Figure caption — **Figure 1:** (a) An example of the classical phase transition in a ferromagnet. Thermal fluctuations causing the random reorientation of the constituent spins grow with temperature. They compete with the tendency of the local magnetic fields to align the spins. As a result, the net magnetization in the ordered state continuously decreases with temperature (orange line) and drops to zero at a critical temperature $T_{c}$ , surrounded by a narrow critical region (dashed rectangle). (b) A generic example of the quantum phase transition. Quantum fluctuations controlled by the nonthermal parameter $g$ lead to a similar phase transition at a critical value $g_{c}$ , the so called quantum critical point, already at zero temperature, $T = 0$ . Their interplay with thermal fluctuations opens up a progressively broader, V-shaped quantum critical region extending much above the zero temperature (dashed lines).

Every physicist knows how a ferromagnet like iron behaves as the temperature is increased [Fig. 1(a)]. At low temperatures, the constituent spins are spontaneously aligned as a result of the local magnetic fields from neighboring spins. Thermal fluctuations act against such local fields, inducing random reorientation of the spins. As the temperature increases, thermal fluctuations grow and the net magnetization in the ordered state continuously decreases. The magnetization drops to zero at a critical temperature $T_{c}$ ( $1043$ kelvin in the case of iron). In a narrow temperature range around $T_{c}$ , thermal fluctuations of the spins extend over all length scales of the material—scale invariance is a key feature of critical points. This is an example of a continuous classical phase transition driven by thermal fluctuations.

Fluctuations driving quantum phase transitions are of a different nature, however. For example, a continuous quantum phase transition [1–3] is driven by quantum fluctuations resulting from Heisenberg’s uncertainty principle. The transition takes place when the material is at zero temperature but as a function of a nonthermal control parameter, such as applied pressure, an external magnetic field, or the density of electrons manipulated by the chemical composition. Theory has predicted that, surprisingly, an additional presence of thermal fluctuations at finite temperatures does not eliminate the critical fluctuations present around the quantum critical point [4]. Instead, the region of quantum criticality becomes progressively broader with increasing temperature and extends to temperatures significantly above zero [Fig. 1(b)]. This has now been experimentally demonstrated by Alison Kinross and her colleagues at McMaster University, Canada, in cooperation with theorist Subir Sachdev from Harvard University. In a paper in Physical Review X [5], they report the phase diagram of ${CoNb}_{2} O_{6}$ , a model magnetic material for quantum criticality [6]. Their results correspond perfectly to the general phase diagram outlined in Fig. 1(b). Furthermore, they provide the first quantitative confirmation of any theory—although there are not many—aiming to predict the temperature evolution of the quantum critical behavior. Although the work by Kinross et al. is concerned with a particular compound, the results are important in a broader sense. Namely, the quantum critical behavior observed in such diverse systems as metals, magnets, superconductors, gases of cold atoms, and black holes, shares many fundamental characteristics—universality is another key feature of critical points.

Research on quantum criticality in the past two decades has focused on heavy-fermion metals [2,3]. These are characterized by large effective masses of the conduction electrons as a consequence of narrow electronic bands. The correspondingly small energy scale can be easily overcome, which makes heavy-fermion metals susceptible to external perturbations: some of them can be brought to the quantum critical point separating a metallic from an antiferromagnetic state by changing chemical composition, magnetic field, or external pressure. The intricate competition between the two phases results in unusual and interesting properties that are still poorly understood. Since many degrees of freedom are involved, i.e., charge, orbital, and spin, the theories describing these systems are quite complex and, to date, unsatisfactory. This is even more the case for materials such as the two classes of high-temperature superconductors: cuprates and iron-based superconductors. Adding to the complexity, the quantum critical point is surrounded by the superconducting phase and other unusual phases at higher temperatures, rendering the theoretical treatment even harder.

To better understand the experiments focused on quantum criticality, a smaller number of relevant degrees of freedom should be involved, which brings us to magnetic insulators. These materials contain spins of magnetic ions, coupled via the exchange interaction, as the only degree of freedom. They are particularly appealing when two conditions are met. First, exchange couplings should be sufficiently small with respect to the energy scales set by temperature or magnetic fields that can be reached. This condition allows the experimental investigation of the entire phase diagrams of Fig. 1(b), with magnetic field as the control parameter. Second, when the exchange-coupling network contains one-dimensional motifs like chains (lines of spins) or ladders (pairs of parallel chains), the theoretical approaches developed specifically for the simplest case of one dimension allow deeper understanding and even, in some cases, lead to analytical results [1,7].

A nice example is ${CoNb}_{2} O_{6}$ [6] where spins are ferromagnetically coupled into Ising chains. This means that each spin can point only up or down, along an “easy” axis determined by the crystal structure. Because of its simplicity, the underlying spin model is one of a few where rigorous predictions exist for nonzero temperatures and magnetic fields, including the quantum critical region [1]. In the ground state, all spins point in the same direction, either up or down, creating a ferromagnet. A relatively small exchange coupling (corresponding to a temperature of around $18$ kelvin) allows this state to be manipulated by a magnetic field. When the field is applied in the direction perpendicular to the easy axis and gradually increased to $5.2$ tesla, the system enters the paramagnetic ground state with spins oriented along the field, i.e., perpendicular to their initial configuration. The fundamental difference between the two states is that the ferromagnetic one breaks the mirror symmetry of the Ising chain, while the paramagnetic one does not. Hence the two states are clearly separated by a phase transition and, as the ground states are associated with zero temperature, this transition is a quantum critical point. Theory says that the nature of quantum fluctuations in both states is different: the motion of domain walls separating two oppositely oriented, ferromagnetic domains in the first case, and single-spin flips in the second.

The researchers at McMaster University have now studied the nature of the quantum fluctuations across the entire phase diagram of ${CoNb}_{2} O_{6}$ . They used nuclear spin-lattice relaxation, one of the basic tools of nuclear magnetic resonance, as an observable related to low-energy spin fluctuations [8,9]. In a typical experiment of this sort, an external radio-frequency pulse is used to disrupt the selected set of nuclear spins, whose relaxation due to the coupling with magnetic spin fluctuations (constituting the lattice) is then monitored. Existing rigorous theoretical predictions combined with a few phenomenological simplifications allowed the researchers to obtain analytic expressions for the behavior of their observable in all three regions: the two magnetic phases and the region of quantum criticality separating them. The spin fluctuations are expected to exhibit the energy gap whose evolution with the magnetic field is basically represented by dashed lines in Fig. 1(b). The energy gap, which represents the only intrinsic energy scale of the problem, drops to zero at the critical field. The only remaining energy scale is then set by temperature, this being the crucial property of quantum criticality [1–3]. The researchers experimentally confirmed the predicted linear evolution of the gap with the magnetic field, which allowed them to pinpoint the location of the quantum critical point. At the critical field, the observable is expected to display a power-law temperature dependence, another hallmark of quantum criticality, with a characteristic power of - $3 / 4$ in this case—precisely what they observed. Even more, a rigorous experimental analysis allowed them to estimate the prefactor to this behavior, which they found to correspond nicely to the theoretically predicted one. And finally, they observed this behavior to persist to as high a temperature as almost half of the exchange coupling, which sets the global energy scale of the problem. This answers an essential question about how far away from the absolute zero temperature quantum criticality reaches or how measurable it really is. The experiment constitutes the first quantitative confirmation of the quantum critical behavior predicted by any of the few existing theories.

This work complements a series of previous nuclear-magnetic-resonance studies of quantum criticality in other magnetic insulators containing spin chains or ladders. For instance, the pioneering experimental work of Chaboussant et al. [10] mapped the phase diagram of Fig. 1(b) in a ladder compound. Yet in that case, the complexity of the system and the lack of relevant theoretical predictions prevented the authors from learning much about quantum criticality. More recent work [11] demonstrated scale invariance and universality of the quantum critical behavior by comparing data for two model materials. These two results and some others established nuclear magnetic resonance as a method of choice, and magnetic insulators as the materials of choice, for studying quantum criticality. Obvious future directions involve materials containing spins arranged in two-dimensional motifs. In this respect, it is worth noting a recent approach that relates quantum critical theories with theories of gravity in black holes, which has already led to the first experimental predictions on the dynamics of quantum criticality [12].

Quantum critical behavior found in diverse systems ranging from simple magnets to sophisticated black holes may well reflect one of the most complex states of matter. But approaches like that of Kinross et al. are a step forward in our effort to arrive at the general theory of this universal behavior, the project already realized for classical criticality after decades of work [13].

References

S. Sachdev, Quantum Phase Transitions (Cambridge University Press, Cambridge, 1999)[Amazon][WorldCat]
S. Sachdev and B. Keimer, “Quantum Criticality,” Phys. Today 64, No. 2, 29 (2011)
P. Coleman and A. J. Schofield, “Quantum Criticality,” Nature 433, 226 (2005)
A. Kopp and S. Chakravarty, “Criticality in Correlated Quantum Matter,” Nature Phys. 1, 53 (2005)
A. W. Kinross, M. Fu, T. J. Munsie, H. A. Dabkowska, G. M. Luke, Subir Sachdev, and T. Imai, “Evolution of Quantum Fluctuations Near the Quantum Critical Point of the Transverse Field Ising Chain System ${CoNb}_{2} O_{6}$ ,” Phys. Rev. X 4, 031008 (2014)
R. Coldea, D. A. Tennant, E. M. Wheeler, E. Wawrzynska, D. Prabhakaran, M. Telling, K. Habicht, P. Smeibidl, and K. Kiefer, “Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E $_{8}$ Symmetry,” Science 327, 177 (2010)
T. Giamarchi, Quantum Physics in One Dimension (Oxford University Press, Oxford, 2004)[Amazon][WorldCat]
T. Moriya, “Nuclear Magnetic Relaxation in Antiferromagnetics,” Prog. Theor. Phys. 16, 23 (1956)
M. Horvatić, C. Berthier, “NMR Studies of Low-Dimensional Quantum Antiferromagnets,” in High Magnetic Fields: Applications in Condensed Matter Physics and Spectroscopy, edited by C. Berthier, L. P. Levy, and G. Martinez, Lecture Notes in Physics (Springer-Verlag, Berlin, 2002), p. 200[Amazon][WorldCat]
G. Chaboussant, Y. Fagot-Revurat, M.-H. Julien, M. E. Hanson, C. Berthier, M. Horvatić, L. P. Lévy, and O. Piovesana, “Nuclear Magnetic Resonance Study of the $S = 1 / 2$ Heisenberg Ladder Cu $_{2}$ (C $_{5}$ H $_{12}$ N $_{2}$ ) $_{2}$ Cl $_{4}$ : Quantum Phase Transition and Critical Dynamics,” Phys. Rev. Lett. 80, 2713 (1998)
S. Mukhopadhyay, M. Klanjšek, M. S. Grbić, R. Blinder, H. Mayaffre, C. Berthier, M. Horvatić, M. A. Continentino, A. Paduan-Filho, B. Chiari, and O. Piovesana, “Quantum-Critical Spin Dynamics in Quasi-One-Dimensional Antiferromagnets,” Phys. Rev. Lett. 109, 177206 (2012)
W. Witczak-Krempa, E. S. Sørensen, and S. Sachdev, “The dynamics of Quantum Criticality Revealed by Quantum Monte Carlo and Holography,” Nature Phys. 10, 361 (2014)
C. Domb, The Critical Point: a Historical Introduction to the Modern Theory of Critical Phenomena (Taylor & Francis, London, 1996)[Amazon][WorldCat]

About the Author

Martin Klanjšek is a Research Associate at Jožef Stefan Institute in Ljubljana, Slovenia. After obtaining his Ph.D. at the University of Ljubljana in 2004, he worked as a postdoctoral researcher from 2007 to 2008 and as an occasional visiting researcher from 2009 to 2012 in the laboratory for high magnetic fields, LNCMI, in Grenoble, France. His research focuses on strongly correlated electron systems, superconductivity, complex metallic alloys and quasicrystals, with nuclear magnetic resonance as his main experimental tool.