Solitons with a Twist
In the past few years, ultracold atoms have emerged as a novel playground in which to study collective behavior that occurs in superconductors, neutron stars, and other media. The advantage of using ultracold atoms is that their properties can be controlled at will, providing a tunable platform to study various macroscopic phenomena, including phase transitions. A characteristic feature of certain types of phase transitions is the formation of inhomogeneities, or topological defects, which can offer a window into the dynamics of the transition. These defects, which appear as walls, lines, and rings, can last for a long time after the phase transition is complete. However, recent experiments by two independent groups found that certain defects, initially identified as wall-like “solitons,” lasted longer than expected in ultracold atoms confined in an elongated trap. Now, reporting in Physical Review Letters, these same groups have performed follow-up experiments that reveal the defects’ identity had been mistaken. The observed defects are actually “solitonic vortices,” which are vortices constrained in all but one dimension [1,2]. The findings eliminate the discrepancy between experiment and theory, and it demonstrates that a rich variety of defects may be explored in ultracold atoms.
In a simple picture, some phase transitions can be seen as the passage from a disordered to an ordered phase of matter. One of the most popular and well-studied phase transitions is the para/ferromagnetic transition in magnetic compounds such as iron. In this transition the order parameter (a measure of the degree of order in the system) is the spontaneous magnetization of the sample. In the disordered (paramagnetic) phase, the individual atomic spins point in random directions, leading to zero global magnetization, while in the ordered ferromagnetic phase they all point in the same direction and sum up to create a finite macroscopic magnetization. Physicists wanting to understand this transition can’t go in and fine-tune the spin interactions that drive it. But the same physics can be mimicked by certain types of ultracold-atom systems: conventional (spinless) superfluids resemble magnetic media and certain experimental parameters can be used as knobs that allow some control over atomic interactions.
In the case of a superfluid, the order parameter is the macroscopic wave function of the system. This is a complex number, which can be represented in the complex plane as a two-dimensional arrow, reminiscent of the magnetization of a magnetic system, with the phase of the complex number playing the role of the orientation of the magnetization. At sufficiently cold temperature, the superfluid goes through a phase transition (Bose-Einstein condensation), in which the wave functions’ complex phases line up in an ordered (coherent) arrangement.
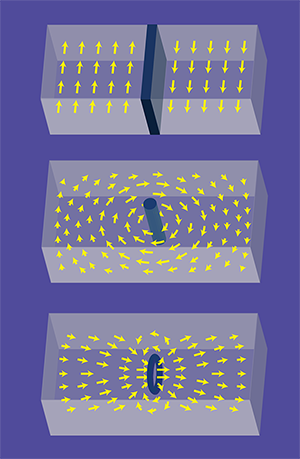
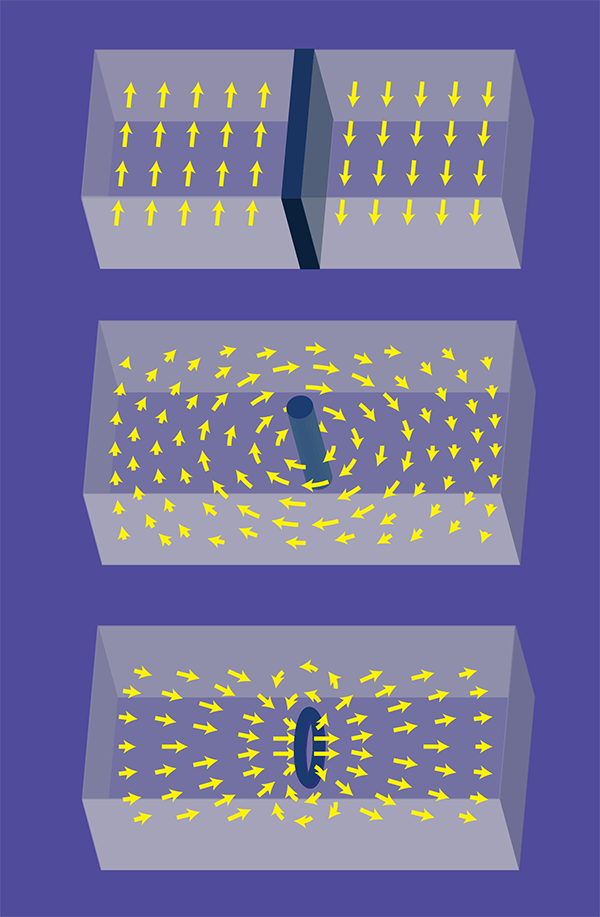
The ordered phase is usually homogeneous inside a material, but spatiotemporal fluctuations and defects of the order parameter exist and can play an important role in the dynamics and thermodynamic properties of the material. Defects can be classified based on their different topologies. The simplest defects are solitons, which are solitary waves or discontinuous steps that maintain their shape during propagation. In a magnetic compound these solitons would correspond to domain walls separating regions of different magnetization and where the direction of magnetization is abruptly reversed. In a superfluid, a soliton would be a π shift (half turn) in the phase of the wave function. In the absence of long-range interactions, these defects are unstable against bending or “snaking” in the plane that separates the different regions. The only way to stabilize a soliton in a system defined by short-range interactions is to confine it transversally to kill these unstable snaking modes. Other types of defects are vortices and vortex rings, in which the order parameter winds around either an open line or a closed loop, respectively (see Fig.1).
These topological defects play an important role in the theory of critical phenomena, such as magnetic and superconducting transitions. Defects often correspond to strongly excited states in these systems, but their topological nature confers them a very long lifetime. A famous example is the Kibble-Zurek mechanism [3], which concerns second-order transitions. The relaxation time for these transitions diverges at the critical temperature Tc, so one can argue that there’s not enough time for the system to reach its lowest energy state if the cooling rate is relatively fast. The Kibble-Zurek model thus predicts that topological defects will form and live for a very long time, even after leaving the critical region around Tc. The Kibble-Zurek mechanism was first proposed in cosmology, as phase transitions in the early Universe may have produced long-lasting defects in the form of cosmic strings, but it was later confirmed in superfluid helium.
To understand the physics of these topological defects, in 2013 two experimental groups attempted to study solitons in different ultracold-atom systems. The first group led by Martin Zwierlein from the Massachusetts Institute of Technology (MIT), Cambridge, looked at fermionic atoms, specifically lithium- 6 [4], while Gabriele Ferrari at the University of Trento in Italy and his team investigated bosonic sodium atoms [5]. In both these experiments, clouds of atoms were trapped and cooled down to temperatures of the order of 100 nanokelvin, where superfluidity occurs. The optical traps confined the atoms into an elongated shape to hopefully prevent the snaking instability that disrupts solitons. To observe the topological defects in a particular cloud, both teams cast the cloud’s shadow on a CCD camera using resonant light. Defects appeared as slits or holes in these projections because the superfluid wave function (or density) goes to zero in regions where the order parameter abruptly reverses.
The two experiments differed in the way the solitons were generated. In the MIT experiment, the researchers tried to nucleate a soliton in a controlled way using a phase imprinting method that was successfully used in the past to generate solitons in Bose-Einstein condensates [6,7]. Zwierlein and his colleagues observed a reduced-density slit running through the middle of their cloud, which they interpreted as a soliton. This presumed soliton oscillated from one end of the trap to the other, as expected from quantum many-body calculations. However, the rate of oscillation was 8 times slower than predicted [4]. A similar discrepancy was detected at around the same time by the Trento group. Ferrari and his colleagues generated defects through the Kibble-Zurek mechanism (i.e., with a rapid temperature quench) in an elongated cloud of ultracold bosonic atoms, but they found the lifetimes of the solitonlike defects that they observed were surprisingly long compared to predictions [5].
As mentioned above, solitons exist only in purely one-dimensional systems. In three dimensions they are unstable and decay through snaking instability. It was suggested that the two groups were not really observing solitons but rather the decay product of their instability. If, for example, the defects were vortex rings [8], then the images on a CCD camera would show low-density line segments that could be mistaken for the full lines that characterize solitons.
The two groups decided to carry out further experimental studies to clarify the nature of the defects they observed experimentally. The MIT group performed a three-dimensional tomographic reconstruction of the defect and beautifully showed that it was neither planar nor circular as would be expected for a soliton or a vortex ring. Instead, the defect was a single straight vortex line [1], which in the constrained geometry of the cloud is called a solitonic vortex. The anomalously small oscillation frequency of the defect could then be interpreted as the well-known precession frequency of a vortex in a confined geometry. The Trento group, for their part, used matter interferometry to detect a twist in the low-density defect region, which they showed is indicative of a solitonic vortex [2]. They argued that the solitonic vortex is a long-lasting remnant of a soliton that decays by the snaking instability.
This story illustrates the universality of the physics of critical phenomena. Two groups tried to observe the same objects (solitons) in different systems. They met the same kind of anomalous results, for which, in the end, a common explanation was found. Now that the nature of these defects has been identified, one needs to clarify experimentally their physical properties. Solitonic vortices were proposed to bridge the gap between solitons and vortices, so they have elements of both. Like vortices, their phase swirls around the defect, but only in a small region of space. Outside this region, the phase becomes homogeneous, like the phase on either side of a soliton. Since the phase difference of the wave function on the two sides of the solitonic vortex can, in principle, be determined by measuring the vortex’s velocity, future experimental efforts should be able to confirm the solitonic nature of the solitonic vortex.
References
- Mark J. H. Ku, Wenjie Ji, Biswaroop Mukherjee, Elmer Guardado-Sanchez, Lawrence W. Cheuk, Tarik Yefsah, and Martin W. Zwierlein, “Motion of a Solitonic Vortex in the BEC-BCS Crossover,” Phys. Rev. Lett. 113, 065301 (2014)
- Simone Donadello, Simone Serafini, Marek Tylutki, Lev P. Pitaevskii, Franco Dalfovo, Giacomo Lamporesi, and Gabriele Ferrari, “Observation of Solitonic Vortices in Bose-Einstein Condensates,” Phys. Rev. Lett. 113, 065302 (2014)
- T. W. B. Kibble, “Topology of Cosmic Domains and Strings,” J. Phys. A 9, 1387 (1976); W. H. Zurek, “Cosmological Experiments in Superfluid Liquid Helium?” Nature 317, 505 (1985)
- T. Yefsah, A. T. Sommer, M. J. H. Ku, L. W. Cheuk, W. Ji, W. S. Bakr, and M. W. Zwierlein, “Heavy Solitons in a Fermionic Superuid,” Nature 499, 426 (2013)
- G. Lamporesi, S. Donadello, S. Serafini, F. Dalfovo, and G. Ferrari, “Spontaneous Creation of Kibble-Zurek Solitons in a Bose-Einstein Condensate,” Nature Phys. 9, 656 (2013)
- S. Burger, K. Bongs, S. Dettmer, W. Ertmer, and K. Sengstock, “Dark Solitons in Bose-Einstein Condensates,” Phys. Rev. Lett. 83, 5198 (1999)
- J. Denschlag et al., “Generating Solitons by Phase Engineering of a Bose-Einstein Condensate,” Science 287, 97 (2000)
- A. Bulgac, M. McNeil-Forbes, M. M. Kelley, K. J. Roche, and G. Wlazlowski, “Quantized Superuid Vortex Rings in the Unitary Fermi Gas,” Phys. Rev. Lett. 112, 025301 (2014)