Testing a Realistic Quark-Gluon Plasma

Gert Aarts

Viewpoint

Testing a Realistic Quark-Gluon Plasma

Department of Physics, College of Science, Swansea University, United Kingdom

August 18, 2014• Physics 7, 86

More realistic versions of lattice QCD may lead to a better understanding of how quarks formed hadrons in the early Universe.

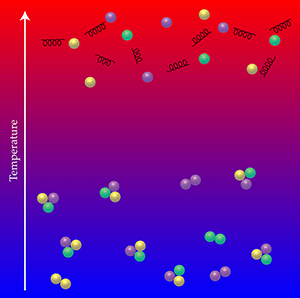
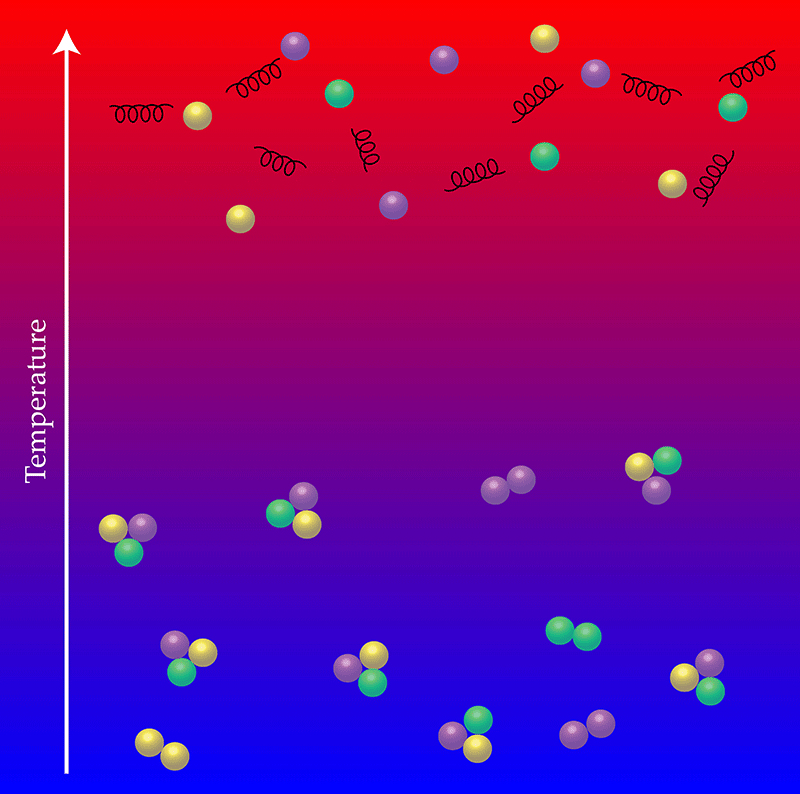
Figure caption — **Figure 1:** At everyday temperatures, quarks are confined in hadrons (such as protons, neutrons and pions). But at the energy densities accessible at particle accelerators, quarks can become deconfined, forming a quark-gluon plasma—a phase reminiscent of the primordial Universe. Numerical simulations based on lattice quantum chromodynamics are helping physicists understand how the transition from the confined to the deconfined state occurs.

Under normal conditions, quarks and gluons are confined in the protons and neutrons that make up everyday matter. But at high energy densities—the range accessible at today’s particle accelerators—quarks and gluons form a plasma reminiscent of the primordial Universe after the big bang. Understanding how the transition (Fig. 1) from the confined state to this quark-gluon plasma (and vice versa) occurs is a fundamental goal of experiments at the Relativistic Heavy Ion Collider and the Large Hadron Collider, which recreate the plasma by colliding nuclei at ultrarelativistic speeds. Theorists are therefore looking for new ways to study the transition with quantum chromodynamics (QCD), the mathematically challenging theory that describes the strong interaction between quarks. In Physical Review Letters, researchers in the HotQCD Collaboration report an analysis of this phase transition using a formulation of QCD that lends itself to numerical solutions on a computer, called lattice QCD [1]. Their simulations of deconfinement—the first to be performed with a version of lattice QCD that accurately describes the masses and, in particular, the symmetries of the quarks—yield the critical temperature for the transition to occur, and show that it is a smooth crossover, rather than an abrupt change.

Quark interactions become weaker at high energies—a property called asymptotic freedom that is built into QCD. Based on this notion, theorists predicted the existence of the quark-gluon plasma in the 1970s [2]; but a quantitative study of how this transition occurs remains difficult to this day, both theoretically and experimentally. For instance, whether the transition is a smooth crossover or a proper phase transition depends on the mass values of the light quarks (the up, down, and strange quarks). The distinction is important: if quark confinement in the early Universe occurred as a phase transition, it might have left a detectable imprint, while a crossover would likely not have. Even in the case of a crossover, a change in the equation of state describing the quark matter might have affected the spectrum of gravitational waves resulting from the big bang, or the dark matter density.

To fully understand the details of the transition from the confined phase to the plasma phase, theorists need to study the problem from first principles. One such approach is based on lattice QCD, which is a version of QCD obtained by putting the quarks and gluons on a four-dimensional spacetime lattice. It is especially useful for numerical simulations, since it turns the problem of summing over all possible quantum configurations of quarks and gluons into a (very!) high-dimensional integral that can be estimated using statistical sampling. In a simulation, many configurations of quarks and gluons are generated numerically at different temperatures. The temperature of the plasma is determined via the lattice spacing $a$ and the extent of the lattice in the temporal direction, $N_{τ}$ , via the relation $T = 1 / (a N_{τ})$ . Simulations with lattice QCD have shown that the deconfinement transition is a crossover [3] with a characteristic transition temperature of $155$ mega-electron-volts ( $MeV$ ), or $2 \times 10^{12}$ $K$ [4,5]. Lattice QCD can also be used to compute the equation of state of the quark-gluon plasma, which is needed to describe the liquidlike behavior of the plasma measured at RHIC and the LHC.

One known problem with lattice QCD, however, is that it doesn’t accurately account for chiral symmetry in the hadronic phase—meaning the way that left-handed and right-handed quarks behave. (The handedness of a quark is defined by the direction of its spin relative to its momentum.) As observed experimentally and predicted by QCD, chiral symmetry is spontaneously broken when quarks form hadrons, and restored at high temperature; it is also explicitly broken by the finite mass of the quarks. But it turns out that, for mathematical reasons, chiral symmetry and the lattice discretization do not go well together [6]. To handle this incompatibility, a number of versions of lattice QCD exist, all of which have advantages and disadvantages.

The most widely applied version for studying QCD thermodynamics is the so-called “staggered fermion” formulation, in which different components of the quark field are distributed over the even and odd lattice sites. The formulation has several advantages: an exact chiral symmetry exists at finite lattice spacing, which is theoretically sound, and simulations are fairly inexpensive in terms of computational time. Hence all lattice results referred to above have in fact used staggered fermions. The downside, however, is that the staggered fermion formulation doesn’t properly describe the flavor symmetry of the quarks, except in the continuum limit, when the lattice spacing, $a$ , approaches zero.

The work from the HotQCD Collaboration is an attempt to validate the conclusions obtained with the staggered fermion approach. They use the so-called “domain wall fermion” formulation that carries the correct chiral and flavor symmetry, even at finite lattice spacing. But correctness comes at a cost, as the theory is formulated not in four but five dimensions: the four-dimensional chiral fermions live on domain walls in the fifth direction and chiral symmetry is exact at finite lattice spacing, provided that the domain walls are well separated. The extra dimension turns the numerical problem into a demanding high-performance computing challenge that requires an order of magnitude more computational time. To perform their calculations, the researchers therefore made use of the Blue Gene/Q supercomputer at Lawrence Livermore National Laboratory—the third fastest supercomputer in the world.

The authors report two main findings: the crossover temperature from the confined to the deconfined state occurs at $155 MeV$ , entirely consistent with the results from the staggered fermion approach, extrapolated to the continuum; and chiral symmetry is restored slightly above the crossover temperature, which was expected but had not been demonstrated before. However, a possible restoration of the $U (1)_{A}$ symmetry, yet another important symmetry associated with quarks that relates to the axial anomaly—a cornerstone in the development of the standard model of particle physics—happens at a much higher temperature, close to the highest temperature studied in the HotQCD Collaboration work, $195 MeV$ . This result requires further study: If it holds, this result will impact future model studies of the QCD phase transition, since they will have to accurately reproduce it as well.

One limitation of the authors’ analysis is that it is carried out on lattices with a fixed extent in the temporal direction, namely $N_{τ} = 8$ . Since the temperature of any one simulation is determined from the relation $T = 1 / (a N_{τ})$ , having a fixed extent in time sets a lower limit on the lattice spacing. From previous studies with the staggered fermion version of lattice QCD, it is known that the results obtained using coarse lattices can be misleading. Instead, a careful extrapolation to the continuum limit is required, which implies carrying out simulations at smaller values of $a$ and, therefore, larger values of $N_{τ}$ . The possibility exists that the excellent agreement with the continuum-extrapolated staggered result for the transition temperature ( $T_{c} \sim 155 MeV$ ) may be accidental. Simulations at a larger temporal extent would be needed to settle this, but this requires substantially larger computing resources, which may only become available in the future.

References

Tanmoy Bhattacharya et al. (HotQCD Collaboration), “QCD Phase Transition with Chiral Quarks and Physical Quark Masses,” Phys. Rev. Lett. 113, 082001 (2014)
N. Cabibbo and G. Parisi, “Exponential Hadronic Spectrum and Quark Liberation,” Phys. Lett. B 59, 67 (1975)
Y. Aoki, G. Endrodi, Z. Fodor, S. D. Katz, and K. K. Szabo, “The Order of the Quantum Chromodynamics Transition Predicted by the Standard Model of Particle Physics,” Nature 443, 675 (2006)
S. Borsanyi, Z. Fodor, C. Hoelbling, S. D. Katz, S. Krieg, C. Ratti, and K. K. Szabó “Is There Still Any $T_{c}$ Mystery in Lattice QCD? Results with Physical Masses in the Continuum Limit III,” J. High Energy Phys. 2010, 073 (2010)
A. Bazavov et al. (HotQCD Collaboration), “The Chiral and Deconfinement Aspects of the QCD Transition,” Phys. Rev. D 85, 054503 (2012)
H. B. Nielsen and M. Ninomiya, “Absence of Neutrinos on a Lattice. 1. Proof by Homotopy Theory,” Nucl. Phys. B 185, 20 (1981); Erratum, ibid. 185, 541 (1982)

About the Author

Gert Aarts is a professor of Physics in the Particle Theory group of the Physics Department in the College of Science at Swansea University in Wales, United Kingdom. After obtaining his Ph.D. at Utrecht University in the Netherlands, he did postdocs at the University of Heidelberg in Germany and the Ohio State University, before moving to Swansea in 2004. He works on QCD under extreme conditions and is currently the holder of a Royal Society Wolfson Research Merit Award and a Leverhulme Research Fellowship.

QCD Phase Transition with Chiral Quarks and Physical Quark Masses

Tanmoy Bhattacharya, Michael I. Buchoff, Norman H. Christ, H.-T. Ding, Rajan Gupta, Chulwoo Jung, F. Karsch, Zhongjie Lin, R. D. Mawhinney, Greg McGlynn, Swagato Mukherjee, David Murphy, P. Petreczky, Dwight Renfrew, Chris Schroeder, R. A. Soltz, P. M. Vranas, and Hantao Yin (HotQCD Collaboration)

Phys. Rev. Lett. 113, 082001 (2014)

Published August 18, 2014

Read PDF