Crossing a Quantum Fluid Divide
Understanding superfluidity and superconductivity in two dimensions (2D) has long challenged and intrigued physicists. In the early 1990s, 2D quantum fluids provided a preliminary model for the motion of electrons in layered high-temperature superconductors. Since then, alternative theories have been put forth, but there is growing interest in understanding how confinement to two dimensions can influence the flow of quantum particles. An exciting arena for studying 2D quantum fluids is atomic physics, where ultracold atoms have the advantage that their interactions can be fairly easily manipulated with electromagnetic fields. Writing in Physical Review Letters, Vasiliy Makhalov and colleagues from the Russian Academy of Sciences in Nizhniy Novgorod report measurements of the ground-state pressure of a 2D cloud of atoms as the binding between the atoms is increased. By monitoring the gas pressure, they were able to observe how pairs of these fermionic atoms transform into tightly bound bosonic molecules [1]. The properties of this fermion-to-boson crossover will help refine theories of strongly correlated quantum fluids in 2D.
One of the main motivations for studying quantum fluids is that they behave in many ways like superconductors. Below a certain transition temperature Tc the electrons in a superconductor conduct electricity without resistance, just as certain fluids can flow without viscosity below a transition temperature. Generally speaking, superconductivity occurs when electrons in a metal feel an attractive interaction and bind into pairs, as described by the Bardeen-Cooper-Schrieffer (BCS) theory of superconductivity. A similar pairing occurs in superfluids composed of interacting fermionic atoms. While the superconducting transition temperature is quite low in typical metals, much stronger binding and larger values of Tc are reached in special materials such as cuprates and pnictides. The physics underlying these high-temperature superconductors has not been fully resolved, but atomic physics may provide some insight into this solid-state physics problem. Recent advances have made it possible to realize very strong and tunable binding of trapped fermionic atoms, leading to high- Tc superfluids that may share important properties with high- Tc superconductors.
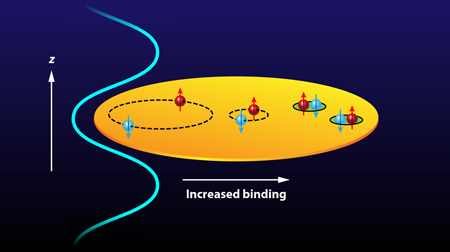
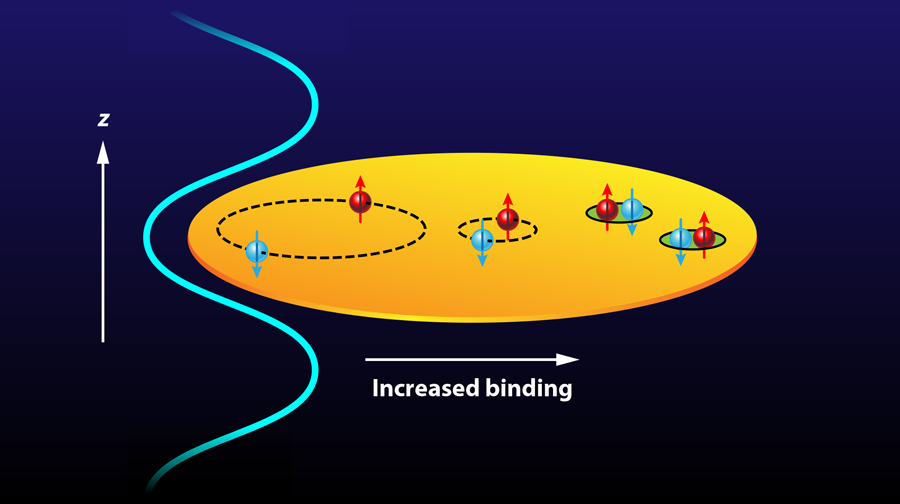
Below the transition temperature, the binding between atoms can affect their statistical distribution, which can be monitored by measuring the pressure of the gas. By the Pauli principle, fermions cannot occupy the same quantum state, and as such they try to keep a certain distance from each other. A gas of fermionic atoms therefore exhibits a finite ground-state pressure already by statistics, even without interaction. Once a weak attraction between the atoms is introduced, however, it becomes favorable for two distinct fermions (for instance, atoms in different spin states) to form a bound state, a so-called Cooper pair. An increase in the attraction causes the pairs to become more tightly bound, until they eventually form diatomic molecules, which are much smaller than the average separation between molecules. A molecule of two fermions behaves as a boson, the type of particle that prefers to occupy the same quantum state, hence the molecules exhibit the much lower ground-state pressure of a Bose gas. The smooth crossover from a fermionic BCS superfluid state to a molecular Bose-Einstein condensate (BEC) at low temperature has been studied extensively in recent years using ultracold atoms in three dimensions [2]. But how would such a crossover appear if the atoms are constrained to move in 2D flatland [3]? The work of Makhalov and colleagues addresses such an important and largely open question.
The BCS-BEC crossover is a general phenomenon in superfluids as well as superconductors. Although limited to the BCS side, superconductors exhibit the beginning of a crossover in materials with strong electron interactions. However, the advantage of studying ultracold atoms is that they allow the interaction strength to be tuned in a single system. This tunability comes from changing an applied magnetic field, which controls Feshbach resonances between atoms in different hyperfine states. At specific values of the magnetic field, the scattering states become resonant with a bound state of the interatomic potential, thus producing the strongest interaction allowed by quantum mechanics. It is now possible to apply a confining potential along one spatial direction (say, z), which restricts the motion of the atoms essentially to the x- y plane (see 23 January 2012 Viewpoint). This is interesting because fermions behave differently in lower dimensions and also because many solid-state materials have a layered structure as, for example, the cuprates investigated for high-temperature superconductivity.
In the new cold-atom experiment by Makhalov et al., the authors build on their previous work on atoms confined to move in two dimensions [4]. They first trap several hundred atoms in a cloud shaped like a very flat pancake (see Fig. 1). From the spatial density profile in the trap, the team can read off the pressure at the trap center as it varies with magnetic field and hence interaction strength.
These pressure measurements are the first to map out the crossover in 2D, thus providing important limits on models. Theoretically, it is far from trivial to compute the equation of state (i.e., pressure as a function of interaction strength) for a strongly interacting quantum fluid, and it is particularly challenging in 2D. The confinement in the third dimension causes strong long-range fluctuations that inhibit superfluid long-range order at nonzero temperature. In the limit of weak interaction, the pressure is just the Fermi pressure due to the Pauli principle, and it decreases slightly as the interaction strength grows. In the opposite limit of tightly bound molecules, the pressure becomes very small, as expected for a weakly repulsive Bose gas. Most interesting is thus the intermediate, strongly interacting regime, where the 2D scattering length is of the order of the particle spacing. Here, the new experiment provides the detailed crossover behavior and shows how the fermion pairs gradually turn into bosonic molecules (see Fig. 1). The pressure is measured at low temperatures in the superfluid regime and agrees with recent theoretical predictions from zero-temperature simulations [5]. On the other hand, it deviates from the naive BCS mean-field expectation of independent Cooper pairs and shows the importance of scattering between pairs. This is an example of strong coupling features, which were previously observed in the radio frequency response of a 2D atomic gas [6,7].
What are the next steps? A measurement of the equation of state and sound velocities at higher temperatures could reveal the transition temperature Tc to a normal Fermi gas and test theoretical predictions [8]. Above Tc, the tendency of fermions to form pairs leads to fewer available low-energy states up to rather high temperatures: such a pseudogap regime has been extensively discussed for high-temperature superconductors and has pronounced effects also for 2D ultracold Fermi gases [7,8]. Furthermore, the transport properties, such as the shear viscosity or diffusivity [9], of quantum fluids provide independent probes of their excitations, and it will be worthwhile to transfer 3D strong-coupling transport calculations to the 2D case.
Although this new paper shines some light onto the crossover region for a 2D quantum fluid, more experiments are needed to characterize this low-temperature phase. In a strictly homogeneous 2D Bose gas at finite temperature, no BEC with long-range order can form because of fluctuations. Instead, the system exhibits a Berezinskii-Kosterlitz-Thouless phase at low temperatures, where vortices of opposite circulation bind into pairs and correlations decay as a power law. This has been observed with ultracold bosonic atoms [10]. It will be interesting to see how this picture is modified in a quasi-2D trap and with fermionic atoms: in the future it may be possible to take snapshots of the vortices directly above and below Tc and trace their fate as the tight bosonic molecules change their character and cross over into large fermion pairs. Experiments may thus provide benchmarks for the theoretical description of strong fluctuations and shed light on some old puzzles in 2D quantum fluids, exploiting the tunability offered by ultracold atoms.
References
- Vasiliy Makhalov, Kirill Martiyanov, and Andrey Turlapov, “Ground-State Pressure of Quasi-2D Fermi and Bose Gases,” Phys. Rev. Lett. 112, 045301 (2014)
- W. Ketterle and M. Zwierlein, “Making, Probing and Understanding Ultracold Fermi Gases,” Riv. Nuovo Cimento 31, 247 (2008); I. Bloch, J. Dalibard, and W. Zwerger, “Many-Body Physics with Ultracold Gases,” Rev. Mod. Phys. 80, 885 (2008); The BCS-BEC Crossover and the Unitary Fermi Gas, Lecture Notes in Physics, Vol. 836, edited by W. Zwerger (Springer, Berlin, 2012)[Amazon][WorldCat]
- K. Miyake, “Fermi Liquid Theory of Dilute Submonolayer 3He on Thin 4He II Film Dimer Bound State and Cooper Pairs,” Prog. Theor. Phys. 69, 1794 (1983); M. Randeria, J.-M. Duan, and L.-Y. Shieh, “Bound States, Cooper Pairing, and Bose Condensation in Two Dimensions,” Phys. Rev. Lett. 62, 981 (1989); D. S. Petrov, M. A. Baranov, and G. V. Shlyapnikov, “Superfluid Transition in Quasi-Two-Dimensional Fermi Gases,” Phys. Rev. A 67, 031601 (2003)
- K. Martiyanov, V. Makhalov, and A. Turlapov, “Observation of a Two-Dimensional Fermi Gas of Atoms,” Phys. Rev. Lett. 105, 030404 (2010)
- G. Bertaina and S. Giorgini, “BCS-BEC Crossover in a Two-Dimensional Fermi Gas,” Phys. Rev. Lett. 106, 110403 (2011)
- A. T. Sommer, L. W. Cheuk, M. J. H. Ku, W. S. Bakr, and M. W. Zwierlein, “Evolution of Fermion Pairing from Three to Two Dimensions,” Phys. Rev. Lett. 108, 045302 (2012)
- M. Feld, B. Fröhlich, E. Vogt, M. Koschorreck, and M. Köhl, “Observation of a Pairing Pseudogap in a Two-Dimensional Fermi Gas,” Nature 480, 75 (2011)
- M. Bauer, M. M. Parish, and T. Enss “Universal Equation of State and Pseudogap in the Two Dimensional Fermi Gas,” arXiv:1311.1000 (2013)
- T. Enss and R. Haussmann, “Quantum Mechanical Limitations to Spin Diffusion in the Unitary Fermi Gas,” Phys. Rev. Lett. 109, 195303 (2012)
- Z. Hadzibabic, P. Krüger, M. Cheneau, B. Battelier, and J. Dalibard, “Berezinskii–Kosterlitz–Thouless Crossover in a Trapped Atomic Gas,” Nature 441, 1118 (2006)