Do Quantum Superpositions Have a Size Limit?
Everyday experience tells us that big objects—eggs and humans—do not appear to exist in a superposition of states like that possible for more quantum objects, such as electrons. Does this mean quantum physics fundamentally doesn’t apply to objects beyond a certain size? A new experiment that allows the motion of a large atom in an optical lattice to be tracked could help in the search for a size cutoff. Using this setup, Carsten Robens at the University of Bonn, Germany, and his colleagues demonstrated that a cesium atom travels in a truly nonclassical fashion, moving as a quantum superposition of states and thus occupying more than one distinct location at a time [1]. Larger objects have been observed to have such inherently quantum properties, but the observation of Robens et al. is based on a stringent test considered to be the gold standard for confirming that a superposition exists. As such, their experiment constrains theories of physics that aim to replace quantum mechanics. Their technique could also be used to test superpositions on even more macroscopic scales, such as with larger atoms or molecules.
Most experiments aiming to verify that a particle is in a quantum superposition of states look for evidence of interference. The classic experiment is to pass an electron through a pair of slits: The resultant fringes are suggestive of the wavelike behavior that quantum theory ascribes to fundamental particles. Yet even though these experiments agree with what quantum theory predicts, they aren’t foolproof tests because a classical explanation is possible: one can imagine that the electron actually goes through one slit or the other, and never through both simultaneously (as quantum physics would have it.)
In a theoretical paper in 1985, Anthony Leggett and Anupam Garg [2] approached the problem quite differently. Rather than looking to verify quantum theory, they suggested that one should instead try to rule out the alternatives by demonstrating that anything other than a quantum description led to a contradiction with experimental observation. They defined a viewpoint called macrorealism, which rests on two assumptions in conflict with quantum theory: an object of sufficiently large size is always in one place at a time (macroscopic superpositions can’t exist) and the object’s location can be determined without disturbing it. They showed that if macrorealism were true, measurements performed at different times on an object could only be statistically correlated up to a certain degree, a relation they expressed mathematically through the Leggett-Garg inequality. Experiments that indicated otherwise, i.e., that violated this inequality, would clearly show macrorealism to be false. Their work inspired a number of experiments [3] on photons [4], nuclear spins [5,6], and superconducting circuits [7].
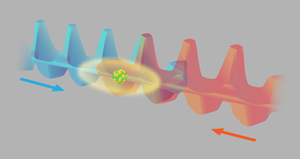
In comparison with these earlier experiments, the atoms studied in the experiments by Robens et al.’s are the largest quantum objects with which the Leggett-Garg inequality has been tested using what is called a null measurement—a “noninvasive” measurement that allows the inequality to be confirmed in the most convincing way possible. In the researchers’ experiment, a cesium atom moves in one of two standing optical waves that have opposite electric-field polarizations, and the atom’s position is measured at various times. The two standing waves can be pictured as a tiny pair of overlapping one-dimensional egg-carton strips—one red, one blue (Fig. 1). The experiment consists of measuring correlation between the atom’s position at different times. Robens et al. first put the atom into a superposition of two internal hyperfine spin states; this corresponds to being in both cartons simultaneously. Next, the team slid the two optical waves past each other, which causes the atom to smear out over a distance of up to about 2 micrometers in a motion known as a quantum walk. Finally, the authors optically excited the atom, causing it to fluoresce and reveal its location at a single site. Knowing where the atom began allows them to calculate, on average, whether the atom moved left or right from its starting position. By repeating this experiment, they can obtain correlations between the atom’s position at different times, which are the inputs into the Leggett-Garg inequality.
Now, a macrorealist would claim that the atom never started in a superposition; rather, at any given instant, it was only in the bin of one carton or the other. Furthermore she might argue that a fluorescence measurement was invasive to later measurements. Therefore, as Leggett and Garg originally proposed, Robens et al. used the “null result” measurement technique at one of the intermediate times in their experiment. In simple terms, a null measurement allows the experimenter to determine the atom’s location without directly interacting with it. To do this, the authors simply shift one of the standing waves—or cartons—by a long distance. Let’s say they shift the red carton away. If the atom fails to light up when a later fluorescence measurement is performed one knows the atom was in the red carton, was strongly interacted with, and ended up far away. Repeating this experiment, however, sometimes one finds the atom lighting up. One can then be sure the atom was in the blue carton before the shift, when the measurement was activated. Moreover, one knows that the blue carton, and therefore the cesium atom, was not tampered with.
If macrorealism described reality, a null measurement wouldn’t affect the outcome of the final fluorescence measurement, and the total amount of correlation of the atom’s position over different instances in time would be understandable without quantum mechanics. But this strikes at the heart of what makes quantum mechanics so strange. Crucially, when the atom is smeared out, as opposed to having a definite position, even null measurements have an effect. This smearing leads to a stronger total correlation than is possible under macrorealism, a fact captured mathematically by a violation of the Leggett-Garg inequality. This is precisely what Robens et al. find, and it means that macrorealism cannot apply to their cesium atom.
Almost a century after the quantum revolution in science, it’s perhaps surprising that physicists are still trying to prove the existence of superpositions. The real motivation lies in the future of theoretical physics. Fledgling theories of macrorealism may well form the basis of the next generation “upgrade” to quantum theory by setting the scale of the quantum-classical boundary. Thanks to the results of this experiment, we can be sure that the boundary cannot lie below the scale at which the cesium atom has been shown to behave like a wave. How high is this scale? A theoretical measure of macroscopicity [8] (see 18 April 2013 Synopsis) gives the cesium atom a modest ranking of 6.8, above the only other object tested with null measurements [5], but far below where most suspect the boundary lies. (Schrödinger’s cat is a 57.) In fact, matter-wave interferometry experiments have already shown interference fringes with Buckminsterfullerene molecules [9], boasting a rating as high as 12. In my opinion, however, we can be surer of the demonstration of the quantumness of the cesium atom because of the authors’ exclusion of macrorealism via null result measurements. The next step is to try these experiments with atoms of larger mass, superposed over longer time scales and separated by greater distances. This will push the envelope of macroscopicity further and reveal yet more about the nature of the relationship between the quantum and the macroworld.
This research is published in Physical Review X.
References
- Carsten Robens, Wolfgang Alt, Dieter Meschede, Clive Emary, and Andrea Alberti, “Ideal Negative Measurements in Quantum Walks Disprove Theories Based on Classical Trajectories,” Phys. Rev. X 5, 011003 (2015)
- A. J. Leggett and A. Garg, “Quantum Mechanics Versus Macroscopic Realism: Is the Flux There When Nobody Looks?,” Phys. Rev. Lett. 54, 857 (1985)
- C. Emary, N. Lambert, and F. Nori, “Leggett-Garg Inequalities,” Rep. Prog. Phys. 77, 016001 (2014)
- M. E. Goggin, M. P. Almeida, M. Barbieri, B. P. Lanyon, J. L. O’Brien, A. G. White, and G. J. Pryde, “Violation of the Leggett-Garg Inequality with Weak Measurements of Photons,” Proc. Natl. Acad. Sci. 108, 1256 (2011)
- G. C. Knee et al., “Violation of a Leggett-Garg Inequality with Ideal Non-Invasive Measurements,” Nature Commun. 3, 606 (2012)
- G. Waldherr, P. Neumann, S. F. Huelga, F. Jelezko, and J. Wrachtrup, “Violation of a Temporal Bell Inequality for Single Spins in a Diamond Defect Center,” Phys. Rev. Lett. 107, 090401 (2011)
- A. Palacios-Laloy, F. Mallet, F. Nguyen, P. Bertet, D. Vion, D. Esteve, and A. N. Korotkov, “Experimental Violation of a Bell’s Inequality in Time with Weak Measurement,” Nature Phys. 6, 442 (2010)
- S. Nimmrichter and K. Hornberger, “Macroscopicity of Mechanical Quantum Superposition States,” Phys. Rev. Lett. 110, 160403 (2013)
- K. Hornberger, S. Gerlich, H. Ulbricht, L. Hackermüller, S. Nimmrichter, I. V. Goldt, O. Boltalina, and M. Arndt, “Theory and Experimental Verification of Kapitza–Dirac–Talbot–Lau Interferometry,” New J. Phys. 11, 043032 (2009)