Some Assembly Required
Using Einstein's theory of gravity, cosmologists predict that matter should cluster into a filamentary cosmic web (see Fig. 1) whose form is strikingly similar to the observed distribution of real galaxies [1]. The observational confirmation of this prediction, and others, has given cosmologists confidence that they understand the important physics governing the large-scale distribution of mass in the Universe. However, a notable exception has been the confirmation of a long-standing theoretical prediction known as assembly bias. This notion says that the spatial distribution of objects like galaxies and galaxy clusters depends not only on the total mass of the objects, but also on the history of how they formed. A team led by Hironao Miyatake of Princeton University, and Surhud More of the Kavli Institute for the Physics and Mathematics of the Universe (IPMU), in Tokyo [2] has now measured this effect in a large number of galaxy clusters. Their measurements would, if verified by independent groups, solidify our understanding of the formation of cosmic structures and how galaxies and stars grow over cosmic time.
To understand what Miyatake et al. have measured, it is useful to review some basic facts about the large-scale distribution of mass in the cosmos. Galaxies, such as the Milky Way, are not uniformly distributed across the Universe. Instead they are clustered in space, meaning we are more likely to find a galaxy next to another galaxy than at some random point in the Universe. Clustering is expressed mathematically by the so-called galaxy correlation function, 𝜉(r). It is determined by counting the number of pairs of galaxies, with a separation r, and comparing the value to that expected from random (Poisson) statistics; unclustered galaxies would have 𝜉(r)=0. Observations confirm that 𝜉(r)>0 over distances of hundreds of millions of light years.
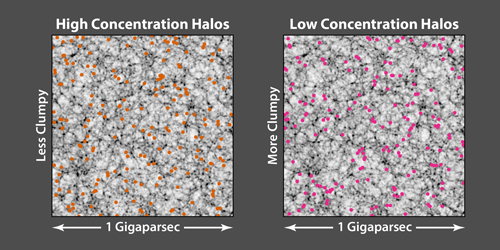
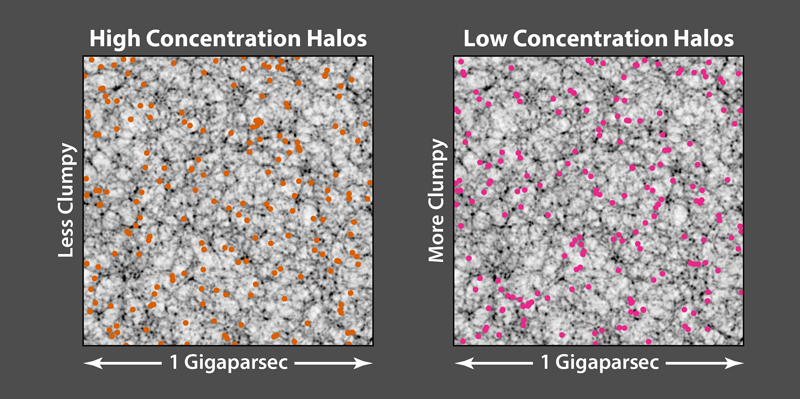
However, not all galaxies cluster in the same way. It has long been known [3] that large, massive galaxies are more strongly clustered than smaller, less massive ones. This effect, termed bias, has a simple explanation: Just as Earth’s tallest mountains are found mainly atop high plateaus like the Himalayas, so too will the Universe's highest-density peaks be found in regions where the local background density is high. These peaks are like seeds around which the most massive galaxies grow. But mass is not the only property determining spatial clustering. Both numerical simulations [4] and analytical theory [5] predict that the clustering of objects like galaxies also depends on the time it takes galaxies to form, or the rate at which they assemble. The reason for this assembly bias is that, among massive structures, the ones that are rapidly accreting tend to occur in the regions of highest density, where the mass supply is largest. They are therefore spatially clustered more strongly than objects that are growing only slowly. Assembly bias means that two galaxies with the same total mass, but distinct assembly histories, can exhibit different amounts of clustering and, therefore, different values of 𝜉(r).
The theoretical prediction of assembly bias has, unfortunately, proven surprisingly difficult to confirm observationally, despite considerable effort to do so [6]. (See note in Ref. [7].) If these nonobservations are correct, and there is no assembly bias, then scientists may need to radically rethink their cosmological theory. This might entail modifying gravitational theory, introducing new physics in the dark matter sector, or re-evaluating our understanding of density fluctuations in the early Universe. These theoretical adjustments would have to be made without wrecking the other spectacular successes of structure formation theory.
But before taking such drastic measures, researchers want to be certain they haven’t missed the effect because their measurement tools lack the precision to see it. The key difficulty is determining the masses of galaxies, which in earlier work were mostly determined indirectly, from properties like a galaxy’s brightness or color. Because spatial clustering depends so strongly on mass, even modest errors in mass determination can translate into large differences in clustering strength that can swamp the signal of assembly bias.
Miyatake et al. have circumvented this difficulty by attempting to measure assembly bias not in galaxies, but galaxy clusters, whose individual masses can be determined with greater accuracy than individual galaxies. These clusters are bound, virialized collections of hundreds or even thousands of galaxies, plus hot gas and copious amounts of dark matter. The researchers focused their study on a group of 8648 galaxy clusters, called the redMaPPer sample, from the Sloan Digital Sky Survey. The team determined the masses of the clusters by observing their distortion of the apparent shape of background galaxies, a phenomenon known as gravitational lensing. They split their sample of clusters into two groups with similar masses. One group contained slowly assembling objects, the other rapidly assembling objects. The authors determined the speed of assembly indirectly, using the fact that clusters with a high concentration of mass near their centers grow more slowly than diffusely populated clusters. (In a forthcoming work, the authors use a more direct method to distinguish the assembly rates in the two groups of clusters.) Miyatake et al. found that 𝜉(r) for the group containing rapidly assembling clusters was 2.2 times larger than the 𝜉(r) for the group containing slowly assembling clusters. This behavior resembles the assembly bias predicted by numerical simulations (Fig. 1).
The confirmation of assembly bias means that cosmologists can breathe a temporary sigh of relief. But there is a potential cloud on the horizon: the assembly bias signal measured by Miyatake et al. is somewhat larger (by less than 2𝜎) than theoretical expectations. This could be merely a statistical fluke, or it might indicate a real discrepancy with theory. Figuring this out would require a larger sample of clusters so that the effect can be determined with higher statistical significance. Similarly, cosmologists do ultimately need to determine whether the expected amount of assembly bias occurs in lower-mass objects like galaxies. The gravitational lensing method of Miyatake et al. should help in the construction of galaxy samples of known mass, which may have been the bugaboo of previous studies. In the future, we can look forward to the results of the Dark Energy Survey and the Subaru Hyper-Suprime-Cam Survey, which will dramatically increase the number of known galaxies and galaxy clusters.
This research is published in Physical Review Letters.
References
- J. R. Bond, L.. Kofman, and D. Pogosyan, “How Filaments of Galaxies are Woven into the Cosmic Web,” Nature 380, 603 (1996).
- H. Miyatake, S. More, M. Takada, D. N. Spergel, R. Mandelbaum, E. S. Rykoff, and E. Rozo, “Evidence of Halo Assembly Bias in Massive Clusters,” Phys. Rev. Lett. 116, 041301 (2016).
- N. Kaiser, “On the Spatial Correlations of Abell Clusters,” Astrophys. J. Lett. 284, L9 (1984).
- L. Gao, V. Springel, and S. D. M. White, “The Age Dependence of Halo Clustering,” Mon. Not. R. Astron. Soc.: Lett. 363, L66 (2005).
- N. Dalal, M. White, J. R. Bond, and A. Shirokov, “Halo Assembly Bias in Hierarchical Structure Formation,” Astrophys. J. 687, 12 (2008).
- Y. T. Lin, R. Mandelbaum, Y.-H. Huang, H.-J. Huang, N. Dalal, B. Diemer, H.-Y. Jian, and A. Kravtsov, “On Detecting Halo Assembly Bias with Galaxy Populations,” arXiv:1504.07632.
- Since it is difficult to observe mass growth rates directly, especially in systems where dark matter is the dominant form of mass, researchers have adopted various proxies for determining a galaxy’s formation rate. These include the rate of star formation [6], or the central concentration of mass, which previous work has shown to be related to assembly history; see R. H. Wechsler, A. R. Zentner, James S. Bullock, Andrey V. Kravtsov, and B. Allgood, “The Dependence of Halo Clustering on Halo Formation History, Concentration, and Occupation,” Astrophys. J. 652, 71 (2006).