How to Fracture a Fluid
What does it take to fracture a fluid? How hard and fast does the fluid need to be pulled in order to break? Ole Hassager, from the Technical University of Denmark, and colleagues [1] have tackled these challenging questions head-on by stretching fluids composed of polymer melts at sufficiently high strain rates to make the fluid break in the same way that a pane of glass would if pulled hard enough. The researchers found that as long as the strain rate was fast enough, fracture of the fluid followed. The overall strains that the fluids could sustain before breaking were both huge—over 250% of their initial size—and surprisingly reproducible.
Materials generally break because cracks propagate through them. The existence and size of a crack determine a material’s strength, for a crack amplifies stresses at its tip. In fact, in the classic theory of fracture, this stress amplification is unbounded—approaching a mathematical singularity. One signature of this singularity is that the crack’s branches are spread out in a parabolic form behind the crack’s tip. Crack propagation also has an energy threshold: a crack will only propagate once the elastic energy released by its extension is equal to the material’s “fracture energy,” the energy needed to create new material surface. When this threshold is exceeded, the energy flow to the stress singularity will cause the bonds at a crack’s tip to break like a chain of dominoes, breaking one after another as the crack extends through the material. This threshold translates to a value of the applied stress needed to initiate a crack’s motion, and this value depends on the crack’s length. The longer a crack, the more elastic energy is (in general) released. As a result, the energy threshold for material failure is typically determined by the “weakest link”; the largest preexisting crack or flaw in a given material determines its strength.
While this classic picture provides the general formalism for how and why materials fail, many questions remain open. These include how and at what scales nature regularizes the putative singularity at a crack’s tip, and the related question of what mechanisms determine a material’s fracture energy. A minimum value for the fracture energy is the energy necessary to break a unit area of bonds. However, in most materials, the empirical value of the fracture energy surpasses this minimal value by orders of magnitude. Recent fracture experiments have used soft materials such as aqueous gels to study fracture dynamics at reduced speeds; the propagation of fracture processes in such materials is about 1000 times slower than in standard solid materials. These studies have provided important insights into fundamental but previously inaccessible aspects of how fracture takes place. These include direct validation of a crack’s equation of motion [2] and, by enabling direct observation of the region surrounding the tip of running cracks, the opening of a window into how and where the classic picture breaks down [3, 4]. In parallel, the use of soft materials has also opened up fascinating new and rather unanticipated research directions. For example, by manipulating the internal structure of polymer gels, researchers have, in the last few years, uncovered new classes of “super-tough” materials that are orders of magnitude tougher than chemically similar polymers [5, 6].
Hassager and co-workers’ study now brings us to fracture of the “softest” of materials—viscoelastic fluids, such as polymer melts. At long time scales, these materials flow, whereas at short time scales, they behave elastically as the entangled polymer strands within the fluid resist motion, stretching instead of sliding past one another. In a fluid, one would not intuitively expect to see a crack at all. One would certainly not expect to discern mesoscopic flaws or initial cracks that determine the macroscopic strength of a solid, because surface tension would quickly close them. How, then, can fluids fracture, as the present study has shown?
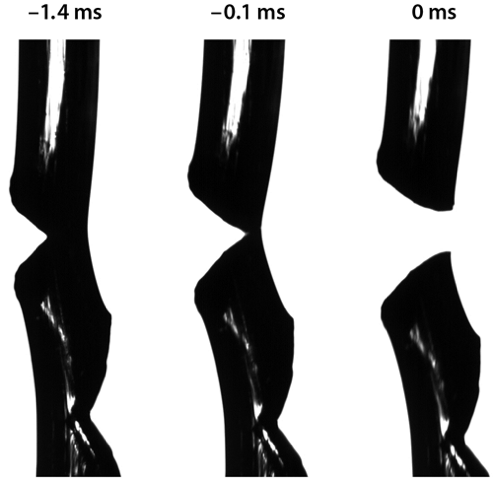
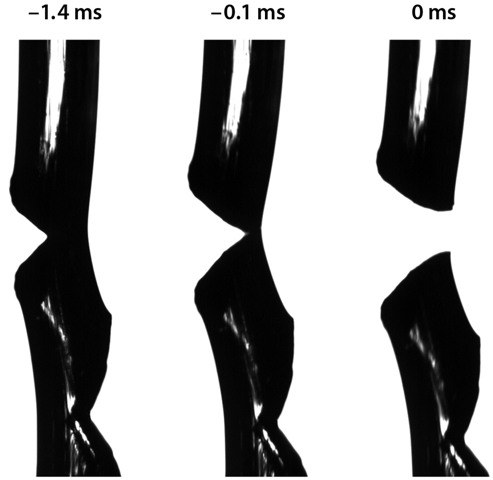
The authors’ work demonstrates that viscoelastic fluids, in a sense, may approach their ultimate strength prior to fracture. By pulling columns of fluids sufficiently rapidly, the authors demonstrated with high-speed imaging (Fig. 1) that the strains attained when the fluid columns fractured were extreme, with values comparable to the maximal observed strains in the vicinity of moving crack tips in soft materials [7]. In strong contrast to solid materials, the critical strains for material failure were highly reproducible, suggesting that a mechanism other than the “weakest link” controls the stress attained by the material at failure. Moreover, the observation of simultaneous fracture at two different spatial points is nearly impossible in a “weakest link” scenario. Adopting ideas proposed by Yves Pomeau in the early 1990s [8], the authors explain these observations by considering thermally activated cracks, which appear via thermal fluctuations—not preexisting flaws.
But are the observed fracture events really cracks? As previously observed in a so-called Maxwell fluid [9], the propagating cracks in the polymer melts studied here possess the classic parabolic shape at small scales that is expected by fracture theory, reinforcing the idea that dynamic fracture mechanics dominates the material’s behavior at failure. In addition, at length and time scales at which the fluid’s viscous motion is not effectively frozen out, Hassager and co-workers’ study demonstrated that the classic fracture picture crosses over to a characteristic behavior first predicted by Pierre-Gilles de Gennes [10], in which the viscous response of the material dominates the elastic response.
What are the implications of this study? The idea of soft materials has challenged our classic notions of fluid and solid materials. Experiments such as these manifestly demonstrate that processes such as brittle fracture that are innately related to solids can indeed take place in fluid-like materials. This work is an interesting example of how externally imposed time scales (for example, strain rate) can qualitatively affect material behavior. It will be interesting to see how properties that characterize the fracture process (for example, the fracture energy) can be quantitatively related to both the viscous and elastic properties of soft materials, and how these might be used to manipulate material strengths and macroscopic properties such as material elasticity [11].
This research is published in Physical Review Letters.
References
- Q. Huang, N. J. Alvarez, A. Shabbir, and O. Hassager, “Multiple Cracks Propagate Simultaneously in Polymer Liquids in Tension,” Phys. Rev. Lett. 117, 087801 (2016).
- T. Goldman, A. Livne, and J. Fineberg, “Acquisition of Inertia by a Moving Crack,” Phys. Rev. Lett. 104, 114301 (2010).
- E. Bouchbinder, T. Goldman, and J. Fineberg, “The Dynamics of Rapid Fracture: Instabilities, Nonlinearities and Length Scales,” Rep. Prog. Phys. 77, 046501 (2014).
- R. Long and C.-Y. Hui, “Crack Tip Fields in Soft Elastic Solids Subjected to Large Quasi-Static Deformation — A Review,” Extreme Mech. Lett. 4, 131 (2015).
- J. P. Gong, “Why are Double Network Hydrogels so Tough?,” Soft Matter 6, 2583 (2010).
- C. Creton and M. Ciccotti, “Fracture and Adhesion of Soft Materials: A Review,” Rep. Prog. Phys. 79, 046601 (2016).
- A. Livne, E. Bouchbinder, I. Svetlizky, and J. Fineberg, “The Near-Tip Fields of Fast Cracks,” Science 327, 1359 (2010).
- Y. Pomeau, “Brisure Spontanée de Cristaux Bidimensionnels Courbés,” C. R. Acad. Sci. Paris II 314, 553 (1992).
- H. Tabuteau, S. Mora, M. Ciccotti, C. Hui, and C. Ligoure, “Propagation of a Brittle Fracture in a Viscoelastic Fluid,” Soft Matter 7, 9474 (2011).
- P. G. de Gennes, “Soft Adhesives,” Langmuir 12, 4497 (1996).
- S. Xia, L. Ponson, G. Ravichandran, and K. Bhattacharya, “Toughening and Asymmetry in Peeling of Heterogeneous Adhesives,” Phys. Rev. Lett. 108, 196101 (2012).