A New Way to Channel Light
Light hitting a surface exerts a tiny pressure. Ordinarily these forces have little effect, but a report in Physical Review Letters describes theoretically how radiation pressure can be harnessed to make light traveling through narrow glass “strips” focus itself into beams. The system works for any wavelength and provides a new technique for shaping and controlling light.
In many new devices, light signals are replacing electronic signals, so researchers are looking to extend their abilities to control light on small scales. Anna Butsch of the Max Planck Institute for the Science of Light in Erlangen, Germany, and her colleagues analyzed the behavior of light traveling through two thin flat glass sheets placed parallel to each other, apart. They could be two long strips inside a cable that could carry light signals. The strips in their analysis ranged in thickness from to , were wide, and were rigidly fixed in place at their edges.
Although light traveling down the dual-strip structure is concentrated within the strips, electromagnetic radiation also spreads out into the gap between the strips as well as above and below them. This external field exerts a small pressure on the strips, pushing them either together or apart. The calculated bending is small—only one or two nanometers of displacement for the modest light intensities assumed in the analysis—but it is enough to affect light propagation within the strips. Butsch and her colleagues describe the change in terms of an effective refractive index that varies across the width of the strip according to the degree of bending. As a result, light no longer travels uniformly within the entire width of the strip, but in essence focuses itself into one or more narrow tracks.
This behavior follows from a straightforward application of classical electromagnetic theory, coupled with knowledge of the elastic properties of the glass. Writing down the relevant equations is easy, but solving them is not. Bending of the strips causes a complicated feedback because pressure applied to a strip at one point or along one line creates curvature throughout the strip, which influences the propagation of light everywhere within it. This in turn changes the optical pressure that bends the strips in the first place.
The team used an iterative process to find solutions. They assumed an initial pressure profile across the strips, calculated the resulting bending, radiation pattern, and pressure, and then repeated the cycle. In most cases, within ten or fewer iterations, they found convergence, meaning a stable solution in which the propagation pattern of light was consistent with the resulting bending of the strips.
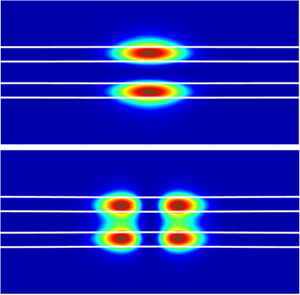
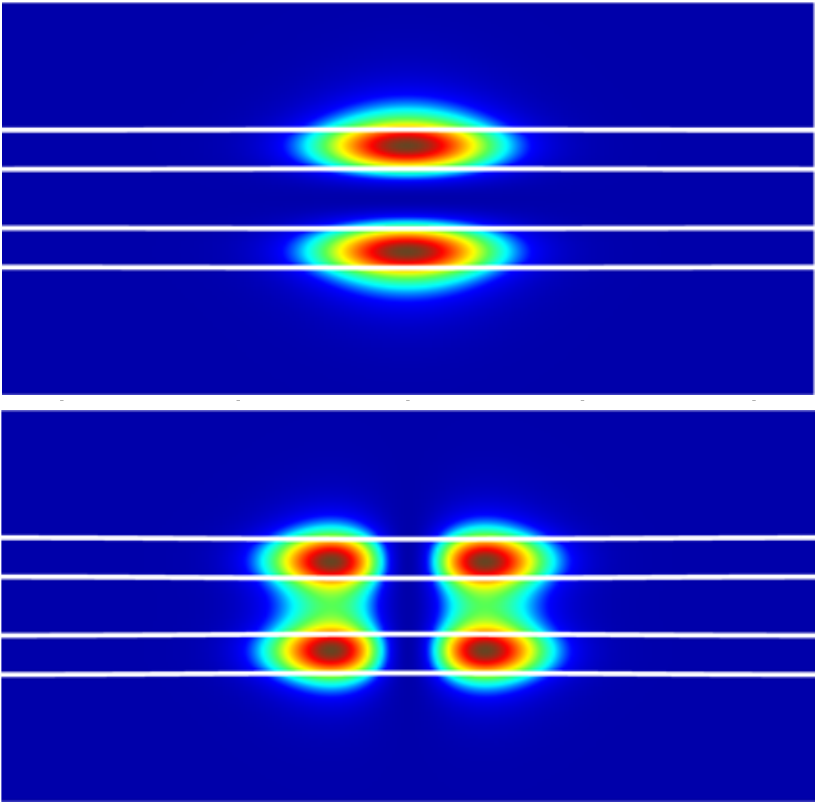
A variety of possible patterns emerged, with light confined by the self-focusing mechanism to one or two tracks within each of the two strips. When they allowed the thicknesses of the two strips to be different, they obtained asymmetric solutions, with a more intense beam in one sheet and a weaker one in the other.
Although this work is purely theoretical, the team says that such a system should be easy to make and would allow beams to travel distances of several meters. And because the effect does not involve any sort of resonance phenomena, it will work for light of any wavelength. Different modes of confinement (numbers of beams) would be excited by shaping the initial light pulse applied to the strips, which could allow finer degrees of control over the light signals.
Mo Li of the University of Minnesota in Minneapolis calls the study “an exciting theoretical prediction of a novel nonlinear optical effect.” He says it could lead to “breakthroughs in ultrafast optics and optical metrology.” Butsch and her colleagues are now studying more complex possibilities, including interactions between different modes that might be useful in switching or other applications.
–David Lindley
David Lindley is a freelance science writer in Alexandria, Virginia.