Quantum Information Not Lost in Translation
Physicists hoping to make an ultrapowerful quantum computer still haven’t settled on which quantum system to build it out of. In Physical Review Letters, a team proposes a way to faithfully transfer quantum information back and forth between two of the candidates—a single trapped ion and a superconducting circuit. If the scheme works out, it could allow researchers to explore hybrid technologies that combine the strengths of these two different quantum entities.
A simple quantum system can effectively be in two states simultaneously. When scaled up to many similar systems working in parallel, this property allows a huge amount of computational power, at least in theory. But there is not yet a clear winner among several possible building blocks to represent the individual quantum bits, or “qubits,” of quantum information. Each type of qubit has strengths and weaknesses, so researchers have recently been proposing hybrids. For example, an ion floating in an electromagnetic trap can retain its quantum state long enough to allow many sequential operations, but it’s complicated to engineer the required interactions between different ions. In contrast, the quantized electromagnetic oscillations in superconducting circuits are easier to manipulate using the complex wiring capabilities of modern microelectronics, but extending their lifetimes has been difficult. David Kielpinski of Griffith University in Nathan, Australia, and his collaborators now suggest a way to enmesh the quantum behavior of a circuit with that of an ion, to let each do what it does best.
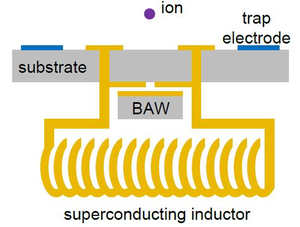
Both the circuit and the ion reveal their quantum nature when a particular mode of oscillation is just barely excited. For the circuit, this mode is the familiar voltage and current oscillation of an circuit, whose frequency depends on its inductance ( ) and its capacitance ( ). For the ion, the researchers chose its relatively long-distance motion (tens of nanometers) back and forth inside an electromagnetic trap. The problem is that the typical oscillation frequencies are so different—the ion in the megahertz range and the circuit in the gigahertz range—so it’s hard to get them to communicate.
To bridge this thousandfold frequency gap, Kielpinski and his collaborators propose adding another electrical signal whose frequency precisely matches the difference. Mixing two signals to form a new signal at the sum or difference of their frequencies is widely used, for example, to encode audio signals for radio broadcasts. The challenge in this case is to preserve the delicate quantum information, which would be destroyed by simply irradiating an ion and circuit with a large microwave signal. To avoid this, the team proposes varying the parameters of the circuit at the required frequency, using a so-called bulk acoustic wave (BAW) to vibrate one of the plates of the capacitor in the circuit. Varying the capacitance would vary the resonant frequency of the circuit, and the combination signal would provide a megahertz-range electric field that would influence the ion’s motion.
The team calculates that, using existing technology and a well-designed circuit, experimenters could alter the capacitance by as much as percent, enough to generate a large signal that would match the ion frequency. Applying the BAW signal for just the right amount of time would then controllably swap the quantum states of the jiggling ion and the oscillating circuit.
If it works, one use of the new scheme would be to “let quantum information from superconducting circuits escape from the dilution refrigerator” that keeps them at ultralow temperatures, says Kielpinski. He imagines fiber-optic lines carrying quantum information between two distant circuits, with trapped ions as the intermediary technology between the optical and electronic signals. The team also proposes using the superconducting circuit to ferry quantum information between ions, perhaps allowing their interaction to be better controlled than if the two ions were placed in the same trap for a multi-ion calculation.
“An interface that connects different systems … can only help with the attempt to produce the optimal hardware,” says Steve Girvin of Yale University in New Haven, Connecticut. But he cautions that “some of these experiments are hard separately and hard-squared collectively.” Jose Aumentado of the National Institute of Standards and Technology in Boulder, Colorado, agrees that the proposal “looks really challenging, if it could be built.” But experiments on other systems have shown that quantum states can be swapped without adding noise, he says. “Parametric frequency conversion is super-important.”
–Don Monroe
Don Monroe is a freelance science writer in Murray Hill, New Jersey.
More Information
How to Catch a Moonbeam (Focus, 2000)
commentary by Steve Girvin on lifetimes in superconducting qubits (Condensed Matter Journal Club, 2012)