The Physics of Loners

JR Minkel

Focus

The Physics of Loners

September 3, 2002• Phys. Rev. Focus 10, 10

Condensed matter physics could offer insights into human cooperation.

Figure caption — **It’s all a game.** When simulated on a lattice, a game theory model of human cooperation goes through distinct phases. Each player is represented by a pixel colored according to its strategy at the moment: cooperator (blue), defector (red), or loner (yellow).

Physics might help bring people together, claims a pair of physicists. Researchers studying a “public goods game, ” a simple model of cooperation, believe that allowing players the option to drop out of competition makes teamwork more likely to persist among those who remain. Now the team, publishing in the 9 September print issue of PRL, finds that a spatially extended version of this scenario exhibits phase transitions and traveling waves, suggesting that condensed matter physics might help elucidate aspects of human cooperation.

In trying to understand the dynamics of cooperation among humans or animals, some researchers look to simple game theory models. These are computer-run scenarios where a group of “players” is given a set of choices, each with prescribed consequences. In a typical public goods game (PGG), individuals receive a fixed amount of money at the start of every round and can either place it in a communal pot or keep it. At the end of each round, the pot is doubled (if the “interest rate” is 100%) and split among the players. If everyone contributes, they all double their money. If exactly one defects, that player receives more than double. Depending on the game parameters, players may prefer to keep their money rather than risk that others will defect.

Christoph Hauert, now at the University of British Columbia in Vancouver, and his collaborators, proposed that such stingy behavior could be ameliorated by introducing a third strategy: Risk averse loners could drop out of the game altogether and forego the cash to eke out a small but dependable income by themselves [1]. They found that loners allowed cooperators to survive over a broader range of parameters but didn’t study a spatially extended game in detail.

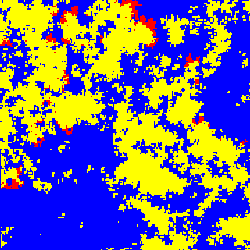
Now Hauert and György Szabó, of Budapest’s Research Institute for Technical Physics and Materials Science, have found that when played on a lattice, where points are colored according to the players’ strategies, the voluntary PGG generates phase transitions and traveling waves. Each player, corresponding to one pixel, plays with four neighbors and occasionally reassesses its strategy by comparing its score with the performance of its neighbors. As the interest rate rises, loners dominate completely at first, then coexist with the other two types, and finally die out, leaving large clusters of cooperators spread among defectors. In the middle phase, cooperators form traveling waves that are eroded on one side by new defectors and built up on the other by converted loners.

These properties resemble those of the Ising model of magnetism and directed percolation models, used for example to analyze the way fluids move through a porous medium, say the authors. Solid-state physics offers tools that might yield new game theory insights, Hauert says, which in turn might help derive measures to increase cooperation. “But humans are complicated beings,” he adds, and this limits concrete applications of model results.

The paper supports the idea that cellular automata, or simple computer simulations, could serve as flexible tools in a range of fields, says Karl Sigmund of the University of Vienna. Sigmund, who worked with Hauert in developing the loner concept, points out that the strategies of players in the PGG are very complex because they depend not only on what their neighbors are doing, but also on the neighbors of those neighbors. And yet they show the same patterns as relatively simple physical models. “This points to a remarkable universality,” he says.

–JR Minkel

JR Minkel is a freelance science writer in New York City.