Breaking time reversal symmetry with light
Physics has at its essence the study of the symmetries observed in nature, and these symmetries, in turn, give rise to conservation laws and the properties of particles. Yet these symmetries are not enough, for without the breaking of symmetries there would not be a universe that could observe them. Among the most important of these symmetries is time reversal—breaking this symmetry leads to a variety of interesting physical effects, especially in condensed matter physics. In a paper in Physical Review A, Jens Koch, Karyn Le Hur, and Steven Girvin at Yale University, and Andrew Houck at Princeton University [1], both in the US, report their design for an elegant photonic circuit that demonstrates this phenomenon, enabling new tests of strongly correlated condensed matter physics.
What is so special about time reversal with photons? It is the basis behind the Sagnac effect, where rotation breaks the symmetry between clockwise and counterclockwise propagating optical fields in an otherwise symmetric interferometer [2]. Sagnac interferometers already find great application as laser gyroscopes. Alternatively, for a modest fee, anyone can purchase a device that breaks time-reversal symmetry for light without rotation. This device is called an optical isolator and is an integral part of many laser systems to prevent stray reflections causing deleterious feedback to the laser. Optical isolators work by employing a Faraday rotator that rotates the polarization of a beam of light in a direction parallel to an applied magnetic field, which in turn implies that forward and backward propagating fields pick up polarization rotations in opposite senses. What has not been proposed before is a lattice of such rotators. The physics that comes out from this system is very interesting indeed. Breaking time-reversal symmetry can be thought of as introducing both a fictitious charge for the photons, and a synthetic electromagnetic field to which this charge reacts. This allows the photonic system to emulate the integer and fractional quantum Hall effects.
Typically, the quantum Hall effect is observed in two-dimensional electron gases: atomically perfect interfaces in aluminum gallium-arsenide heterostructures. In these devices, the time-reversal symmetry breaking occurs due to a magnetic field applied perpendicular to the two-dimensional electron gas. The energy levels of the quantized electron orbits take on discrete values: Landau levels. For strong magnetic fields each Landau level is highly degenerate. In this regime, when the Fermi energy of the two-dimensional electron gas falls between two Landau levels, the Hall resistance is quantized in units of . This is the integer quantum Hall effect [3]. This analysis breaks down when the electron-electron interactions play a significant role, leading to the fractional quantum Hall effect [4,5]. Our understanding of the fractional states is based on exact many-body quantum mechanical solutions for a small number of electrons and trial wave functions for the many-body ground state, leading to a fractionally charged, anyonic, quasiparticle description.
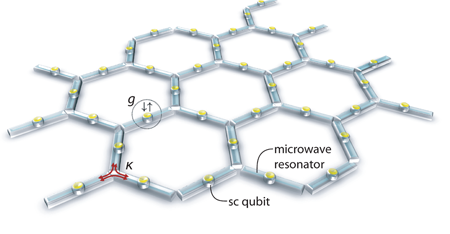
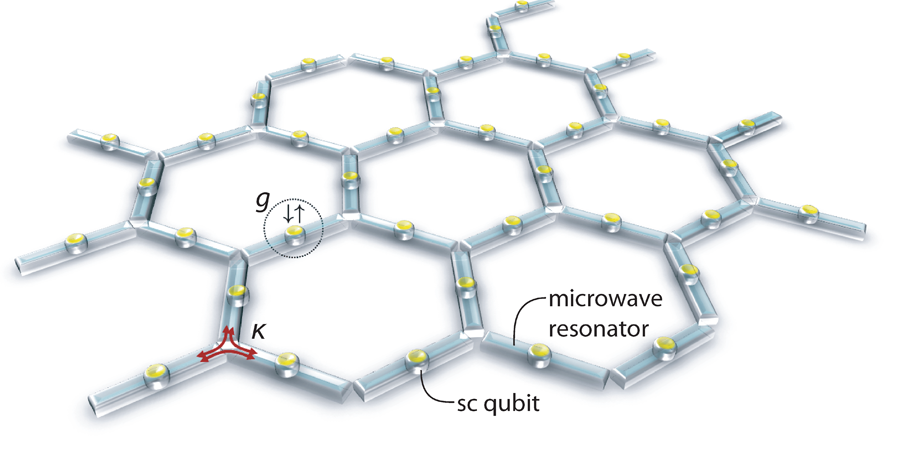
Koch et al. have combined the ideas of photonic lattices and time-reversal symmetry to design a new form of quantum simulator, ideally suited to exploring quantum Hall physics with light (Fig. 1). A photonic lattice of this type [6–8] constitutes a vision for a new kind of condensed matter system. It describes a lattice of interacting atom-cavity (Jaynes-Cummings) systems, where photon hopping (for example, via evanescent coupling) provides a Hubbard-type model, and on-site interactions are mediated by the atom-photon coupling. The Hubbard model is one of the canonical foundations of condensed matter physics, used in the study of superconductivity and other correlated systems. It is now well accepted that the Jaynes-Cummings-Hubbard lattice will exhibit a metal-insulator phase transition, and there has been considerable effort in exploring extensions and mappings of this to other condensed matter models. The major advantage of a photonic lattice over other competing simulators is that it provides unique opportunities for local control and readout of the quantum state of individual constituent elements. In the optical regime, advances in optical nanofabrication are expected to allow sufficiently large numbers of individual elements to explore thermodynamic properties. In the microwave regime explored by Koch et al., tunability of circuit elements is the advance necessary to access large-scale systems. Irrespective of the frequency range, breaking time-reversal symmetry will open an entirely new class of condensed matter to study with light.
Accessing the time-reversal symmetry breaking in a photonic lattice is difficult. In a Sagnac interferometer, the phase difference between the counter-propagating paths is proportional to the area of the individual loops times the rotation frequency. This implies that very large angular velocities are required for measureable phase shifts in micro-optical structures. Cho, Angelakis, and Bose described a more practical foray into quantum Hall physics with a photonic lattice in 2008 [9]. They proposed a two-dimensional (square) lattice of cavities, each containing an isolated three-level atom. The orthogonal directions have different resonant wavelengths and control of the phases of pump lasers provides the appropriate symmetry-breaking mechanism.
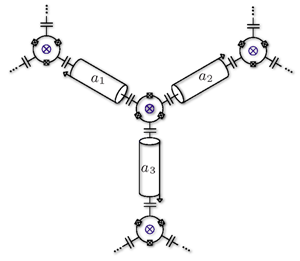
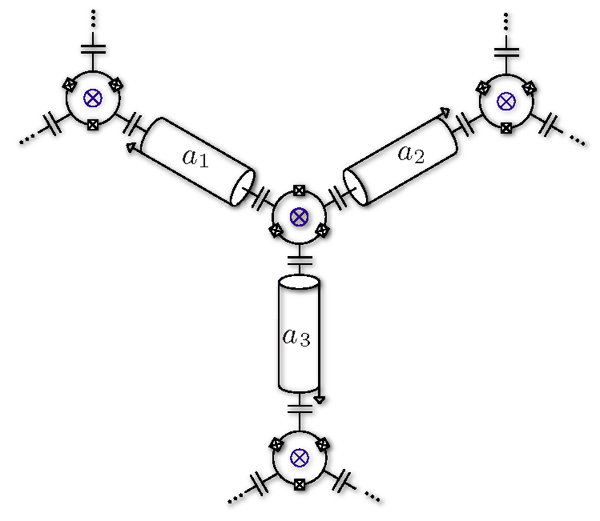
The method for symmetry breaking used by Koch et al. is quite different. Here they consider a circulator, a device functionally similar to the optical isolator described above. This multiport device will tend to circulate photons in a sense defined by an external magnetic field. By connecting atom-cavity systems—in this case defined by superconducting qubits in microwave resonators—via circulators, rather than just tunnel junctions, a definite chirality to the photon hopping is ensured. This chirality, combined with a graphite lattice of atom-cavity systems, generates a kagome lattice. This latter innovation allows new possibilities including interaction-induced topological phases and tunable band structures.
Building a photonic lattice with circulators might be feasible, but as the authors point out, the large size of commercial ferrite circulators (on the centimeter scale) compared to microwave resonator cavities, places severe constraints on the design. What is required is an on-chip solution compatible with lithographic techniques. One means of breaking time-reversal symmetry for charged particles is the Aharonov-Bohm effect. A particle with the possibility of following two paths, which enclose a vector potential, will feel a different phase shift for each path, dependent on the enclosed flux. In a similar fashion, the authors show that a three-junction Josephson ring enclosing a flux can act as an on-chip circulator (Fig. 2), although care is required to tune the circuit so that symmetry breaking can occur. Fabrication of such a structure appears entirely compatible with conventional lithography, and hence one would expect that a working quantum emulator is not far behind.
Emulation of fractional quantum Hall states will offer significant new insight into the fundamental properties of these strongly correlated states. This has led to significant interest in the generation of synthetic electromagnetic fields in quantum degenerate gases [10–13]. The work of Koch and co-workers [1] provides the toolbox for building a new class of photonic lattice quantum Hall emulators. As in the case of quantum degenerate gases, this lattice will enable direct probing of the many-body correlated states, as the quantum state of each cavity can be read independently. Specifically, this will allow the investigation of synthetic electromagnetic fields in the photonic lattice, where the interactions between the photons can be tuned. For example, in the photon Mott-insulator regime, the play off between the photon repulsion and a synthetic magnetic field may lead to strongly correlated many-body states that have strong analogies to the many-body states responsible for the fractional quantum Hall effect observed in two-dimensional electron gases.
Acknowledgments
The authors thank Andrew Hayward from the University of Melbourne for useful discussions.
References
- J. Koch, A. A. Houck, K. Hur, and S. M. Girvin, Phys. Rev. A 82, 043811 (2010)
- G. E. Stedman, M. T. Johnsson, Z. Li, C. H. Rowe, and H. R. Bilger, Opt. Lett. 20, 324 (1995)
- K. von Klitzing, G. Dorda, and M. Pepper, Phys. Rev. Lett. 45, 494 (1980)
- D. C. Tsui, H. L. Stormer, and A. C. Gossard, Phys. Rev. Lett. 48, 1559 (1982)
- R. B. Laughlin, Phys. Rev. Lett. 50, 1395 (1983)
- M. J. Hartmann, F. G. S. L. Brandão, and M. B. Plenio, Nature Phys. 2, 849 (2006)
- A. D. Greentree, C. Tahan, J. H. Cole, and L. C. L. Hollenberg, Nature Phys. 2, 856 (2006)
- D. G. Angelakis, M. F. Santos, and S. Bose, Phys. Rev. A 76, 031805(R) (2007)
- J. Cho, D. G. Angelakis, and S. Bose, Phys. Rev. Lett 101, 246809 (2008)
- I. B. Spielman, Phys. Rev. A 79, 063613 (2009)
- Y.-J. Lin, R. L. Compton, K. Jiménez-Garcia, J. V. Porto, and I. B. Spielman, Nature 462, 628 (2009)
- P. Zoller and D. Jaksch, New J. Phys. 5, 56 (2003)
- F. Gerbier and J. Dalibard, New J. Phys. 12, 033007 (2010)