Vanquishing infinity
Gravity is different. It is mediated by particles (gravitons) of spin 2, unlike the other known forces in nature (electromagnetism and the strong and weak interactions), which are carried by particles of spin 1. This explains why like gravitational charges (that is, masses) attract, whereas in electrostatics, like charges repel, thereby accounting for the fact that gravity dominates physics at large distances, despite its incredible weakness in comparison with the other fundamental forces (think of a little magnet whose force on a safety pin beats the gravitational pull of the whole planet Earth). Modern understanding of gravity rests on Einstein’s theory of general relativity. This theory is based on the principle of general covariance (according to which, the laws of physics should not depend on which coordinate system is used to formulate them) and the principle of equivalence, enabling Einstein to write down “in one stroke” his gravitational field equations and thereby to revolutionize our understanding of gravity, replacing Newtonian gravity by a theory based on spacetime geometry and curvature.
There is another key aspect in which gravity differs. Matter is governed by the laws of quantum mechanics, but so far, Einstein’s theory has resisted all attempts to reconcile it with quantum mechanics. Our understanding of subatomic phenomena is encoded in the standard model of elementary particle physics (based on an extension of quantum electrodynamics called Yang-Mills theory) which, for all we know, correctly describes the interactions of known matter within relativistic quantum field theory. This is an elaborate mathematical framework, which took many decades to develop and still presents many difficulties. These are due in particular to the necessity of having to deal with infinite expressions appearing at intermediate stages of every calculation, and their removal by a procedure referred to as renormalization. Infinities generally arise because of the pointlike nature of elementary particles, implying short distance singularities in the formulas (or “ultraviolet infinities” in momentum space). To this day we are not sure whether quantum field theory makes sense as a mathematical theory, but we do know that it works exceedingly well in perturbation theory, yielding spectacular agreement between theory and experiment. However, applying the established rules of quantum field theory to Einstein gravity and its generalizations results in complete failure—with one possible exception: As Zvi Bern, John Carrasco, and Henrik Johanssen at UCLA, Lance Dixon at the Stanford Linear Accelerator Center, and Radu Roiban at Pennsylvania State University, all in the US, report in Physical Review Letters, supergravity, distinguished among all other field theories by its maximal supersymmetry, may evade this dilemma [1].
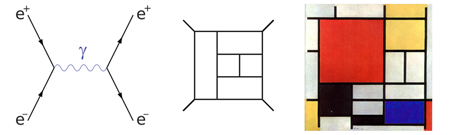
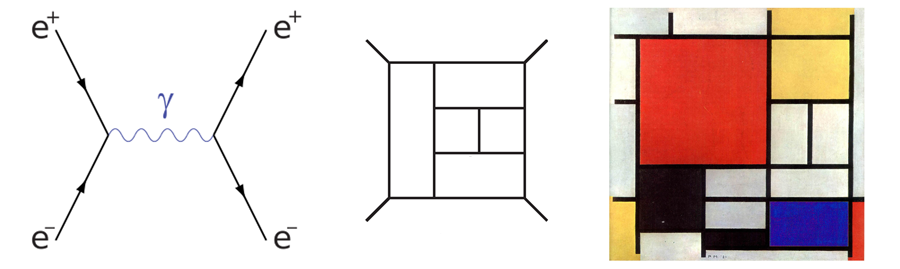
The inconsistencies of perturbatively quantized gravity appear in the form of nonrenormalizable infinities. This means that in order to remove the divergent expressions resulting from standard Feynman diagram (Fig. 1) computations, one must modify the Einstein equations by new types of interactions (counterterms) involving higher and higher powers of the curvature tensor at each order in perturbation theory—unlike for renormalizable matter interactions, where infinite renormalizations are only necessary for a finite number of parameters (masses and coupling constants), but no new types of interactions are needed. As a consequence, one must specify an infinite number of parameters and couplings if one wants finite results to any given order. But such a theory has no predictivity whatsoever, because every physical prediction would depend on an infinity of parameters. Any hopes that miraculous cancellations might prevent this disaster for pure gravity were shattered by an impressive calculation [2,3].
In the late 1970s physicists set out to find an extension of Einstein’s theory that would be free of ultraviolet (UV) infinities. The idea was to modify gravity by the inclusion of matter couplings finely tuned to cancel the infinities (and thereby perhaps also identify a raison d’être for the existence of matter in the world). First of all this requires fermionic matter, because fermions contribute with a relative minus sign from bosons for each closed loop inside a Feynman diagram. In addition, the requisite extension of Einstein’s theory must possess a new type of symmetry—local supersymmetry—relating bosons and fermions, and thus forces and matter particles. It was soon realized that such supersymmetric extensions of Einstein’s theory become rarer and rarer with increasing number of supersymmetries . The maximally supersymmetric extension of Einstein’s theory, supergravity, was finally constructed in Ref. [4] and, in its more general “gauged” version, in Ref. [5].
Naturally, these developments raised hopes that supergravity was at last the looked-for theory that would tame the infinities of perturbatively quantized Einstein gravity. A brief period of intense activity followed to find out whether this theory might actually be finite to all orders. These investigations were mostly based on superspace, an extension of spacetime by fermionic coordinates [6]. Unfortunately, when applied to supergravity, this method has a major drawback: it works only at the level of the equations of motion, but does not allow setting up a scheme for computing Feynman diagrams. The outcome of all these efforts, then, was disappointingly inconclusive. After much work, it was shown in Refs. [7,8] that there do exist counterterms compatible with supersymmetry. However, because of the lack of a workable off-shell formalism, no one was able to calculate the coefficients of the relevant counterterms (the first of which appears at three loops [9]) and thereby definitely rule them in or out. Most researchers therefore concluded that the theory was doomed, in line with the rule of thumb that an infinity that cannot be excluded by symmetry arguments actually does appear with a nonvanishing coefficient (just like the two-loop counterterm for pure gravity [2,3]). Many turned to superstring theory, which appeared to offer much better prospects for constructing a perturbatively finite theory of quantum gravity and for explaining the observed features of low-energy particle physics from a unified theory. As a result, a general conviction took hold that the issue of UV finiteness of supergravity was not only hopelessly difficult to settle once and for all, but more importantly, not a truly relevant question anymore. And so it might well have languished forever in the no man’s land of undecidable propositions, had it not been for the recent progress reported by Bern et al. [1].
To understand why an approach based on standard Feynman diagram techniques is so forbiddingly complicated, let us recall two simple facts. First, the particles circulating in Feynman diagrams are off-shell, that is, they do not obey the usual relativistic dispersion relation . Secondly, in order to keep Lorentz invariance manifest, one must sum not only over physical polarizations, but also over a host of unphysical excitations (for instance, in QED the photon is described by a four vector , and thus comes with four polarizations instead of just the two physical helicities). For gravity, calculational complexity increases enormously: the calculation [2,3] involves hundreds of thousands of Feynman diagrams. A cursory glance at the Lagrangian [4,5] will probably suffice to dissuade anyone from even trying to think about doing the calculation in this way!
The progress that started the long march towards the computation of Bern et al. [1] originally grew out of attempts to simplify the computation of multiparticle scattering amplitudes in particle physics, and QCD in particular. A main novelty of this approach was to bring in string theory in an essential way, consistently exploiting the fact that quantum field theory amplitudes can be derived by taking special limits of string amplitudes (where the string degenerates to a point). The latter often turn out to be “easier” to calculate, precisely because their computation does not involve unphysical intermediate states. As a crucial further ingredient [10], this program revived methods from an old approach to particle physics (going by the name of S-matrix theory) that had flourished in the 1960s.
To extend these considerations to gravity required the ingenious exploitation of another key feature of string theory. String theory describes massless spin-1 and spin-2 particles as excitations of open and closed strings, respectively. In the computation of amplitudes this feature is mirrored in the fact that on-shell gravity amplitudes can be obtained by “squaring” on-shell Yang-Mills amplitudes; the precise recipe for doing this was devised by Kawai, Lewellen, and Tye—the KLT rules [11]. String theory can thus substantiate the idea that gravity is, in some sense, the “square” of Yang-Mills theory. Despite its obvious appeal and simplicity, however, the idea goes much deeper: no amount of fiddling with the Einstein-Hilbert action (which is nonpolynomial) will reduce it to the square of a Yang-Mills action. To bring the crucial factorization property out into the light of the day, much more work is required [12]. In fact, to understand how that happens one better forget just about everything one has learnt in quantum field theory textbooks!
More specifically, the method employed in [1] proceeds by “gluing” on-shell amplitudes of yet another prominent supersymmetric theory: Yang-Mills theory. Being UV finite and exactly conformal, it is a very rare specimen in the zoo of quantum field theory models. The gluing technique thus permits one to build the finiteness properties of Yang-Mills theory into the calculation of the gravity amplitudes right from the start, thereby saving a lot of sweat (which is still needed in other places). However, putting together all the pieces that culminated in the calculation of Bern et al. [1] took more than ten years of hard work, and we cannot even begin to describe here the bag of tricks required to carry it to successful completion. Still, and quite amazingly, in the end the whole calculation can be reduced to the computation of about 50 scalar four-loop integrals involving only cubic vertices. All these diagrams must conspire to give the requisite cancellations and the finite end result.
To be sure, these results do not yet constitute a proof that supergravity is truly a perturbatively finite theory of quantum gravity (nor can they be easily generalized to gauged supergravity). Nevertheless, the computation of Bern et al. [1] actually goes much farther than would be needed to establish the stated finiteness result, in that it also supplies subleading contributions (in fact, the Feynman integrands) rather than just the finite value of the integral. All these results indicate that finiteness will persist to yet higher orders. Before contemplating a five-loop computation, however, it is perhaps time now to search for a deeper underlying reason that might possibly explain finiteness. Many suspect that this reason has something to do with an as yet undiscovered symmetry of supergravity, and, in fact, a symmetry beyond maximal supersymmetry. Indeed, there is one obvious candidate, namely the “hidden” symmetry called discovered long ago by Cremmer and Julia [4]. Reconciling known on-shell counterterms with this symmetry remains a thorny problem, but it is most doubtful whether alone can do the job of explaining finiteness. There are yet larger (infinite dimensional) hidden symmetries of exceptional type in maximal supergravities that might eventually become relevant here, but this remains a speculation for the moment.
In a wider perspective, what do these results mean for superstring theory and its claim to be the sole pretender to the throne of a perturbatively consistent extension of Einstein’s theory? String theory differs from field theory in that, on top of its pointlike excitations, it has an infinite tower of massive states corresponding to the quantized vibrational modes of the string. However, a closer look reveals that its (still conjectural) finiteness hinges not so much on the presence of these extra states, but rather on a new type of symmetry (called modular invariance), which has no field theory analog. This suggests that the new symmetry that may ultimately explain finiteness must act in a way very different from known realizations of spacetime and internal symmetries. Accordingly, we should view the coexistence of several possibly finite candidate theories only as a first step towards the future construction of an underlying theory of quantum gravity, where classical space and time are only emergent concepts, and which would also be viable nonperturbatively. At present we are still far from having such a theory, but Ref. [1] will surely remain as a milestone in this ongoing search. It is a stunning achievement.
References
- Z. Bern, J. J. M. Carrasco, L. J. Dixon, H. Johansson, and R. Roiban, Phys. Rev. Lett. 103, 081301 (2009)
- M. H. Goroff and A. Sagnotti, Nucl. Phys. B 266, 709 (1986)
- A. van de Ven, Nucl. Phys. B 378, 309 (1992)
- E. Cremmer and B. Julia, Nucl. Phys. B 159, 141 (1979)
- B. de Wit and H. Nicolai, Nucl. Phys. B 208, 323 (1982)
- L. Brink and P. S. Howe, Phys. Lett. B 88, 81 (1979)
- R. E. Kallosh, Phys. Lett. B 99, 122 (1981)
- P. S. Howe, K. S. Stelle, and P. K. Townsend, Nucl. Phys. B 191, 445 (1981)
- S. Deser, J. H. Kay, and K. S.Stelle, Phys. Rev. Lett. 38, 527 (1977)
- Z. Bern, L. J. Dixon, D. C. Dunbar, and D. A. Kosower, Nucl. Phys. B 425, 217 (1994)
- H. Kawai, D. C. Lewellen, and S. H. Tye, Nucl. Phys. B 269, 1 (1986)
- Z. Bern, Living Rev. Relativity 5, 5 (2002); http://www.livingreviews.org/lrr-2002-5
- Z. Bern, J. J. M. Carrasco, H. Johansson, and D. A. Kosower, Phys. Rev. D 76, 125020 (2007)