Flipping a photonic shock wave
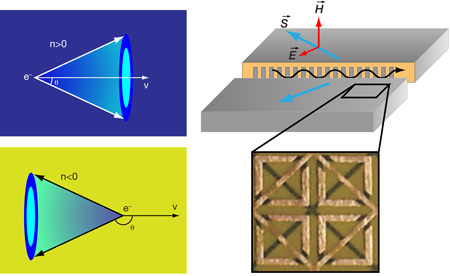
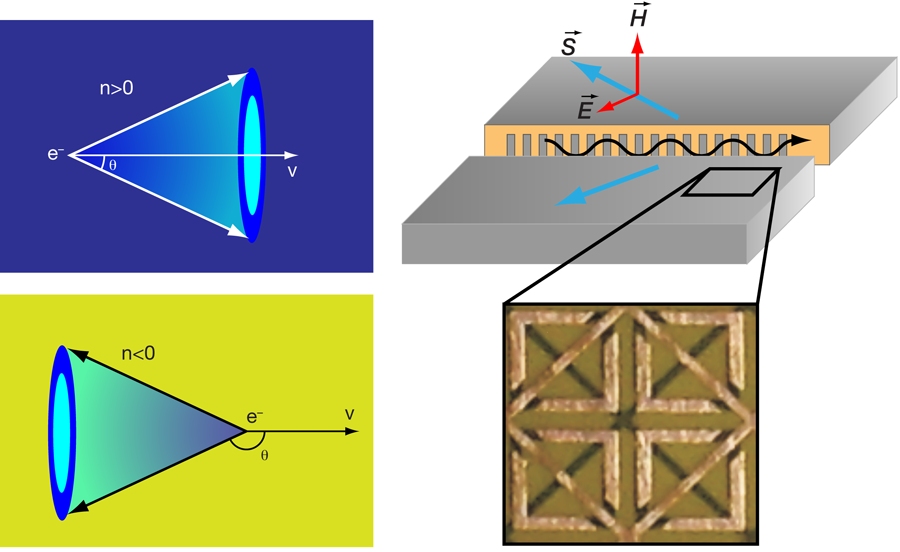
When charged particles such as electrons travel through a dielectric medium with a speed greater than the phase velocity of the light in the medium, electromagnetic radiation is emitted that falls into a cone fanning out in the forward direction [Fig. 1, top left]. This phenomenon is called Čerenkov radiation, named after the Russian scientist who first characterized it rigorously and was awarded the Nobel Prize in Physics in 1958. Most people are familiar with Čerenkov radiation from the blue glow of an underwater nuclear reactor as it emits energetic charged particles. The angle of the Čerenkov emission cone is related in a simple way to the particle velocity. This unique feature enables a wide range of applications, from the measurement of fast particles in high-energy physics, the characterization of fission rate in nuclear reactors, to the detection of labeled biomolecules. Now in a paper appearing in Physical Review Letters, Sheng Xi and colleagues at Zhejiang University, China, and the Massachusetts Institute of Technology, US, experimentally demonstrate that the direction of the cone of Čerenkov radiation can be reversed in artificially engineered composite media, namely, metamaterials [1].
Backward Čerenkov radiation is one among a number of other unusual phenomena associated with so called left-handed materials, first proposed by Victor Veselago in 1968 [2]. A left-handed medium has simultaneous negative permittivity and negative permeability . In such a medium, the electric field, magnetic field, and wave vector form a left-handed triad, in contrast to the “right-hand rule” in natural materials known so far, such as water and glass. As a result, the direction of the advancing phase (the wave vector of the electromagnetic wave) is opposite to its energy flow (or Poynting vector) and the phase index of refraction is negative. The exotic phenomena in a left-handed medium include negative refraction, inverse Doppler effect, backward Čerenkov radiation, and negative radiation pressure, as predicted by Veselago more than forty years ago.
The deduction for backward Čerenkov radiation in a left-handed medium is straightforward. The half angle of the Čerenkov radiation cone is determined by the ratio between the phase velocity of the light and the particle speed as , where and are the phase velocity of the electromagnetic wave and the particle speed in the medium, respectively. Since the phase velocity in a left-handed medium is negative, i.e., opposite to the direction of the energy flow, the cone angle is obtuse and hence the radiation cone is facing toward the backward direction [Fig.1, bottom left].
While exhibiting very interesting features, media with negative refractive index are not found in nature. Thanks to the discoveries by Pendry and others about a decade ago, composite materials with effective negative refractive index have been realized [3,4], which are called metamaterials. Negative index metamaterials normally consist of two types of functional elements: “split-ring resonators” with a negative magnetic response and thin metal wires with a negative electric response. This opens the door to the testing of some of those unconventional phenomena proposed by Veselago. Many groups around the world have routinely observed a negative refractive angle at the interface between a positive index medium and a negative index metamaterial [3,5]. There have also been a few experiments exhibiting the inverse Doppler effect [6].
There have been a few studies in the past to investigate the Čerenkov radiation in left-handed metamaterials, but a convincing experimental demonstration of reversed Čerenkov radiation turns out to be challenging. This is largely due to the fact that the Čerenkov radiation power peaks in the ultraviolet region of the spectrum, where negative index metamaterials are not currently available. The Čerenkov radiation power falls off rapidly at longer wavelength and becomes extremely weak at microwave frequencies (where the technologies for the fabrication of metamaterials are very mature). In a recent study, Antipov et al. at the Illinois Institute of Technology observed microwave radiation when a charged particle beam was directed through a waveguide loaded with negative index metamaterials operating in the microwave frequency range [7]. The spectrum of the radiation exhibited a peak at the same frequency as the left-handed band of the metamaterial, providing some evidence of Čerenkov radiation in the negative index medium. However, the propagation direction of the radiation could not be determined conclusively, thus backward Čerenkov radiation was not observed in their study.
The successful demonstration of backward Čerenkov radiation by Xi et al. largely relied on two key experimental innovations. The first is a novel negative index metamaterial design, which operates for electromagnetic waves with the magnetic field component perpendicular to the plane of wave propagation in the two-dimensional experimental setting [Fig. 1, right]. Until now, most of the negative index metamaterials were designed for waves with out-of-plane electric field, so the electromagnetic wave can be confined simply by two parallel metal plates. However, this configuration is not suitable for the investigation of Čerenkov radiation since the electric field of Čerenkov radiation lies in the plane formed by the particle trajectory and the radiation wave vector. In this work, Xi et al. develop a new design in which both the split-ring resonators and metal wires are in-plane. This configuration works for the electromagnetic waves that have in-plane electric field (along the wires) and out-of-plane magnetic field (perpendicular to the split-ring resonators). It also allows an isotropic propagation of the electromagnetic waves in the metamaterials and thus makes it possible to determine the direction of Čerenkov radiation.
The second innovation is to emulate a charged-particle beam by means of a waveguide with a periodic array of slots, instead of using real charged particles [Fig. 1, right]. By doing so, Xi et al. solved the problem of extremely weak Čerenkov radiation in the microwave frequencies associated with moving charged particles. As an electromagnetic wave travels inside the waveguide, it emerges at each slot with a fixed phase retardation relative to the neighboring slots. This leaking radiation from the waveguide is equivalent to the radiation from a phased antenna array. The Fourier transform of the electric current carried by a moving charged particle results in a broad spectrum in the frequency domain. But as long as a single frequency is concerned, the current of the charged particle is equivalent to that of a phased dipole array, as mathematically proved by the authors. In this analog, the phase velocity of the electromagnetic wave propagating inside the waveguide corresponds to the moving speed of the charged particles in a regular Čerenkov radiation configuration.
In the experiment, the authors designed a waveguide with comparatively low refractive index of , which is equivalent to a charged particle moving with a speed twice as great as that of light in a vacuum. With this new experimental configuration, the radiation signal can be many orders of magnitude stronger than the traditional Čerenkov radiation induced by a fast charged-particle beam, and thus the Čerenkov radiation was directly observed along the backward direction within the left-handed frequency range of the metamaterials. It is worth noting that Grbic and Eleftheriades carried out an experimental attempt earlier at the University of Toronto, in which they observed the backward radiation from a low-index left-handed microwave transmission line into free space [8]. However, considering the fact that it is the phase velocity rather than group velocity of the electromagnetic wave propagating in the transmission line that corresponds to the speed of an equivalent moving charge, the Čerenkov radiation observed by Grbic et al. was indeed in the forward direction with respect to the direction of the equivalent moving charge.
From one point of view, the experiment by Xi et al. could be considered as a special case of negative refraction, in which the light is negatively refracted from a low positive index medium (or waveguide) to a high negative index medium at a grazing incident angle. This alternative view highlights the intrinsic connection between the phenomena of backward Čerenkov radiation and negative refraction. This should be of no surprise, however, since both phenomena are coherent processes involving a phase matching condition along a certain direction. On the other hand, a more direct demonstration of backward Čerenkov radiation with charged particles passing through a left handed metamaterial may be highly desirable for the purpose of both fundamental investigations and practical applications, such as detectors. In the last several years, the negative index metamaterials have been extended from microwave frequencies to terahertz [9], infrared, and even optical frequencies [10–12], where the Čerenkov radiation is expected to be orders of magnitude more intense than that at the microwave frequencies. In particular, the recent realization of bulk negative index optical metamaterials may offer us the opportunity to observe backward Čerenkov radiation of actual moving charged particles in the foreseeable future [13].
Acknowledgments
Support from US Army Research Office ARO MURI program 50432-PH-MUR is acknowledged.
References
- S. Xi, H. Chen, T. Jiang, L. Ran, J. Huangfu, B-I. Wu, J. A. Kong, and M. Chen, Phys. Rev. Lett. 103, 194801 (2009)
- V. G. Veselago, Soviet Physics Uspekhi 10, 509 (1968)
- J. B. Pendry et al., IEEE Trans. Microwave Theory Tech. 47, 2075 (1999)
- R. A. Shelby, D. R. Smith, and S. Schultz, Science 292, 77 (2002)
- A. A. Houck, J. B. Brock, and I. L. Chuang, Phys. Rev. Lett. 90, 137401 (2003)
- N. Seddon and T. Bearpark, Science, 302, 5650 (2003)10.1126/science.1089342
- S. Antipov et al., J. Appl. Phys. 104, 014901 (2008)
- A. Grbic and G. V. Eleftheriades, J. Appl. Phys. 92, 5930 (2002)
- T. J. Yen, W. J. Padilla, N. Fang, D. C. Vier, D. R. Smith, J. B. Pendry, D. N. Basov, and X. Zhang, Science 303, 1494 (2004)
- S. Zhang, W. Fan, N. C. Panoiu, K. J. Malloy, R. M. Osgood, and S. R. J. Brueck, Phys. Rev. Lett. 95, 137404 (2005)
- V. M. Shalaev, W. Cai, U. K. Chettiar, H-K. Yuan, A. K. Sarychev, V. P. Drachev, and A. V. Kildishev, Opt. Lett. 30, 3356 (2005)
- G. Dolling, G. M. Wegener, C. M. Soukoulis, and S. Linden, Opt. Lett. 32, 53 (2007)
- J. Valentine, S. Zhang, T. Zentgraf, E. Ulin-Avila, D. A. Genov, G. Bartal, and X. Zhang, Nature 455, 376 (2008)