Wiring Up Displacement Currents
Realizing that conduction currents couldn’t sufficiently explain the behavior of capacitors, Maxwell postulated the existence of displacement currents and changed the face of electromagnetics forever. Conduction currents ( ) involve the transport of “free” electrical charges, and in Ampere’s law ( ) they are the sole source of curled magnetic fields. Maxwell realized that time-varying displacement fields ( ) are also a form of current ( ). His correction to Ampere’s law underpins the electromagnetic wave phenomena central to photonics and befuddles physicists who work in high-speed electronics. As microchip engineers try to cram greater numbers of faster wires into smaller volumes, for instance, inevitable and undesired displacement currents leech power, generate cross talk, and distort the delicate timings within circuits [1]. Can displacement currents be corralled with the level of ease associated with conventional low-frequency wiring? In a paper in Physical Review Letters, Brian Edwards and Nader Engheta from the University of Pennsylvania, Philadelphia, take a serious step in this direction with an experimental demonstration of displacement current wiring [2] (see also the authors’ video abstract).
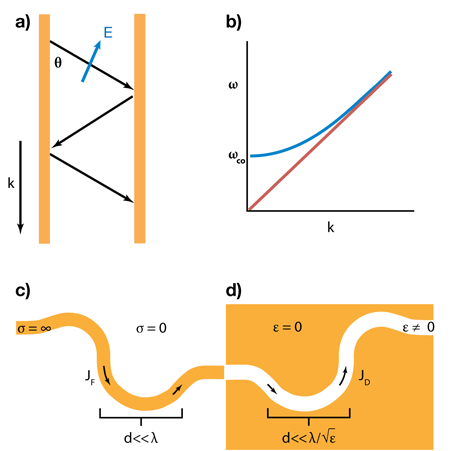
From an electrodynamics perspective, highly conducting wires act as waveguides that transmit transverse electromagnetic waves [Fig. 1(a), (b)]. At frequencies of a few megahertz, the wavelength of one of these photons ( ) is significantly larger than the dimensions of a circuit board. Thus, the current passing each point along continuous wiring has identical phase, as expected from electrostatics. Although the fields, stored energy, and power are all confined to the dielectric cladding that surrounds these wires, the cladding’s lack of conductivity ensures that the currents are confined within the metallic wires [Fig. 1(c)]. As frequency increases, the wavelength of electrical signals goes down and the current can acquire a phase across the dimensions of a typical circuit. At the same time, the conductivity of typical metals decreases while the displacement current, which is proportional to ( ), increases in magnitude and significance. At optical frequencies, the provenance of photonics, displacement current is the dominant term in the curl equation ( ), and wavelengths are comparable to feature sizes in a modern computer circuit.
In 2007, Engheta and co-workers proposed a method for wiring up displacement currents using a class of new and unusual materials with zero permittivity. Just as conventional wires confine current because the insulating sheath has zero conductivity, these “epsilon-near-zero (ENZ)” materials cannot conduct displacement currents, and finite-epsilon channels embedded within these materials act like displacement current wires [Fig. 1(d)] [3]. The analogies with conventional wiring don’t end there. In an ENZ wire, the electric fields are purely transverse within the ENZ cladding but longitudinal within the finite-epsilon core—resulting in a longitudinal displacement current. Currents propagate along the wires with a wavelength close to that of a photon traveling within the cladding, which approaches infinity for an ENZ material [3]. These properties can be exploited to wire ultrahigh frequency circuit elements [4] together in a manner analogous with electrostatics [5].
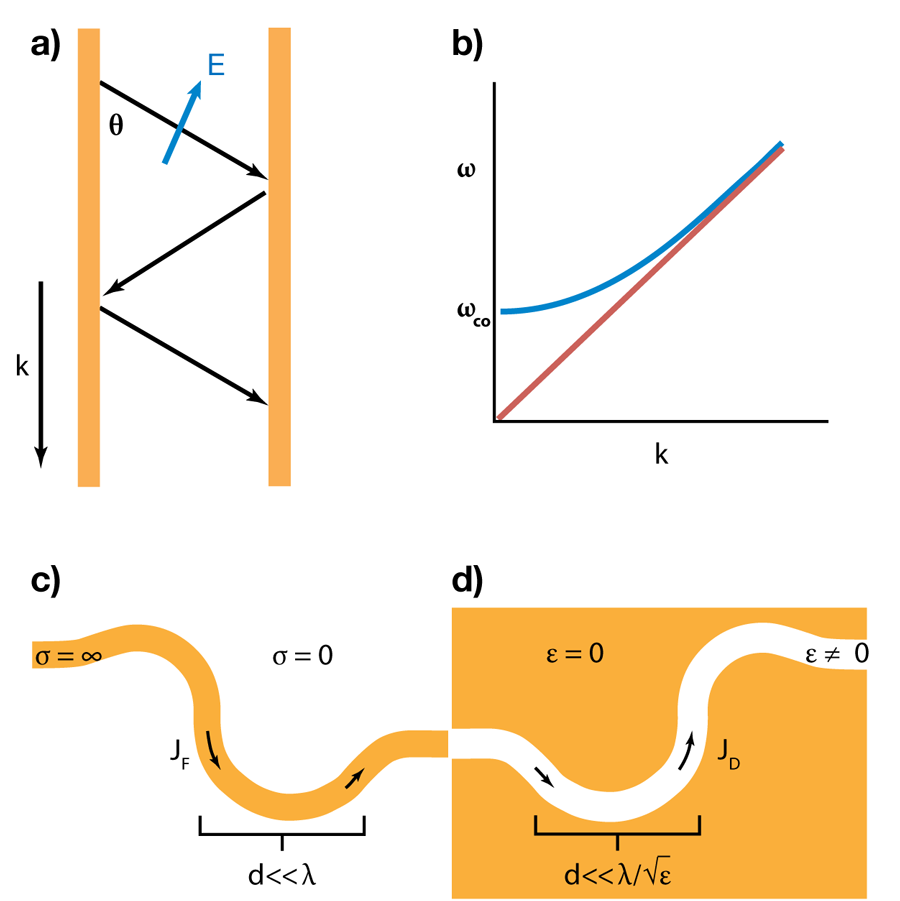
Where can one get an ENZ material? Ionic solids and covalent semiconductors exhibit ENZ properties at their longitudinal optical phonon frequency and, similarly, metals and ionized gases at their plasma frequency [6]. Because these are intrinsic material’s properties, there is little room to engineer the operating frequency of a homogeneous ENZ medium. Instead, Edwards and Engheta exploit the properties of metal-clad microwave waveguides to mimic the behavior of an ENZ material. At sufficiently high frequencies, higher order modes can travel between two perfectly conducting metal slabs [Fig. 1(a)]. The dispersion relation for one of these modes is shown in Fig. 1(b) (blue curve). The dispersion is functionally identical to that of a wave propagating in a plasma. In both instances the dispersion curves are linear at large and intersect the axis (i.e., where and ) at a finite frequency. In metals, this is the plasma frequency ( ), and the permittivity is zero. In the waveguide, this is the design frequency where the waveguide can be engineered to behave as if its permittivity were effectively zero. At this cutoff frequency ( ), the light rays bouncing back and forth within the metal slabs approach a bounce angle of . Consequently, the effective wavelength approaches infinity ( ) and the electric fields become predominantly longitudinal ( ).
Edwards and Engheta design a similar microwave waveguide, with a dielectric polymer slab sandwiched between two brass plates. They show that displacement current flows longitudinally along their structure, advancing in phase by less than radians over a distance of multiple free-space wavelengths. Even in the presence of a severe bend, the displacement current remains nicely guided along the wire. In electrostatic circuits, currents must always complete a closed loop by eventually returning to ground. The same is true of these displacement-current conduits. Edwards and Engheta show that their waveguide has a positive effective permittivity within the dielectric slab and a negative effective permittivity in the surrounding air regions; displacement currents flow along the dielectric slab in one direction and return through air in the opposite direction. The ENZ properties of the waveguide arise from a spatial average of the effective permittivity, which equals zero at their design frequency.
Ultimately, the technological realization of displacement current wiring may hinge on practical concerns such as losses and available bandwidth. Edwards and Engheta nicely demonstrate an inherent tradeoff between losses and ENZ behavior in their wires. At frequencies above cutoff, their waveguide losses decrease rapidly while the wave vector approaches that in free space ( ). At frequencies below cutoff, the wave vector approaches zero ( ), but the waveguide becomes lossier. Within a narrow frequency range near cutoff they show that both the wave vector and losses can be close to zero. Although this bandwidth is small in their wires, Edwards and Engheta argue that large ENZ bandwidths may be obtained at optical frequencies. In a weakly damped ( ) Lorentz oscillator, for instance, the bandwidth over which the permittivity is close to zero is proportional to the plasma frequency ( ). Using metal-based metamaterials [7,8], ENZ properties can be engineered at desired optical frequencies, although losses are inevitable. Dielectric metamaterials [9,10] and zero- photonic crystals [11], on the other hand, can be constructed from constituents with nearly zero intrinsic dissipation. These systems may allow physicists to study the inherent relationship between losses and effective medium properties [12] of ENZ materials, and ultimately lead to nearly lossless ENZ materials. The work of Edwards and Engheta highlights an interesting area of study for physicists who study the propagation of light and currents from microwave to ultraviolet frequencies.
References
- A. Deutsch et al., Proc. IEEE 89, 529 (2001)
- B. Edwards and N. Engheta, Phys. Rev. Lett. 108, 193902 (2012)
- A. Alù and N. Engheta, Opt. Express 15, 13773 (2007)
- N. Engheta, A. Salandrino, and A. Alù, Phys. Rev. Lett. 95, 095504 (2005)
- A. Alù and N. Engheta, Phys. Rev. Lett. 103, 143902 (2009)
- N. W. Ashcroft and N. D. Mermin, Solid State Physics (Harcourt, Orlando, 1976)[Amazon][WorldCat]
- J. B. Pendry, A. J. Holden, W. J. Stewart, and I. Youngs, Phys. Rev. Lett. 76, 4773 (1996)
- H. N. S. Krishnamoorthy, Z. Jacob, E. Narimanov, and I. Kretzschmar, and V. Menon, Science 336, 205 (2012)
- Q. Zhao, J. Zhou, F. Zhang, and D. Lippens, Mater. Today 12, 60 (2009)
- J. A. Schuller, R. Zia, T. Taubner, and M. L. Brongersma, Phys. Rev. Lett. 99, 107401 (2007)
- S. Kocaman et al., Nature Photon. 5, 499 (2011)
- M. W. McCall, J. Mod. Opt. 56, 1727 (2009)