Searching high and low for bottomonium

Stephen Godfrey

Viewpoint

Searching high and low for bottomonium

Ottawa-Carleton Institute for Physics, Department of Physics, Carleton University, Ottawa, Canada K1S 5B6

August 11, 2008• Physics 1, 11

The BABAR collaboration at SLAC has observed the radiative decay of an excited state of bottomonium (the bound state of a bottom quark and its antiparticle) to its ground state

η_{b}

. Observing this long-sought ground state should enable better tests of quantum chromodynamic calculations of quark interactions and the computational approach called lattice quantum chromodynamics.

Figure caption — **Figure 1:** (Top) The $b \bar{b}$ spectrum showing electromagnetic transitions between levels. The states that have been observed are labeled with masses taken from the Particle Data Book [16] and unobserved states are shown unlabelled with masses given by Godfrey and Isgur [9]. The unlabeled arrows show electric dipole transitions and the labeled transition (green arrow) is the $M 1$ transition observed by the BABAR collaboration in their discovery of the $η_{b}$ . The dashed line indicates the threshold above which $b \bar{b}$ will have large decay rate to $B - \bar{B}$ final states. (Bottom) The inclusive photon spectrum observed by BABAR is shown, including the background components (green, blue) that must be subtracted to obtain the $η_{b}$ signal (red) [3].

Just over thirty years ago, a new generation of quarks was discovered when Fermilab announced they had found the bottom quark [1], adding to the known up, down, strange, and charm quarks. The discovery was indirect—the actual detection involved finding bottom-antibottom quark pairs ( $b \bar{b}$ ) that form bound states via strong interactions and have a rich spectroscopy analogous to that of the hydrogen atom [2]. These composite particles are called bottomonium, an analogy to the well-known electron-positron pairs called positronium. The first two $b \bar{b}$ states that were discovered are named upsilon particles ( $Υ$ and $Υ'$ ) and were found in 1977 during experiments with collisions of 400-GeV protons on nuclear targets at Fermilab [1]. Subsequently, a variety of other excited states (all spin triplets) have been observed.

However, no spin-singlet state had been seen until the observation of the ground state called $η_{b}$ , now reported in Physical Review Letters [3] by the BABAR collaboration. The difference in mass between the $Υ$ and the $η_{b}$ is important in understanding quark-antiquark states (generally called quarkonia) by testing existing models, the applicability of perturbative quantum chromodynamics to the $b \bar{b}$ system, and the results of the numerical approach, known as lattice quantum chromodynamics (lattice QCD), to calculate hadron properties [4]. More importantly, having a measured value will challenge theorists to perform more precise calculations that can be compared to experiment.

Heavy quarkonia, which are bound states of a heavy quark and antiquark, are well described by nonrelativistic potential models originally derived to describe charm-anticharm ( $c \bar{c}$ ) states [5,6]. The potentials incorporate general features of quantum chromodynamics (QCD)—the theory of quarks and gluons describing the strong interactions. At short distances, these QCD-motivated potentials take the form of a one-gluon exchange potential, analogous to the photon exchange that is responsible for the Coulomb interaction in quantum electrodynamics (QED). Added to this are relativistic corrections, such as spin-spin and spin-orbit terms, all with “color” factors reflecting the more complicated group structure of QCD compared to QED. The spin-spin term, for example, is analogous to the hyperfine interaction that gives rise to the 21-cm line in hydrogen. At large separation the potential is described by a linearly rising interaction that confines the quarks. The QCD-motivated phenomenological potential is in good agreement with results obtained using numerical lattice-QCD methods [4]. Lattice QCD is a nonperturbative approach that deals with the nonlinear nature of the strong interaction by dividing space and time into discrete grid points and then integrating over quark and gluon configurations.

In these potential models, quarkonium energy levels are found by solving a nonrelativistic Schrödinger equation, although more sophisticated calculations take into account relativistic corrections [7]. The calculations yield energy levels that are characterized by the radial quantum number $n$ , which is equal to one plus the number of nodes of the radial wave function, and $L$ , the relative orbital angular momentum between the quark and antiquark. In fact, much of the nomenclature is familiar from atomic physics. The orbital levels are labeled by $S$ , $P$ , $D$ (corresponding to $L = 0, 1, 2$ ). The spins of the quark and antiquark couple to give total spin $S = 0$ (spin-singlet) or $S = 1$ (spin-triplet) states. $S$ and $L$ couple to give the total angular momentum of the state $J$ , which can take on values $J = L - 1$ , $L$ , or $L + 1$ . Thus the $L = 0$ states are $^{1} S_{0}$ and $^{3} S_{1}$ ; the $L = 1$ states are $^{1} P_{1}$ and $^{3} P_{0}$ , $^{3} P_{1}$ , $^{3} P_{2}$ , etc.

In addition to the spin-independent potential, there are spin-dependent interactions that give rise to splittings within multiplets [7]. With these, we can predict $Υ - η_{b}$ splittings in bottomonium and similar splittings in charmonium that are analogous to the hyperfine splittings in hydrogen. Splittings within $P$ -wave and higher $L$ -state multiplets are due to spin-orbit and spin-spin interactions arising from one-gluon exchange and a relativistic spin-orbit precession term. The contact spin-spin splitting between the singlet and triplet $P$ -wave states is predicted to be small due to its short range and because the wavefunction at the origin for $P$ -wave states is zero.

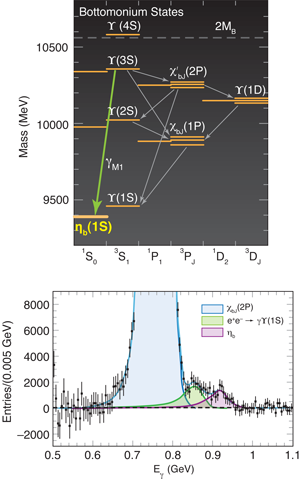
The observations of the $η_{b}$ by BABAR [3] and the charmonium state $h_{c}$ by CLEO [8] are important validations of this picture. In the experiment reported by Aubert et al., electrons and positrons from the PEP-II storage ring at SLAC collide with a center-of-mass energy of 10.355 GeV. This energy is selected so that the collisions create $Υ (3 S)$ particles, some of which then decay radiatively to the $η_{b} (1 S)$ state. Figure 1 shows the $b \bar{b}$ spectrum of observed states along with predictions for missing states [9] by Isgur and myself. The commonly used names of observed levels are shown. Note that $b \bar{b}$ states with mass greater than two times the mass of a $B$ meson (the ground state of a meson made up of a bottom-quark and a light up or down quark), will have a large decay rate into $B - \bar{B}$ pairs so the branching ratio for radiative decays will be small.

Electromagnetic transitions between the levels can be calculated in the quark model and provide an important tool in understanding the quarkonium internal structure [10]. The theory and terminology of electromagnetic transitions between quarkonium states closely follows the treatment given for transitions in the hydrogen atom in undergraduate quantum mechanics textbooks with the replacement of the electric charge of the electron with that of the quark charge and one has to include both the quark and antiquark transition amplitudes. The leading-order transition amplitudes are due to electric dipole transitions ( $E 1$ ) between states with the same total spin and magnetic dipole transitions ( $M 1$ ) which flip the quark or antiquark spin and are inversely proportional to the constituent quark mass. The predictions for $E 1$ transitions, $^{3} P_{J} \leftrightarrow^{3} S_{1}$ , in the bottomonium system are in good agreement with experimental data [10]. Recently, the CLEO experiment observed a $1 D$ bottomonium state in a cascade of $E 1$ transitions with a mass of $10161.1 \pm 0.6 \pm 1.6 MeV / c^{2}$ [11], which is in good agreement with theoretical predictions [7].

In the nonrelativistic limit the spatial overlap integrals for $M 1$ transitions equal one between $S$ -wave states within the same multiplet (that is, they are favored transitions) and zero for transitions between states with different radial quantum numbers (that is, these transitions are hindered). Relativistic corrections leads to small overlaps for these hindered transitions, which can be compensated by large phase-space factors [12]. Until the observation of the hindered $Υ (3 S)$ to $η_{b}$ transition, no $M 1$ transitions had been observed in the bottomonium system.

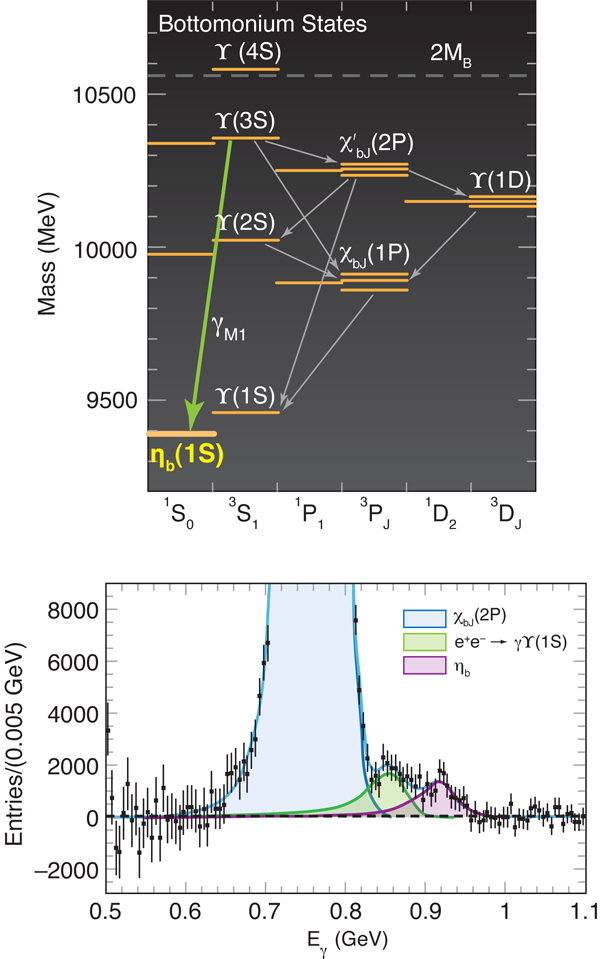
Until now, all of the observed states in the bottomonium system were spin-triplet states but quark models predict the existence of spin-singlet partners including the ground state. As mentioned above, while the decay amplitudes for hindered transitions are much smaller than those for favored transitions, this can be compensated with the larger available phase space in transitions such as $Υ (3 S) \to η_{b} (1 S)$ . BABAR collected a large data set by tuning the $e^{+} e^{-}$ energy to the mass of the $Υ (3 S)$ and observed a signal in the photon energy with $E_{γ} = 921.2 + 2.1 / - 2.8 (stat) \pm 2.4 (syst) MeV$ where the first error is statistical and the second systematic, which they interpreted as an $M 1$ transition to the $η_{b} (1 S)$ [3]. This corresponds to an $η_{b} (1 S)$ mass of $9388.9 + 3.1 / - 2.3 (stat) \pm 2.7 (syst) MeV / c^{2}$ with corresponding $Υ (1 S) - η_{b}$ hyperfine mass splitting of $71.4 + 2.3 / - 3.1 (stat) \pm 2.7 (syst) MeV / c^{2}$ .

The measured $Υ (3 S) - η_{b}$ splitting is consistent with potential model predictions although a significant subset of predictions lie outside experimental one-sigma error bounds [12]. A recent lattice-QCD calculation predicts a value of $61 \pm 14 MeV / c^{2}$ , which is consistent within the large errors [4]. Two recent calculations using a perturbative-QCD approach predict splittings of $39 \pm 14 MeV / c^{2}$ [13] and $44 \pm 11 MeV / c^{2}$ [14], both being over two standard deviations away from the BABAR measurement. One can see that the recent BABAR result poses a serious challenge to theorists, which should spur renewed effort to improve calculations. More precise measurement of the $η_{b}$ mass would allow precision tests of lattice-QCD and perturbative-QCD calculations of the $Υ - η_{b}$ splitting.

The large amount of data that BABAR has accumulated on the $Υ (3 S)$ state should allow searches for other missing $b \bar{b}$ states. In particular, it may be possible to observe the $η_{b} (2 S)$ state via $M 1$ transitions. Many models predict the branching ratio to the $η_{b} (2 S)$ to be only a factor of 2 or 3 smaller than that to the $η_{b} (1 S)$ and therefore possibly observable. Other interesting possibilities consist of searching for the $h_{b} (1^{1} P_{1}$ ) in the processes $Υ (3 S) \to π^{0} h_{b} (1^{1} P_{1}) \to π^{0} γ η_{b}$ and the sequential process $Υ (3 S) \to π^{+} π^{-} h_{b} (1^{1} P_{1}) \to π^{+} π^{-} γ η_{b}$ [15]. The discovery of these states would represent an important step in completing the bottomonium spectrum and provide an important test of QCD-based models and calculations. Measurement of the hyperfine mass splittings between the triplet and singlet quarkonium states is crucial to understanding the role of spin-spin interactions in quarkonium models and in testing QCD calculations [7].

Acknowledgments

The author gratefully acknowledges Nathan Isgur and Jon Rosner for teaching him much of what he knows about this subject. This research was supported in part by the Natural Sciences and Engineering Research Council of Canada.

References

S. W. Herb et al., Phys. Rev. Lett. 39, 252 (1977)
W. Kwong, J. L. Rosner, and C. Quigg, Annu. Rev. Nucl. Part. Sci. 37, 325 (1987)
B. Aubert et al. (BABAR), Phys. Rev. Lett. 101, 071801 (2008)
A. Gray, I. Allison, C. T. H. Davies, E. Gulez, G. P. Lepage, J. Shigemitsu, and M. Wingate (HPQCD and UKQCD Collaborations), Phys. Rev. D 72, 094507 (2005)
E. Eichten and K. Gottfried, Physics Letters B 66, 286 (1977)
W. Celmaster, H. Georgi, and M. Machacek, Phys. Rev. D 17, 886 (1978)
N. Brambilla, et al. (Quarkonium Working Group), arXiv:hep-ph/0412158
J. L. Rosner et al. (CLEO Collaboration), Phys. Rev. Lett. 95, 102003 (2005)
S. Godfrey and N. Isgur, Phys. Rev. D 32, 189 (1985)
E. Eichten, S. Godfrey, H. Mahlke, and J. L. Rosner, arXiv:hep-ph/0701208
G. Bonvicini et al. (CLEO Collaboration), Phys. Rev. D 70, 032001 (2004)
S. Godfrey and J. L. Rosner, Phys. Rev. D 64, 074011 (2001); 65, 039901(E) (2002)
B. A. Kniehl, A. A. Penin, A. Pineda, V. A. Smirnov, and M. Steinhauser, Phys. Rev. Lett. 92, 242001 (2004)
S Recksiegel and Y. Sumino, Phys. Lett. B 578, 369 (2004)
S. Godfrey and J. L. Rosner, Phys. Rev. D 66, 014012 (2002)
W.-M. Yao et al., J. Phys. G: Nucl. Part. Phys. 33, 1 (2006)

About the Author

Stephen Godfrey received his B.A.Sc. from the University of Toronto in 1976, his M.Sc. from the Weizmann Institute in 1978, and his Ph.D. from the University of Toronto in 1983. He was a postdoctoral fellow at TRIUMF in Vancouver and at Brookhaven National Laboratory before becoming an Assistant Professor at the University of Guelph in 1987. He moved to Carleton University in Ottawa, Canada, in 1990 where he is currently a Professor of Physics. His research is in particle physics phenomenology, ranging from hadron spectroscopy to physics beyond the standard model at the LHC.