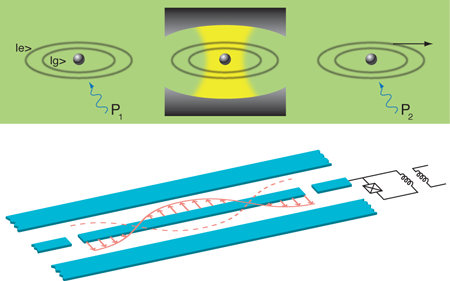
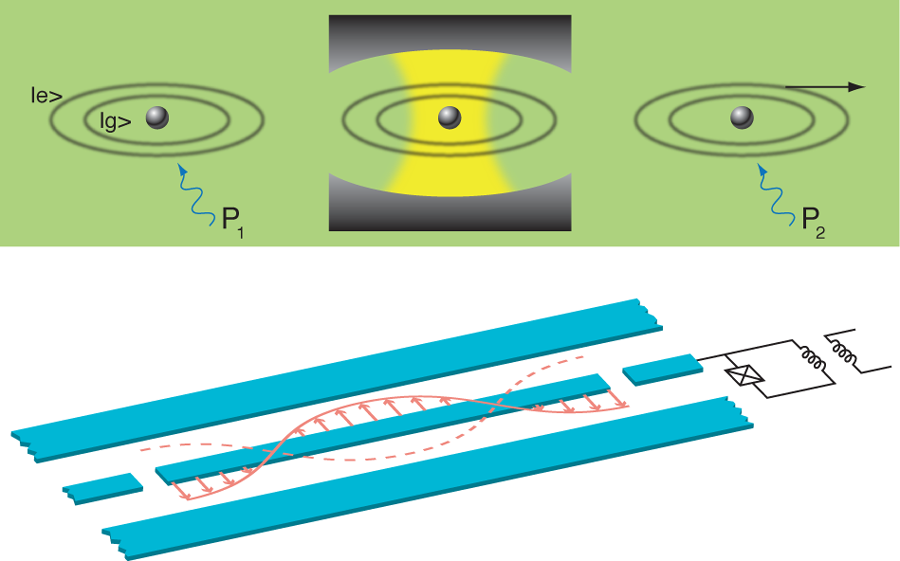
Filling a cavity with photons, and watching them leave

Alexandre Blais; Jay M. Gambetta

Viewpoint

Filling a cavity with photons, and watching them leave

Alexandre Blais

Département de Physique et Regroupement Québécois sur les Matériaux de Pointe, Université de Sherbrooke, Sherbrooke, Québec, Canada, J1K 2R1

Jay M. Gambetta

Institute for Quantum Computing and Department of Physics and Astronomy, University of Waterloo, Waterloo, Ontario, Canada, N2L 3G1

December 8, 2008• Physics 1, 39

Preparing a harmonic oscillator in a state with a well-defined energy is a tricky business. With the new tools provided by cavity and circuit quantum electrodynamics it is now possible to make these pure quantum states and watch how they evolve in time.

Figure caption — **Figure 1:** By coupling a nonlinear system, such as an atom, to the electromagnetic field, it is possible to create Fock states (eigenstates of the harmonic oscillator). (Top) Brune *et al.* send atoms (left) into a cavity (center). The atoms are prepared with pulse $P_{1}$ to be in a superposition of states $| e 〉$ and $| g 〉$ before they enter the cavity. The relative phase between these states, which is converted to probability amplitudes for $| e 〉$ and $| g 〉$ with pulse $P_{2}$ when the atoms exit the cavity, depends on the number of photons in the cavity. (Bottom) In place of a cavity, Wang *et al.* create an electromagnetic field in a microwave resonator (blue). A superconducting qubit, acting as an artificial atom, couples to the center conductor.

The harmonic oscillator is one of the most fundamental systems in quantum mechanics. Equipped with its solution—one of the first that every physics student learns to calculate exactly—it is possible to describe realistic problems, from phonons in a crystal to the interaction of light with an atom. It is perhaps ironic, then, how challenging it is to actually prepare a pure harmonic oscillator state with a well-defined excitation number $n$ , also known as a Fock state. Now, using different methods, two groups—Michel Brune and colleagues at the Laboratoire Kastler Brossel of the CRNS and Collège de France, both in Paris, and Haohua Wang and colleagues at the University of California in Santa Barbara (UCSB)—have created these nonclassical states of the harmonic oscillator and performed a detailed study of how they decay in time. The experiments, reported in Physical Review Letters [1,2] demonstrate that the lifetime of a Fock state with excitation number $n$ scales as $1 / n$ , as predicted by theory.

Since it is of relevance to both experiments, consider one of the simplest realizations of the harmonic oscillator: the electromagnetic field. Its excited states are photons and a Fock state corresponds to the creation of $n$ photons with the same energy, $ħ ω$ . However, when using a classical source with a well-defined frequency (such as a laser) to generate an electromagnetic field, the result is a coherent state: a superposition of Fock states that is nearly indistinguishable from a classical state. The reason is that the energy spectrum of the harmonic oscillator is linear, such that the energy provided by the source will spread over a wide distribution of Fock states. Instead, to directly prepare a purely nonclassical photon state and observe quantum effects, we need to make a sufficiently strong interaction between the electromagnetic field and an additional, nonlinear, component. This is the heart of the experiments from Brune et al. and Wang et al.

In the work from the CNRS group, the nonlinear components are atoms with excited states that are not evenly spaced in energy. In particular, they use circular Rydberg atoms (atoms in highly excited states and with maximum angular momentum: $l = | m | = n - 1$ ). These atoms have large dipole moments that couple strongly to the microwave photons that are used in the experiments. To enhance this coupling, the photons are confined to a cavity made out of two high-quality mirrors that face each other. The CNRS group has studied the interaction between light and matter in a cavity, also known as cavity quantum electrodynamics (QED) [3–5], with circular Rydberg atoms over the last 20 years. Thus, they have been able to carefully design the experiment so that the coupling strength between the circular Rydberg atoms and the photons in the cavity overwhelms all the decay rates of the combined system: the single-photon decay rate $κ$ out of the cavity, the atomic decay rate $Γ_{1}$ , and the atomic dephasing rate $Γ_{ϕ}$ . It is worth noting that cavities can now be fabricated with extremely large quality factors such that the single photon lifetime $1 / κ$ can be as large as 0.1 seconds [6]. This is long enough for photons to travel 39,000 km back and forth between the two mirrors separated by 2.7 cm!

The experiment by the CNRS group relies on the conditional preparation of Fock states. They first create a coherent state of the cavity field with a microwave source. Then, to prepare a pure but randomly chosen Fock state, they rely upon the magic of quantum measurements: they perform a measurement of photon number with result $n$ , which projects the classical field to the quantum state $| n 〉$ . The CNRS team’s measurement is special in the sense that it involves no energy exchange. In these so-called quantum nondemolition measurements, atoms that are nonresonant with the photons in the cavity are sent one by one across the cavity. Before entering the cavity, each atom is prepared in a superposition of two of its internal states, labeled $| g 〉$ and $| e 〉$ for ground and excited states (see Fig.1, top ). During the time that the atom is in the cavity, this superposition acquires a relative phase proportional to the number of photons in the cavity. After leaving the cavity, a second pulse converts this phase information to probability amplitudes for $| g 〉$ and $| e 〉$ , which are then measured by state-selective ionization of the atom. By repeating this process with sufficiently many atoms (roughly 110 in the experiment), the Fock state, which was randomly selected from the initial field distribution, is prepared with high accuracy.

After preparing the Fock state $| n 〉$ , every atom that is then sent through the cavity reveals information about the subsequent evolution of the cavity field. In this way, Brune et al. follow the time evolution of Fock states $n = 0$ through $n = 7$ , and can track how these states decay, something known as quantum process tomography. As expected from theory, they find that the decay rate of a Fock state with $n$ photons is $n κ$ , which is $n$ times faster than for a Fock state with $n = 1$ . This enhanced rate simply reflects the fact that each additional photon has its own probability to decay, speeding up the relaxation. Since in this experiment preparing a Fock state is a random process, completely characterizing the state is a costly enterprise, requiring up to a million single atom measurements.

In parallel, researchers have been developing an on-chip version of cavity QED, also known as circuit QED. In this system, the many Rydberg atoms are replaced by a single superconducting qubit and the cavity is a transmission-line resonator, essentially a one-dimensional superconducting coaxial cable (see Fig. 1, bottom). Gaps in the center conductor of the resonator play the role of the mirrors in cavity QED. Moreover, similarly to the cavity used by the CNRS group, excitations of the resonator are microwave photons. These essentially one-dimensional cavities have a small mode volume, resulting in a large electric field per photon. Superconducting qubits are electrical circuits based on Josephson junctions. With their well-defined energy levels, they behave as artificial atoms, providing the essential nonlinearity. In addition, superconducting qubits have a large effective dipole moment. As a result, this system can easily reach the strong coupling regime of cavity QED [7]. Groups at Yale [8] and Delft (in this last case using a different type of on-chip cavity) [9] first demonstrated strong coupling between a superconducting qubit and a microwave resonator in 2004. Because of the very strong coupling, it was predicted [10] and soon confirmed [11] that in circuit QED, Fock states could be resolved by measuring the qubit absorption spectrum. Earlier this year, the UCSB group showed they could prepare Fock states with up to $n = 6$ photons [12].

In the new experiments from the UCSB group [2], the superconducting qubit, playing the role of the atom, is capacitively coupled to the center conductor of the resonator (Fig. 1, bottom). An advantage of this artificial atom is that the energy difference between its $| g 〉$ and $| e 〉$ states can be tuned into and out of resonance with the resonator frequency. Starting with the qubit out of resonance and in its ground state $| g 〉$ , a classical source is used to pump it to $| e 〉$ . This energy quantum is then transferred to the resonator by tuning the qubit so it is in resonance with the microwave resonator for an appropriate amount of time. By repeating this process, Fock states with $n$ up to 15 have been created. The microwave resonator’s state can in turn be determined by tuning the qubit into resonance with the resonator and measuring the undriven Rabi oscillations of the qubit between $| g 〉$ and $| e 〉$ . Since the frequency of these oscillations depends characteristically on the photon number in the microwave resonator, Wang et al. can extract information about the photon distribution of the Fock state. Similarly to the CNRS group, they find that the $n$ -photon Fock state decays at the enhanced rate $n κ$ .

The experiments now reported by Brune et al. and Wang et al. go beyond the groups’ earlier work in that both are able to create Fock states with large $n$ and reach a level of precision with which to probe the decay of these states. By combining two prototypical systems—harmonic oscillators and two-level systems—cavity QED has established itself in the last 20 years as a unique test-bed for fundamental investigations of quantum mechanics. With the recent developments, such as cavities with high-quality factors and circuit QED, new ways to generate, control and measure non-classical states of light are now possible and more surprises are sure to be on their way.

References

M. Brune, J. Bernu, C. Guerlin, S. Deléglise, C. Sayrin, S. Gleyzes, S. Kuhr, I. Dotsenko, J. M. Raimond, and S. Haroche, Phys. Rev. Lett. 101, 240402 (2008)
H. Wang, M. Hofheinz, M. Ansmann, R. C. Bialczak, E. Lucero, M. Neeley, A. D. O’Connell, D. Sank, J. Wenner, A. N. Cleland, and J. M. Martinis, Phys. Rev. Lett. 101, 240401 (2008)
S. Haroche and J.-M. Raimond, Exploring the quantum: atoms, cavities and photons (Oxford University Press, Oxford, 2006)
H. Mabuchi and A. C. Doherty, Science 298, 1372 (2002)
R. Miller, T. E. Northup, K. M. Birnbaum, A. Boca, A. D. Boozer, and H. J. Kimble, J. Phys. B 38, S551 (2005)
S. Gleyzes, S. Kuhr, C. Guerlin, J. Bernu, S. Deleglise, U. Busk Hoff, M. Brune, J.-M. Raimond, and S. Haroche, Nature 446, 297 (2007)
A. Blais, R. S. Huang, A. Wallraff, S. M. Girvin, and R. J. Schoelkopf, Phys. Rev. A 69, 062320 (2004)
A. Wallraff, D. I. Schuster, A. Blais, L. Frunzio, R. S. Huang, J. Majer, S. Kumar, S. M. Girvin, and R. J. Schoelkopf, Nature 431, 162 (2004)
I. Chiorescu, P. Bertet, K. Semba, Y. Nakamura, C. J. P. M. Harmans, and J. E. Mooij, Nature 431, 159 (2004)
J. Gambetta, A. Blais, D. I. Schuster, A. Wallraff, L. Frunzio, J. Majer, M. H. Devoret, S. M. Girvin, and R. J. Schoelkopf, Phys. Rev. A 74, 042318 (2006)
D. I. Schuster, A. A. Houck, J. A. Schreier, A. Wallraff, J. M. Gambetta, A. Blais, L. Frunzio, J. Majer, B. Johnson, M. H. Devoret, S. M. Girvin, and R. J. Schoelkopf, Nature 445, 515 (2007)
M. Hofheinz, E. M. Weig, M. Ansmann, R. C. Bialczak, E. Lucero, M. Neeley, A. D. O’Connell, H. Wang, J. M. Martinis, and A. N. Cleland, Nature 454, 310 (2008)

About the Authors

Alexandre Blais is an Associate professor of theoretical physics in the Department of Physics at the Université de Sherbrooke, Québec Canada. After receiving his Ph.D. from the Université de Sherbrooke in 2002, he worked as a postdoctoral researcher at Yale University (2003–2005). His research interests are at the intersection of nanophysics and quantum optics, and focus on superconducting qubits and circuit quantum electrodynamics. He is a fellow of the Quantum Information Science and the Quantum Materials programs of the Canadian institute for advanced research.

Jay M. Gambetta received his B.Sc. (Hons.) (2000) and Ph.D. (2004) in theoretical physics at Griffith University, Australia. From 2004 to 2007 he worked as a Postdoctoral Associate at Yale University and is currently a Postdoctoral Fellow at the Institute for Quantum Computing at the University of Waterloo, Canada. His main research interests include superconducting qubits, quantum optics, measurement theory, and quantum computation.