How Casimir forces are shaping up

Steve K. Lamoreaux

Viewpoint

How Casimir forces are shaping up

Department of Physics, Yale University, New Haven, CT 06520-8120.

July 14, 2008• Physics 1, 4

Modification of electromagnetic zero-point fluctuations by closely spaced conductors causes an interaction between them called the Casimir force. New experiments with nanostructured silicon substrates show that the geometry of the conducting surfaces has a large effect on this force.

Figure caption — **Figure 1:** (Upper left) A nanostructured silicon surface is used as one plate in a Casimir experiment. The structure dimensions are chosen to affect the electromagnetic modes that contribute most to the Casimir force at distances on the order of a few 100 nm. (Upper right) Schematic of the experiment, partially to scale. The gradient of the force is measured through a change in oscillation frequency of a micromechanical torsion oscillator fabricated from silicon (shown in bottom micrograph) as the distance between the upper sphere and the nanostructured surface is changed. The lower sphere serves as a simple mechanical spacer.

The last great fundamental discovery in quantum mechanics was made in 1948 by Hendrik B. G. Casimir [1]. This discovery, the so-called Casimir effect, is the theoretical prediction that two closely spaced plane-parallel mirrors will be mutually attracted due to the modification of the electromagnetic mode structure between the mirrors. This attractive force comes about from the zero-point energy associated with the modes; the total energy decreases as the plates are brought together. As this force is due to zero-point energy, the force persists even at absolute zero temperature. This effect has been experimentally demonstrated many times, and the fundamental theory appears sound, at least for the simple systems that have been studied. Now, in a paper published in Physical Review Letters [2], Chan et al. at the University of Florida and Bell Laboratories, go beyond plane parallel surfaces and show how more complex surface geometry can influence the Casimir effect. This may bear directly on the extent to which Casimir forces contribute to the behavior of micro- and nanomechanical systems.

The original discovery of the Casimir effect is more fundamental than one might expect: Every quantum field has a zero-point energy, so any system that has accessible states governed by external boundary conditions will have a Casimir-like contribution to its energy. For example, there is a Casimir-like contribution to the energy of quarks bound in a nucleus as a described in the bag model due to boundary that is introduced in this model. These effects and others are well described in the book by Milton [3].

Casimir himself attempted to apply his namesake force to one of the simplest of the elementary particles, the electron. Casimir modeled the electron as a conducting ball of uniform charge that would contract due to the zero-point energy of the external electromagnetic modes. This contractive force would be balanced by the space-charge repulsion of the uniform charge density, when the conducting sphere of constant total charge was just the right diameter. The fine structure constant $α \approx 1 / 137$ , which relates to the electron diameter, could then be determined from fundamental parameters along with a calculation of how the electromagnetic mode zero-point energy changes as the sphere contracts [4].

So compelling was this possibility of determining the fine structure constant that Boyer did the calculation of the spherical mode problem [5]. He found that the Casimir force, or stress, due to the conducting sphere modes, causes the sphere to expand. Thus Casimir’s lovely model fails. Boyer’s result was interesting enough that it led to the exploration of the effects of geometry on the Casimir force. It has been shown, for example, that for rectangular bodies, the sign and magnitude of the stress depends on the aspect ratio of the rectangle.

Until now, no significant or nontrivial corrections to the Casimir force due to boundary conditions have been observed experimentally. The form of boundary deformations so far considered, together with the accuracy and precision of experimental studies, have been adequately theoretically described by straightforward geometrical averaging. For the systems that had previously been considered, it is not clear that an experimental measurement of the external stress is even possible. Cutting a sphere in half clearly changes the boundary value problem; it is unlikely that the two halves of such a sliced sphere will be repelled with a force that is given by the external stress on the unsliced sphere.

However, there are other possible ways to generate a geometrical influence on the Casimir force. A conceptually straightforward way is to contour the surfaces of the plates at a length scale comparable to the mode wavelengths that contribute most to the net Casimir force. For a plate separation $z$ , the wavelengths that contribute most are $\approx π z$ . This means that a surface nanopatterned at 400 nm level should show significant geometrical effects for separations below 1 µm. Indeed, the work of Chan et al. has produced a convincing measurement of a nontrivial geometrical influence on the Casimir force [2].

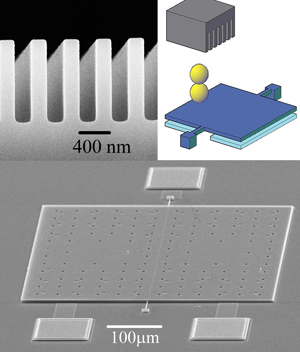
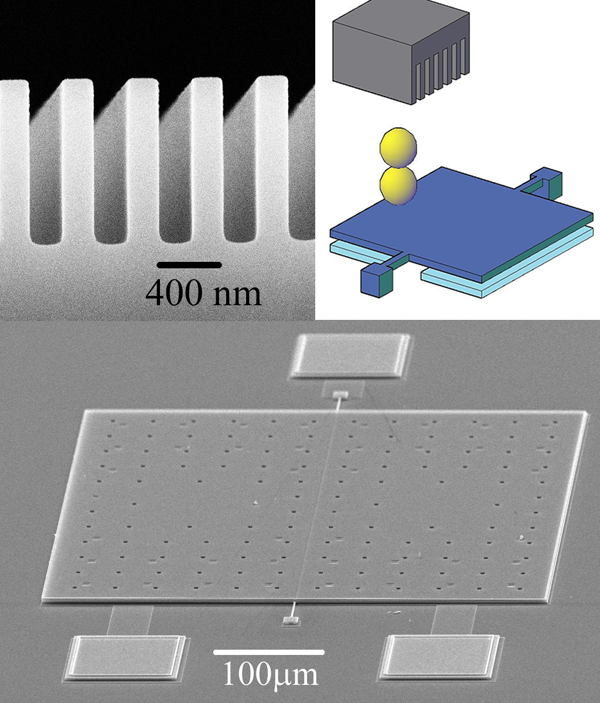
These measurements, between a nanostructured silicon surface (upper left panel of Fig. 1) and a gold sphere, were made using a micromechanical torsional oscillator (upper right panel of Fig. 1). The change in resonant frequency of the oscillator, as a function of separation between the sphere and the surface, provided a measure of the gradient of the Casimir force. The gold sphere, actually a glass sphere of radius 50 µm coated with 400 nm of gold, was attached to one side of the oscillator that comprised a 3.5 µm thick, 500 µm square silicon plate suspended by two tiny torsion rods. The sphere–oscillator assembly was moved toward the nanostructured surface by use of a piezoelectric actuator.

Two different nanostructured plates, compared with a smooth plate, were measured in this work. The geometry of the nanostructures—rectangular trenches etched in the surface of highly p-doped silicon—were chosen because the effects are expected to be large in such a geometry. Previously, Büscher and Emig had calculated the effective modification of the Casimir force due to such a geometry, but for the case of perfect conductors [6]. Even though the calculations were not for real materials, these theoretical results appeared as a reasonable starting point for a comparison with an experiment.

Casimir’s calculation addressed perfectly conducting plates. The theory of the force was subsequently generalized by Lifshitz to real materials at finite temperature in his seminal 1956 paper [7]. Although much progress has recently been made toward a realistic and believable accuracy and precision with which the Casimir force can be calculated for real materials [8], problems associated with the well-known experimental variability of sputtered or evaporated films were avoided in the work of Chan et al. by comparing two different nanostructured plates with a smooth plate, all made from the same silicon substrate, and all using the same gold-sphere–oscillatory assembly.

The geometric modification of the Casimir force was detected by measuring a deviation from that expected by use of the so-called proximity force approximation (PFA), or the pairwise additive approximation (PAA). Briefly, the PFA was introduced in relation to the Casimir force by Derjaguin in 1957 [9] to describe the force between curved surfaces, and this approximation is known to be extremely accurate when the curvature is much less than the separation between the surfaces. Indeed, the use of a sphere and a flat plate vastly simplifies the experiment because the system is fully mechanically defined in terms of the point of closest approach and the radius of curvature of the sphere. For two flat plates the system is specified by two tilt angles, the areas, long-scale smoothness, and a separation, which all need to be defined, measured, and controlled—a daunting problem, particularly when small deviations of the force are being measured.

The success of the PFA is so good that it suggests a means of detecting a geometrical effect. Basically, the surface is divided into infinitesimal units, and it is assumed that the total force can be determined by adding the Casimir force, appropriately scaled by area, between surface unit pairs in opposite surfaces; this is the PAA. Thus, for the nanostructured surfaces used by Chan et al., roughly a 50% reduction in force would be expected by the PAA, because the very deep trenches (depth $t = 2 a \approx 1 μ m$ ), etched as a regular array, were designed to etch away about half of the surface, and this fraction was carefully measured. As mentioned, two different trench spacings, $λ$ , were fabricated and measured, such that $λ / a = 1.87$ (sample A) and 0.82 (sample B), and were compared to a smooth surface. The Casimir force between the gold sphere and the smooth plate, as calculated from the tabulated properties of gold and silicon, taking into account the conductivity due to the doping, agree with the experimental results to about 10% accuracy. For sample A, the force is 10% larger than expected by the PAA, as evaluated by use of the measured smooth-surface force, and for sample B, it is 20% larger, in the range $150 < z < 250$ nm. The deviation increases as $λ / a$ decreases, as expected.

The theory of Büscher and Emig predicts deviations from the PAA twice as large as were observed. Nonetheless, the results of Chan et al. indicate a clear effect of geometry on the Casimir force in the clear deviation from the PAA. This deviation was detectable through the experimental trick of comparing different aspect ratio trenches to a smooth surface in otherwise identical materials. So even though ab initio calculation of the Casimir force for a real material using tabulated optical properties cannot be accurate to better than 10%, this problem was simply circumvented by the comparison technique.

Much theoretical work remains to be done toward gaining a complete understanding of the experimental observations. The already difficult calculations are made more so by the finite conductivity effects of the plates, and the real smoothed shape of the trenches as opposed to ideal sharp features. However, the creativity of theorists on this subject appears limitless, as does the numerical computing power offered by even a modest cluster of computers for problems of this type. We can expect that in the near future the discrepancy between theory and experiment will be resolved; the excitement of further efforts lie in the possibility that our understanding of the Casimir force is incomplete in a significant way.

References

H. B. G. Casimir, Proc. Kon. Ned. Akad. Wetenschap51, 793 (1948)
H. B. Chan, Y. Bao, J. Zou, R. A. Cirelli, F. Klemens, W. M. Mansfield, and C. S. Pai, Phys. Rev. Lett. 101, 030401 (2008)
K. A. Milton, The Casimir Effect: Physical Manifestations of Zero-Point Energy (World Scientific, New Jersey, 2001) [Amazon][WorldCat].
P. W. Milonni, The Quantum Vacuum (Academic Press, San Diego, 1994), pp. 286-288. [Amazon][WorldCat].
T. H. Boyer, Phys. Rev. 174, 1764 (1968)
R. Büscher and T. Emig, Phys. Rev. A 69, 062101 (2004)
E. M. Lifshitz, Sov. Phys. JETP 2, 73 (1956)
V. B. Svetovoy, P. J. van Zwol, G. Palasantzas, and J. T. M. De Hosson, Phys. Rev. B 77, 035439 (2008)
B. V. Derjaguin and I. I. Abrikosova, Sov. Phys. JETP 3, 819 (1957)

About the Author

Steve K. Lamoreaux received his Ph.D. in atomic physics from the University of Washington in 1986, where he worked until 1996 at which time he moved to Los Alamos National Laboratory. In 2006, he assumed a faculty position in the Department of Physics at Yale. While at the University of Washington, he performed a high precision Casimir force experiment, the result of a series of undergraduate research projects, using a torsion pendulum.