Theory for 1D Quantum Materials Tested with Cold Atoms and Superconductors
One-dimensional (1D) materials—from nanowires to carbon nanotubes to linear arrays of cold atoms—hold promise for applications in nanoelectronics, sensing, energy harvesting, and quantum information processing. They are also ideal for exploring fundamental quantum phenomena at the nanoscale. Their theoretical description relies on a model known as the Tomonaga-Luttinger liquid (TLL) [1], which can account for the many-body interactions within a 1D ensemble of quantum systems (fermions, spins, or bosons). To date, however, only a few of the aspects of this theory have been experimentally tested. This is mostly due to the difficulty of realizing an ideal and controllable 1D system experimentally.
Two independent teams have now carried out some of the most detailed tests to date of TLL theory. Bing Yang, at the University of Science and Technology of China in Hefei, and co-workers have shown TLL behavior in a 1D array of cold atoms [2], establishing cold atoms as a reliable platform for simulating some aspects of TLL physics that might be hard to access in condensed-matter systems. Timothy Duty of the University of New South Wales, Australia, and co-workers have tested TLL predictions in a 1D array of Josephson junctions [3]—a system that allows them to study the effects of disorder on TLL physics.
Understanding the effects of many-body interactions in quantum systems is a long-standing challenge. In most cases, describing ∼1023coupled degrees of freedom (the approximate number of electrons in a cubic centimeter of material) is an intractable problem. Simplifying approaches exist in 2 and 3 dimensions for both bosonic and fermionic systems. For bosonic systems, mean-field approximations convert a many-body problem into a one-body one: each boson interacts with the averaged field of the others. And fermionic systems can be described by Lev Landau’s Fermi-liquid theory, which recasts the problem of strongly interacting particles in terms of excitations (called Landau quasiparticles) that are nearly free, bringing us back to the more comfortable case of free particles. Unfortunately, the game changes in 1D, as all of the above descriptions break down.
The key difference between 1D systems and higher-dimensional systems is that the former are governed by collective excitations, not individual ones. This fact can be illustrated by the queuing of people in a line: an individual can only move together with his or her neighbors. The TLL formalism rests on the fact that only two parameters are sufficient to describe the system: the speed of collective excitations (such as oscillations of the density of particles, or sound waves propagating through the system) and the TLL parameter (which measures the degree of quantum fluctuations inside the material). TLL theory predicts certain hallmark features: superconductivity, quasi-long-range order at zero temperature, and the tendency of the system to undergo instabilities—such as charge- or spin-density waves [1].
However, the observation of TTL features has been a long-standing challenge, with the first hints found in condensed-matter systems. With the advent of cold atoms as condensed-matter simulators, researchers had hoped to find easier ways to observe TLL physics. But there are complications due to the finite size of the systems, the difficulty of reaching sufficiently low temperatures to reach quantum regimes and, most importantly, the challenge of realizing homogeneous 1D systems—the confining potential of the traps used to hold the atoms leads to an atomic density varying from point to point. Such an inhomogeneity enormously complicates the theoretical description of the system. (See Refs. [1] and [4] for a review of TLL studies in both condensed matter and cold atoms.)
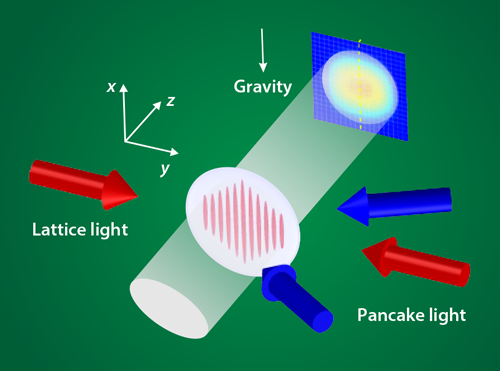
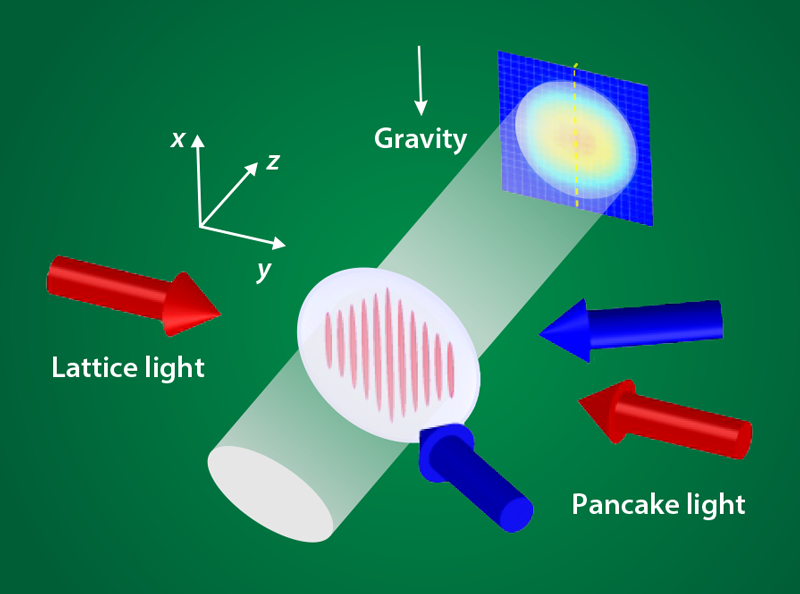
Yang and colleagues circumvent some of these difficulties using a clever experimental setup based on 1D arrays of laser-trapped, ultracold rubidium-87 atoms (see Fig. 1). Using a resonant light pulse, they remove atoms from the middle of the arrays, generating a density oscillation that moves outwards from the center of the array. Since the atoms are confined in the harmonic potential created by the trapping laser beams, the atom density is nearly uniform at the center of the array, which can be regarded, to a good approximation, as a homogeneous system. This setup allowed them to precisely determine the velocity by which sound waves triggered by the density perturbation propagate in the system. From the sound velocity and the density, they extracted the TLL parameter. Finally, they compared TLL predictions with experimental data on the atoms’ momentum distribution. The good agreement between theory and experiments showed that TLL provides an excellent description of this 1D bosonic system.
Meanwhile, Duty and his co-workers test TLL behavior in a wildly different system—a 1D array of superconducting Josephson junctions (see Fig. 2). The disorder introduced during the fabrication of this device leads to slight charge differences on each junction and thus to a disordered bosonic system (where the “bosons’’ are the Cooper pairs in the superconductors). This system thus offers a unique controllable platform for testing how disorder affects TTL physics.
Understanding the impact of disorder on a 1D quantum system is challenging. If the interactions can be neglected, we know that even an infinitesimal degree of disorder would lead to the celebrated Anderson localization [5]: interference effects between the electrons’ wave functions halt the diffusion of electrons, and the system becomes fully insulating. But what happens to the system when interactions compete with disorder is less clear. Naively, if strong interactions lead to a collective quantum state (for bosons, a superfluid state; for fermions, a superconducting state), one would expect such a state to be immune to disorder. However, theoretical studies in 1D [6] and higher dimensions [7] showed that, in the case of bosons, the disorder–interaction competition leads to a transition between two phases: a superfluid in which interactions wash out the disorder, and a Bose glass—a many-body insulating (localized) phase whose lack of lattice order is reminiscent of a glass. Features of this phase transition have been previously seen in several systems. However, it has proven difficult to carry out quantitative tests of the critical behavior at the transition because that would require both good homogeneity and low temperatures (which are easier to achieve in solid-state systems) and control of the interaction strength or disorder (easier in cold atomic systems).
In this respect, Duty’s device features the advantages of a solid-state system while offering the possibility of controlling interaction strength. By varying the sizes of the junctions, the authors were able to scan through the phase transition. From the charge on the junctions and their Josephson energies, they derived the TLL parameter needed for the description of such a system. Measurements of the critical voltage—the threshold voltage at which current can circulate in the array—as a function of the parameters of the device revealed that disorder controls a transition between a superfluid and an insulator with clear signatures of a Bose glass state. The observed scaling of the critical voltage as well as the critical behavior predicted by TTL [6] were in excellent agreement with theoretical expectations.
By providing a remarkable experimental demonstration of several so-far-elusive aspects of TLL theory, these two new studies confirm that TLL theory now plays the same key role in 1D systems that Fermi-liquid theory plays in our understanding of 2D and 3D condensed-matter systems. Without a doubt, this research will open new chapters in the TLL field by inspiring studies that examine how other perturbations (coupling between different 1D chains, spin-orbit coupling, and the like) can lead to novel and potentially exotic states in 1D materials.
This research is published in Physical Review Letters.
Correction (23 October 2017): An earlier version of the article incorrectly stated that the figures had been adapted from figures by Philip Krantz of Krantz NanoArt. They were in fact adapted from Refs. [2, 3].
References
- The TTL theory was developed in the 1980s by physicist Frederick Duncan Haldane: F. D. M. Haldane, “General Relation of Correlation Exponents and Spectral Properties of One-Dimensional Fermi Systems: Application to the Anisotropic S=1∕2 Heisenberg Chain,” Phys. Rev. Lett. 45, 1358 (1980); “Effective Harmonic-Fluid Approach to Low-Energy Properties of One-Dimensional Quantum Fluids,” 47, 1840 (1981), building on earlier work in the 1970s; T. Giamarchi, Quantum Physics in one Dimension, International Series of Monographs on Physics Vol. 121 (Oxford University Press, Oxford, 2004)[Amazon][WorldCat]; M. A. Cazalilla, R. Citro, T. Giamarchi, E. Orignac, and M. Rigol, “One Dimensional Bosons: From Condensed Matter Systems to Ultracold Gases,” Rev. Mod. Phys. 83, 1405 (2011), and references therein.
- B. Yang et al., “Quantum Criticality and the Tomonaga-Luttinger Liquid in One-Dimensional Bose Gases,” Phys. Rev. Lett. 119, 165701 (2017).
- K. Cedergren, R. Ackroyd, S. Kafanov, N. Vogt, A. Shnirman, and T. Duty, “Insulating Josephson-Junction Chains as Pinned Luttinger Liquids,” Phys. Rev. Lett. 119, 167701 (2017).
- T. Giamarchi, “One-dimensional Physics in the 21st Century,” C. R. Acad. Sci. 17, 322 (2016).
- P. W. Anderson, “Absence of Diffusion in Certain Random Lattices,” Phys. Rev. 109, 1492 (1958).
- T. Giamarchi and H. J. Schulz, “Anderson Localization and Interactions in One-Dimensional Metals,” Phys. Rev. B 37, 325 (1988).
- M. P. A. Fisher, P. B. Weichman, G. Grinstein, and D. S. Fisher, “Boson Localization and the Superfluid-Insulator Transition,” Phys. Rev. B 40, 546 (1989).