Searching for Order in Turbulent Flow
Most of us associate turbulence with a bumpy ride on a plane. Yet turbulent flow is practically everywhere, even if we aren’t aware of it. The air we exhale, the blood pumped through our bodies’ ascending aorta, and the steam rising from a hot cup of coffee are all in turbulent motion. Even if we could see these flows, it would be difficult to discern any order in the whirling currents that they contain. A group led by Michael Schatz at the Georgia Institute of Technology in Atlanta has now shown with experiments and simulations that flow patterns with a surprising amount of order can underlie turbulent flow [1], at least when the turbulence is weak. Having identified these ordered structures in the lab, they were able to predict the evolution of a turbulent flow, which had previously been difficult to do.
There is no short answer to the question “What is turbulence?” In contrast to the well-ordered laminar flow that prevails at low flow speeds, turbulence is disordered and fluctuating, and it contains whirls of many different sizes that exchange energy with one another. As such, turbulence has proven extremely difficult to describe from first principles. Although the Navier-Stokes equations governing fluid flow are well known, their nonlinear nature means that they can only be solved in exceptional cases (such as laminar pipe flow). Thus there is little hope to obtain an expression that would encompass the complex spatiotemporal dynamics of turbulence. Researchers have therefore largely described turbulence in statistical terms, focusing on deriving averaged quantities and scaling relationships, such as that between the amount of energy in an eddy and its size.
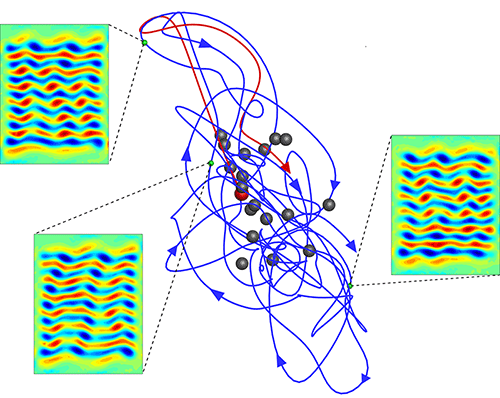
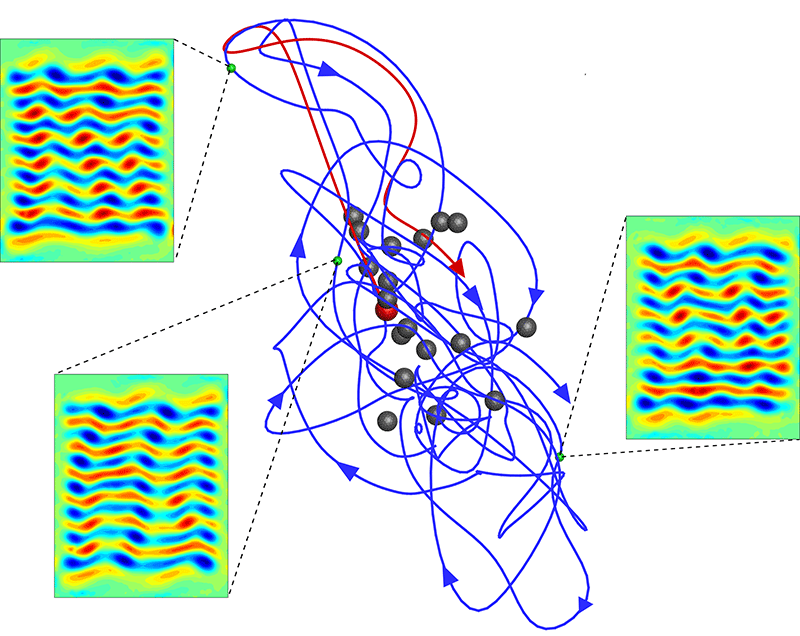
A different tack that has become increasingly popular [2–5], and the one that Schatz and co-workers follow, is to view fluid flow as a dynamical system, whose possible states lie in a high-dimensional space [6]. In this framework, the time evolution of a flow’s velocity field is represented by a trajectory through state space, in which each point corresponds to a solution to the Navier-Stokes equations. Here, laminar flow is a fixed point (an equilibrium solution) in state space, whereas turbulent flow is a chaotic trajectory. This chaotic motion takes place in a region of state space that accommodates infinitely many unstable periodic orbits and unstable equilibrium points, collectively known as exact coherent structures (ECS). Each of these structures is flanked by stable and unstable manifolds: bundles of trajectories that approach and leave, respectively, the vicinity of an ECS. A turbulent trajectory continuously bounces from one unstable solution to another (Fig. 1): it is attracted by the stable manifold of an equilibrium point, where the fluid’s dynamics slows down and its velocity field resembles that of the equilibrium state; it then leaves this region along the unstable manifold and heads to another ECS, and so forth. The benefit of this state-space picture is that it provides a way to predict the future of a flow from its instantaneous position by using the “catalog” of ECS and their stable and unstable manifolds.
It was by looking for flow patterns associated with a slow down in dynamics that Schatz and co-workers were able to identify ordered structures in a turbulent liquid. The team worked with a shallow layer of electrolytic fluid inside a small box, using a combination of electric and magnetic fields to jostle the fluid just enough for a weak amount of turbulence to set in. To determine this 2D fluid’s velocity field, the team suspended particles in the electrolyte and imaged them at different times. They then compared patterns in the fluid that were measured when the fluid’s dynamics slowed down with computer-simulated patterns corresponding to unstable equilibrium solutions. They found a close match between the measured and simulated patterns.
This agreement allowed the researchers to take their study to a predictive level. For one, they demonstrated that weakly turbulent flow follows the unstable manifold of an ECS structure as it leaves its neighborhood. They also confirmed that the flow bounces between unstable solutions, as expected. In sum, the authors have shown that once they know the ECS for a given experimental setting, and the stable and unstable manifolds associated with these ECS, they can use these solutions as a predictive tool—a marked step beyond the purely statistical approach to describing turbulence.
Earlier studies [7–9] of turbulence in shear flows have found evidence that turbulent flows visit equilibrium solutions. But the evidence from the experiments by Schatz and colleagues is particularly convincing. This can largely be attributed to their decision to study a 2D system, in which the particle positions can be measured with high accuracy, and to focus on very weak turbulence, which makes the comparison between experiment and simulations more reliable. The natural next steps would be to ascertain if this predictability is possible in 3D flows and at higher Reynolds numbers, where flows are truly turbulent and contain whirls and eddies of many different sizes. Such steps would be challenging, as they may entail ECS of higher dimensionality than the ones the authors studied, such as periodic orbits and tori, which are both more difficult to calculate and observe.
This research is published in Physical Review Letters.
References
- B. Suri, J. Tithof, R. O. Grigoriev, and M. F. Schatz, “Forecasting Fluid Flows Using the Geometry of Turbulence,” Phys. Rev. Lett. 118, 114501 (2017).
- R. R. Kerswell, “Recent Progress in Understanding the Transition to Turbulence in a Pipe,” Nonlinearity 18, R17 (2005).
- B. Eckhardt, T. M. Schneider, B. Hof, and J. Westerweel, “Turbulence Transition in Pipe Flow,” Ann. Rev. Fluid Mech. 39, No. 1, 447 (2007).
- J. F. Gibson, J. Halcrow, and P. Cvitanović, “Visualizing the Geometry of State Space in Plane Couette Flow,” J. Fluid Mech. 611, 107 (2008).
- G. Kawahara, M. Uhlmann, and L. van Veen, “The Significance of Simple Invariant Solutions in Turbulent Flows,” Ann. Rev. Fluid Mech. 44, 203 (2012).
- E. Hopf, “A Mathematical Example Displaying Features of Turbulence,” Comm. Pure Appl. Math. 1, 303 (1948).
- B. Hof, “Experimental Observation of Nonlinear Traveling Waves in Turbulent Pipe Flow,” Science 305, 1594 (2004).
- A. de Lozar, F. Mellibovsky, M. Avila, and B. Hof, “Edge State in Pipe Flow Experiments,” Phys. Rev. Lett. 108, 214502 (2012).
- D. J. C. Dennis and F. M. Sogaro, “Distinct Organizational States of Fully Developed Turbulent Pipe Flow,” Phys. Rev. Lett. 113, 234501 (2014).